Erratum for “An inverse theorem for the Gowers U^{s+1}[N]-norm”

The purpose of this post is to report an erratum to the 2012 paper “An inverse theorem for the Gowers -norm” of Ben Green, myself, and Tamar Ziegler (previously discussed in this blog post). The main results of this paper have been superseded with stronger quantitative results, first in work of Manners (using somewhat different methods), and more recently in a remarkable paper of Leng, Sah, and Sawhney which combined the methods of our paper with several new innovations to obtain quite strong bounds (of quasipolynomial type); see also an alternate proof of our main results (again by quite different methods) by Candela and Szegedy. In the course of their work, they discovered some fixable but nontrivial errors in our paper. These (rather technical) issues were already implicitly corrected in this followup work which supersedes our own paper, but for the sake of completeness we are also providing a formal erratum for our original paper, which can be found here. We thank Leng, Sah, and Sawhney for bringing these issues to our attention.

Excluding some minor (mostly typographical) issues which we also have reported in this erratum, the main issues stemmed from a conflation of two notions of a degree filtration

of a group , which is a nested sequence of subgroups that obey the relation for all . The weaker notion (sometimes known as a prefiltration) permits the group to be strictly smaller than , while the stronger notion requires and to equal. In practice, one can often move between the two concepts, as is always normal in , and a prefiltration behaves like a filtration on every coset of (after applying a translation and perhaps also a conjugation). However, we did not clarify this issue sufficiently in the paper, and there are some places in the text where results that were only proven for filtrations were applied for prefiltrations. The erratum fixes this issues, mostly by clarifying that we work with filtrations throughout (which requires some decomposition into cosets in places where prefiltrations are generated). Similar adjustments need to be made for multidegree filtrations and degree-rank filtrations, which we also use heavily on our paper.

In most cases, fixing this issue only required minor changes to the text, but there is one place (Section 8) where there was a non-trivial problem: we used the claim that the final group was a central group, which is true for filtrations, but not necessarily for prefiltrations. This fact (or more precisely, a multidegree variant of it) was used to claim a factorization for a certain product of nilcharacters, which is in fact not true as stated. In the erratum, a substitute factorization for a slightly different product of nilcharacters is provided, which is still sufficient to conclude the main result of this part of the paper (namely, a statistical linearization of a certain family of nilcharacters in the shift parameter ).

Again, we stress that these issues do not impact the paper of Leng, Sah, and Sawhney, as they adapted the methods in our paper in a fashion that avoids these errors.

Notes on the B+B+t theorem

A recent paper of Kra, Moreira, Richter, and Robertson established the following theorem, resolving a question of Erdös. Given a discrete amenable group , and a subset of , we define the Banach density of to be the quantity

where the supremum is over all Følner sequences of . Given a set in , we define the restricted sumset to be the set of all pairs where are distinct elements of .

Theorem 1 Let be a countably infinite abelian group with the index finite. Let be a positive Banach density subset of . Then there exists an infinite set and such that .

Strictly speaking, the main result of Kra et al. only claims this theorem for the case of the integers , but as noted in the recent preprint of Charamaras and Mountakis, the argument in fact applies for all countable abelian in which the subgroup has finite index. This condition is in fact necessary (as observed by forthcoming work of Ethan Acklesberg): if has infinite index, then one can find a subgroup of of index for any that contains (or equivalently, is -torsion). If one lets be an enumeration of , and one can then check that the set

has positive Banach density, but does not contain any set of the form for any (indeed, from the pigeonhole principle and the -torsion nature of one can show that must intersect whenever has cardinality larger than ). It is also necessary to work with restricted sums rather than full sums : a counterexample to the latter is provided for instance by the example with and . Finally, the presence of the shift is also necessary, as can be seen by considering the example of being the odd numbers in , though in the case one can of course delete the shift at the cost of giving up the containment .

Theorem 1 resembles other theorems in density Ramsey theory, such as Szemerédi’s theorem, but with the notable difference that the pattern located in the dense set is infinite rather than merely arbitrarily large but finite. As such, it does not seem that this theorem can be proven by purely finitary means. However, one can view this result as the conjunction of an infinite number of statements, each of which is a finitary density Ramsey theory statement. To see this, we need some more notation. Observe from Tychonoff’s theorem that the collection is a compact topological space (with the topology of pointwise convergence) (it is also metrizable since is countable). Subsets of can be thought of as properties of subsets of ; for instance, the property a subset of of being finite is of this form, as is the complementary property of being infinite. A property of subsets of can then be said to be closed or open if it corresponds to a closed or open subset of . Thus, a property is closed and only if if it is closed under pointwise limits, and a property is open if, whenever a set has this property, then any other set that shares a sufficiently large (but finite) initial segment with will also have this property. Since is compact and Hausdorff, a property is closed if and only if it is compact.

The properties of being finite or infinite are neither closed nor open. Define a smallness property to be a closed (or compact) property of subsets of that is only satisfied by finite sets; the complement to this is a largeness property, which is an open property of subsets of that is satisfied by all infinite sets. (One could also choose to impose other axioms on these properties, for instance requiring a largeness property to be an upper set, but we will not do so here.) Examples of largeness properties for a subset of include:

• has at least elements.
• is non-empty and has at least elements, where is the smallest element of .
• is non-empty and has at least elements, where is the element of .
• halts when given as input, where is a given Turing machine that halts whenever given an infinite set as input. (Note that this encompasses the preceding three examples as special cases, by selecting appropriately.)

We will call a set obeying a largeness property an -large set.

Theorem 1 is then equivalent to the following “almost finitary” version (cf. this previous discussion of almost finitary versions of the infinite pigeonhole principle):

Theorem 2 (Almost finitary form of main theorem) Let be a countably infinite abelian group with finite. Let be a Følner sequence in , let , and let be a largeness property for each . Then there exists such that if is such that for all , then there exists a shift and contains a -large set such that .

Proof of Theorem 2 assuming Theorem 1. Let , , be as in Theorem 2. Suppose for contradiction that Theorem 2 failed, then for each we can find with for all , such that there is no and -large such that . By compactness, a subsequence of the converges pointwise to a set , which then has Banach density at least . By Theorem 1, there is an infinite set and a such that . By openness, we conclude that there exists a finite -large set contained in , thus . This implies that for infinitely many , a contradiction.

Proof of Theorem 1 assuming Theorem 2. Let be as in Theorem 1. If the claim failed, then for each , the property of being a set for which would be a smallness property. By Theorem 2, we see that there is a and a obeying the complement of this property such that , a contradiction.

Remark 3 Define a relation between and by declaring if and . The key observation that makes the above equivalences work is that this relation is continuous in the sense that if is an open subset of , then the inverse image

is also open. Indeed, if for some , then contains a finite set such that , and then any that contains both and lies in .

For each specific largeness property, such as the examples listed previously, Theorem 2 can be viewed as a finitary assertion (at least if the property is “computable” in some sense), but if one quantifies over all largeness properties, then the theorem becomes infinitary. In the spirit of the Paris-Harrington theorem, I would in fact expect some cases of Theorem 2 to undecidable statements of Peano arithmetic, although I do not have a rigorous proof of this assertion.

Despite the complicated finitary interpretation of this theorem, I was still interested in trying to write the proof of Theorem 1 in some sort of “pseudo-finitary” manner, in which one can see analogies with finitary arguments in additive combinatorics. The proof of Theorem 1 that I give below the fold is my attempt to achieve this, although to avoid a complete explosion of “epsilon management” I will still use at one juncture an ergodic theory reduction from the original paper of Kra et al. that relies on such infinitary tools as the ergodic decomposition, the ergodic theory, and the spectral theorem. Also some of the steps will be a little sketchy, and assume some familiarity with additive combinatorics tools (such as the arithmetic regularity lemma).

Marton’s conjecture in abelian groups with bounded torsion

Tim Gowers, Ben Green, Freddie Manners, and I have just uploaded to the arXiv our paper “Marton’s conjecture in abelian groups with bounded torsion“. This paper fully resolves a conjecture of Katalin Marton (the bounded torsion case of the Polynomial Freiman–Ruzsa conjecture (first proposed by Katalin Marton):

Theorem 1 (Marton’s conjecture) Let be an abelian -torsion group (thus, for all ), and let be such that . Then can be covered by at most translates of a subgroup of of cardinality at most . Moreover, is contained in for some .

We had previously established the case of this result, with the number of translates bounded by (which was subsequently improved to by Jyun-Jie Liao), but without the additional containment . It remains a challenge to replace by a bounded constant (such as ); this is essentially the “polynomial Bogolyubov conjecture”, which is still open. The result has been formalized in the proof assistant language Lean, as discussed in this previous blog post. As a consequence of this result, many of the applications of the previous theorem may now be extended from characteristic to higher characteristic.
Our proof techniques are a modification of those in our previous paper, and in particular continue to be based on the theory of Shannon entropy. For inductive purposes, it turns out to be convenient to work with the following version of the conjecture (which, up to -dependent constants, is actually equivalent to the above theorem):

Theorem 2 (Marton’s conjecture, entropy form) Let be an abelian -torsion group, and let be independent finitely supported random variables on , such that

where denotes Shannon entropy. Then there is a uniform random variable on a subgroup of such that

where denotes the entropic Ruzsa distance (see previous blog post for a definition); furthermore, if all the take values in some symmetric set , then lies in for some .

As a first approximation, one should think of all the as identically distributed, and having the uniform distribution on , as this is the case that is actually relevant for implying Theorem 1; however, the recursive nature of the proof of Theorem 2 requires one to manipulate the separately. It also is technically convenient to work with independent variables, rather than just a pair of variables as we did in the case; this is perhaps the biggest additional technical complication needed to handle higher characteristics.
The strategy, as with the previous paper, is to attempt an entropy decrement argument: to try to locate modifications of that are reasonably close (in Ruzsa distance) to the original random variables, while decrementing the “multidistance”

which turns out to be a convenient metric for progress (for instance, this quantity is non-negative, and vanishes if and only if the are all translates of a uniform random variable on a subgroup ). In the previous paper we modified the corresponding functional to minimize by some additional terms in order to improve the exponent , but as we are not attempting to completely optimize the constants, we did not do so in the current paper (and as such, our arguments here give a slightly different way of establishing the case, albeit with somewhat worse exponents).
As before, we search for such improved random variables by introducing more independent random variables – we end up taking an array of random variables for , with each a copy of , and forming various sums of these variables and conditioning them against other sums. Thanks to the magic of Shannon entropy inequalities, it turns out that it is guaranteed that at least one of these modifications will decrease the multidistance, except in an “endgame” situation in which certain random variables are nearly (conditionally) independent of each other, in the sense that certain conditional mutual informations are small. In particular, in the endgame scenario, the row sums of our array will end up being close to independent of the column sums , subject to conditioning on the total sum . Not coincidentally, this type of conditional independence phenomenon also shows up when considering row and column sums of iid independent gaussian random variables, as a specific feature of the gaussian distribution. It is related to the more familiar observation that if are two independent copies of a Gaussian random variable, then and are also independent of each other.
Up until now, the argument does not use the -torsion hypothesis, nor the fact that we work with an array of random variables as opposed to some other shape of array. But now the torsion enters in a key role, via the obvious identity

In the endgame, the any pair of these three random variables are close to independent (after conditioning on the total sum ). Applying some “entropic Ruzsa calculus” (and in particular an entropic version of the Balog–Szeméredi–Gowers inequality), one can then arrive at a new random variable of small entropic doubling that is reasonably close to all of the in Ruzsa distance, which provides the final way to reduce the multidistance.
Besides the polynomial Bogolyubov conjecture mentioned above (which we do not know how to address by entropy methods), the other natural question is to try to develop a characteristic zero version of this theory in order to establish the polynomial Freiman–Ruzsa conjecture over torsion-free groups, which in our language asserts (roughly speaking) that random variables of small entropic doubling are close (in Ruzsa distance) to a discrete Gaussian random variable, with good bounds. The above machinery is consistent with this conjecture, in that it produces lots of independent variables related to the original variable, various linear combinations of which obey the same sort of entropy estimates that gaussian random variables would exhibit, but what we are missing is a way to get back from these entropy estimates to an assertion that the random variables really are close to Gaussian in some sense. In continuous settings, Gaussians are known to extremize the entropy for a given variance, and of course we have the central limit theorem that shows that averages of random variables typically converge to a Gaussian, but it is not clear how to adapt these phenomena to the discrete Gaussian setting (without the circular reasoning of assuming the polynoimal Freiman–Ruzsa conjecture to begin with).

Talks at the JMM

Earlier this year, I gave a series of lectures at the Joint Mathematics Meetings at San Francisco. I am uploading here the slides for these talks:

• “Machine assisted proof” (Video here)
• “Translational tilings of Euclidean space” (Video here)
• “Correlations of multiplicative functions” (Video here)

I also have written a text version of the first talk, which has been submitted to the Notices of the American Mathematical Society.

Formalizing the proof of PFR in Lean4 using Blueprint: a short tour

Since the release of my preprint with Tim, Ben, and Freddie proving the Polynomial Freiman-Ruzsa (PFR) conjecture over , I (together with Yael Dillies and Bhavik Mehta) have started a collaborative project to formalize this argument in the proof assistant language Lean4. It has been less than a week since the project was launched, but it is proceeding quite well, with a significant fraction of the paper already either fully or partially formalized. The project has been greatly assisted by the Blueprint tool of Patrick Massot, which allows one to write a human-readable “blueprint” of the proof that is linked to the Lean formalization; similar blueprints have been used for other projects, such as Scholze’s liquid tensor experiment. For the PFR project, the blueprint can be found here. One feature of the blueprint that I find particularly appealing is the dependency graph that is automatically generated from the blueprint, and can provide a rough snapshot of how far along the formalization has advanced. For PFR, the latest state of the dependency graph can be found here. At the current time of writing, the graph looks like this:

The color coding of the various bubbles (for lemmas) and rectangles (for definitions) is explained in the legend to the dependency graph, but roughly speaking the green bubbles/rectangles represent lemmas or definitions that have been fully formalized, and the blue ones represent lemmas or definitions which are ready to be formalized (their statements, but not proofs, have already been formalized, as well as those of all prerequisite lemmas and proofs). The goal is to get all the bubbles leading up to and including the “pfr” bubble at the bottom colored in green.

In this post I would like to give a quick “tour” of the project, to give a sense of how it operates. If one clicks on the “pfr” bubble at the bottom of the dependency graph, we get the following:

Here, Blueprint is displaying a human-readable form of the PFR statement. This is coming from the corresponding portion of the blueprint, which also comes with a human-readable proof of this statement that relies on other statements in the project:

(I have cropped out the second half of the proof here, as it is not relevant to the discussion.)

Observe that the “pfr” bubble is white, but has a green border. This means that the statement of PFR has been formalized in Lean, but not the proof; and the proof itself is not ready to be formalized, because some of the prerequisites (in particular, “entropy-pfr” (Theorem 6.16)) do not even have their statements formalized yet. If we click on the “Lean” link below the description of PFR in the dependency graph, we are lead to the (auto-generated) Lean documentation for this assertion:

This is what a typical theorem in Lean looks like (after a procedure known as “pretty printing”). There are a number of hypotheses stated before the colon, for instance that is a finite elementary abelian group of order (this is how we have chosen to formalize the finite field vector spaces ), that is a non-empty subset of (the hypothesis that is non-empty was not stated in the LaTeX version of the conjecture, but we realized it was necessary in the formalization, and will update the LaTeX blueprint shortly to reflect this) with the cardinality of less than times the cardinality of , and the statement after the colon is the conclusion: that can be contained in the sum of a subgroup of and a set of cardinality at most .

The astute reader may notice that the above theorem seems to be missing one or two details, for instance it does not explicitly assert that is a subgroup. This is because the “pretty printing” suppresses some of the information in the actual statement of the theorem, which can be seen by clicking on the “Source” link:

Here we see that is required to have the “type” of an additive subgroup of . (Lean’s language revolves very strongly around types, but for this tour we will not go into detail into what a type is exactly.) The prominent “sorry” at the bottom of this theorem asserts that a proof is not yet provided for this theorem, but the intention of course is to replace this “sorry” with an actual proof eventually.

Filling in this “sorry” is too hard to do right now, so let’s look for a simpler task to accomplish instead. Here is a simple intermediate lemma “ruzsa-nonneg” that shows up in the proof:

The expression refers to something called the entropic Ruzsa distance between and , which is something that is defined elsewhere in the project, but for the current discussion it is not important to know its precise definition, other than that it is a real number. The bubble is blue with a green border, which means that the statement has been formalized, and the proof is ready to be formalized also. The blueprint dependency graph indicates that this lemma can be deduced from just one preceding lemma, called “ruzsa-diff“:

“ruzsa-diff” is also blue and bordered in green, so it has the same current status as “ruzsa-nonneg“: the statement is formalized, and the proof is ready to be formalized also, but the proof has not been written in Lean yet. The quantity , by the way, refers to the Shannon entropy of , defined elsewhere in the project, but for this discussion we do not need to know its definition, other than to know that it is a real number.

Looking at Lemma 3.11 and Lemma 3.13 it is clear how the former will imply the latter: the quantity is clearly non-negative! (There is a factor of present in Lemma 3.11, but it can be easily canceled out.) So it should be an easy task to fill in the proof of Lemma 3.13 assuming Lemma 3.11, even if we still don’t know how to prove Lemma 3.11 yet. Let’s first look at the Lean code for each lemma. Lemma 3.11 is formalized as follows:

Again we have a “sorry” to indicate that this lemma does not currently have a proof. The Lean notation (as well as the name of the lemma) differs a little from the LaTeX version for technical reasons that we will not go into here. (Also, the variables are introduced at an earlier stage in the Lean file; again, we will ignore this point for the ensuing discussion.) Meanwhile, Lemma 3.13 is currently formalized as

OK, I’m now going to try to fill in the latter “sorry”. In my local copy of the PFR github repository, I open up the relevant Lean file in my editor (Visual Studio Code, with the lean4 extension) and navigate to the “sorry” of “rdist_nonneg”. The accompanying “Lean infoview” then shows the current state of the Lean proof:

Here we see a number of ambient hypotheses (e.g., that is an additive commutative group, that is a map from to , and so forth; many of these hypotheses are not actually relevant for this particular lemma), and at the bottom we see the goal we wish to prove.

OK, so now I’ll try to prove the claim. This is accomplished by applying a series of “tactics” to transform the goal and/or hypotheses. The first step I’ll do is to put in the factor of that is needed to apply Lemma 3.11. This I will do with the “suffices” tactic, writing in the proof

I now have two goals (and two “sorries”): one to show that implies , and the other to show that . (The yellow squiggly underline indicates that this lemma has not been fully proven yet due to the presence of “sorry”s. The dot “.” is a syntactic marker that is useful to separate the two goals from each other, but you can ignore it for this tour.) The Lean tactic “suffices” corresponds, roughly speaking, to the phrase “It suffices to show that …” (or more precisely, “It suffices to show that … . To see this, … . It remains to verify the claim …”) in Mathematical English. For my own education, I wrote a “Lean phrasebook” of further correspondences between lines of Lean code and sentences or phrases in Mathematical English, which can be found here.

Let’s fill in the first “sorry”. The tactic state now looks like this (cropping out some irrelevant hypotheses):

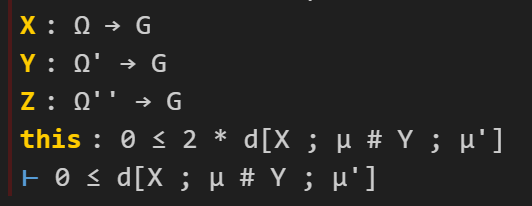
Here I can use a handy tactic “linarith“, which solves any goal that can be derived by linear arithmetic from existing hypotheses:

This works, and now the tactic state reports no goals left to prove on this branch, so we move on to the remaining sorry, in which the goal is now to prove :

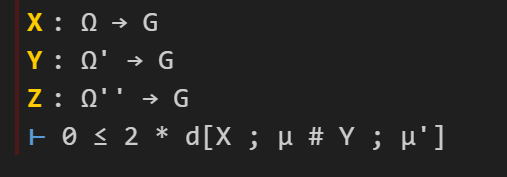
Here we will try to invoke Lemma 3.11. I add the following lines of code:

The Lean tactic “have” roughly corresponds to the Mathematical English phrase “We have the statement…” or “We claim the statement…”; like “suffices”, it splits a goal into two subgoals, though in the reversed order to “suffices”.

I again have two subgoals, one to prove the bound (which I will call “h”), and then to deduce the previous goal from . For the first, I know I should invoke the lemma “diff_ent_le_rdist” that is encoding Lemma 3.11. One way to do this is to try the tactic “exact?”, which will automatically search to see if the goal can already be deduced immediately from an existing lemma. It reports:

So I try this (by clicking on the suggested code, which automatically pastes it into the right location), and it works, leaving me with the final “sorry”:

The lean tactic “exact” corresponds, roughly speaking, to the Mathematical English phrase “But this is exactly …”.

At this point I should mention that I also have the Github Copilot extension to Visual Studio Code installed. This is an AI which acts as an advanced autocomplete that can suggest possible lines of code as one types. In this case, it offered a suggestion which was almost correct (the second line is what we need, whereas the first is not necessary, and in fact does not even compile in Lean):

In any event, “exact?” worked in this case, so I can ignore the suggestion of Copilot this time (it has been very useful in other cases though). I apply the “exact?” tactic a second time and follow its suggestion to establish the matching bound :

(One can find documention for the “abs_nonneg” method here. Copilot, by the way, was also able to resolve this step, albeit with a slightly different syntax; there are also several other search engines available to locate this method as well, such as Moogle. One of the main purposes of the Lean naming conventions for lemmas, by the way, is to facilitate the location of methods such as “abs_nonneg”, which is easier figure out how to search for than a method named (say) “Lemma 1.2.1”.) To fill in the final “sorry”, I try “exact?” one last time, to figure out how to combine and to give the desired goal, and it works!

Note that all the squiggly underlines have disappeared, indicating that Lean has accepted this as a valid proof. The documentation for “ge_trans” may be found here. The reader may observe that this method uses the relation rather than the relation, but in Lean the assertions and are “definitionally equal“, allowing tactics such as “exact” to use them interchangeably. “exact le_trans h’ h” would also have worked in this instance.

It is possible to compactify this proof quite a bit by cutting out several intermediate steps (a procedure sometimes known as “code golf“):

And now the proof is done! In the end, it was literally a “one-line proof”, which makes sense given how close Lemma 3.11 and Lemma 3.13 were to each other.

The current version of Blueprint does not automatically verify the proof (even though it does compile in Lean), so we have to manually update the blueprint as well. The LaTeX for Lemma 3.13 currently looks like this:

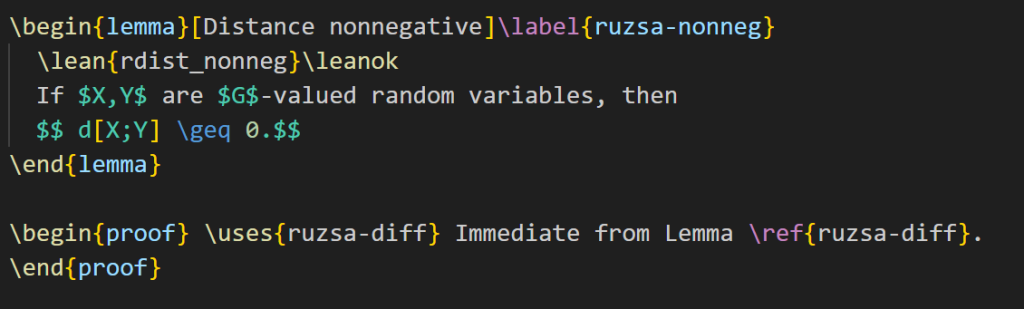
I add the “\leanok” macro to the proof, to flag that the proof has now been formalized:

I then push everything back up to the master Github repository. The blueprint will take quite some time (about half an hour) to rebuild, but eventually it does, and the dependency graph (which Blueprint has for some reason decided to rearrange a bit) now shows “ruzsa-nonneg” in green:

And so the formalization of PFR moves a little bit closer to completion. (Of course, this was a particularly easy lemma to formalize, that I chose to illustrate the process; one can imagine that most other lemmas will take a bit more work.) Note that while “ruzsa-nonneg” is now colored in green, we don’t yet have a full proof of this result, because the lemma “ruzsa-diff” that it relies on is not green. Nevertheless, the proof is locally complete at this point; hopefully at some point in the future, the predecessor results will also be locally proven, at which point this result will be completely proven. Note how this blueprint structure allows one to work on different parts of the proof asynchronously; it is not necessary to wait for earlier stages of the argument to be fully formalized to start working on later stages, although I anticipate a small amount of interaction between different components as we iron out any bugs or slight inaccuracies in the blueprint. (For instance, I am suspecting that we may need to add some measurability hypotheses on the random variables in the above two lemmas to make them completely true, but this is something that should emerge organically as the formalization process continues.)

That concludes the brief tour! If you are interested in learning more about the project, you can follow the Zulip chat stream; you can also download Lean and work on the PFR project yourself, using a local copy of the Github repository and sending pull requests to the master copy if you have managed to fill in one or more of the “sorry”s in the current version (but if you plan to work on anything more large scale than filling in a small lemma, it is good to announce your intention on the Zulip chat to avoid duplication of effort) . (One key advantage of working with a project based around a proof assistant language such as Lean is that it makes large-scale mathematical collaboration possible without necessarily having a pre-established level of trust amongst the collaborators; my fellow repository maintainers and I have already approved several pull requests from contributors that had not previously met, as the code was verified to be correct and we could see that it advanced the project. Conversely, as the above example should hopefully demonstrate, it is possible for a contributor to work on one small corner of the project without necessarily needing to understand all the mathematics that goes into the project as a whole.)

If one just wants to experiment with Lean without going to the effort of downloading it, you can playing try the “Natural Number Game” for a gentle introduction to the language, or the Lean4 playground for an online Lean server. Further resources to learn Lean4 may be found here.

On a conjecture of Marton

Tim Gowers, Ben Green, Freddie Manners, and I have just uploaded to the arXiv our paper “On a conjecture of Marton“. This paper establishes a version of the notorious Polynomial Freiman–Ruzsa conjecture (first proposed by Katalin Marton):

Theorem 1 (Polynomial Freiman–Ruzsa conjecture) Let be such that . Then can be covered by at most translates of a subspace of of cardinality at most .

The previous best known result towards this conjecture was by Konyagin (as communicated in this paper of Sanders), who obtained a similar result but with replaced by for any (assuming that say to avoid some degeneracies as approaches , which is not the difficult case of the conjecture). The conjecture (with replaced by an unspecified constant ) has a number of equivalent forms; see this survey of Green, and these papers of Lovett and of Green and myself for some examples; in particular, as discussed in the latter two references, the constants in the inverse theorem are now polynomial in nature (although we did not try to optimize the constant).

The exponent here was the product of a large number of optimizations to the argument (our original exponent here was closer to ), but can be improved even further with additional effort (our current argument, for instance, allows one to replace it with , but we decided to state our result using integer exponents instead).

In this paper we will focus exclusively on the characteristic case (so we will be cavalier in identifying addition and subtraction), but in a followup paper we will establish similar results in other finite characteristics.

Much of the prior progress on this sort of result has proceeded via Fourier analysis. Perhaps surprisingly, our approach uses no Fourier analysis whatsoever, being conducted instead entirely in “physical space”. Broadly speaking, it follows a natural strategy, which is to induct on the doubling constant . Indeed, suppose for instance that one could show that every set of doubling constant was “commensurate” in some sense to a set of doubling constant at most . One measure of commensurability, for instance, might be the Ruzsa distance , which one might hope to control by . Then one could iterate this procedure until doubling constant dropped below say , at which point the conjecture is known to hold (there is an elementary argument that if has doubling constant less than , then is in fact a subspace of ). One can then use several applications of the Ruzsa triangle inequality

to conclude (the fact that we reduce to means that the various Ruzsa distances that need to be summed are controlled by a convergent geometric series).

There are a number of possible ways to try to “improve” a set of not too large doubling by replacing it with a commensurate set of better doubling. We note two particular potential improvements:

• (i) Replacing with . For instance, if was a random subset (of density ) of a large subspace of , then replacing with usually drops the doubling constant from down to nearly (under reasonable choices of parameters).
• (ii) Replacing with for a “typical” . For instance, if was the union of random cosets of a subspace of large codimension, then replacing with again usually drops the doubling constant from down to nearly .

Unfortunately, there are sets where neither of the above two operations (i), (ii) significantly improves the doubling constant. For instance, if is a random density subset of random translates of a medium-sized subspace , one can check that the doubling constant stays close to if one applies either operation (i) or operation (ii). But in this case these operations don’t actually worsen the doubling constant much either, and by applying some combination of (i) and (ii) (either intersecting with a translate, or taking a sumset of with itself) one can start lowering the doubling constant again.

This begins to suggest a potential strategy: show that at least one of the operations (i) or (ii) will improve the doubling constant, or at least not worsen it too much; and in the latter case, perform some more complicated operation to locate the desired doubling constant improvement.

A sign that this strategy might have a chance of working is provided by the following heuristic argument. If has doubling constant , then the Cartesian product has doubling constant . On the other hand, by using the projection map defined by , we see that projects to , with fibres being essentially a copy of . So, morally, also behaves like a “skew product” of and the fibres , which suggests (non-rigorously) that the doubling constant of is also something like the doubling constant of , times the doubling constant of a typical fibre . This would imply that at least one of and would have doubling constant at most , and thus that at least one of operations (i), (ii) would not worsen the doubling constant.

Unfortunately, this argument does not seem to be easily made rigorous using the traditional doubling constant; even the significantly weaker statement that has doubling constant at most is false (see comments for more discussion). However, it turns out (as discussed in this recent paper of myself with Green and Manners) that things are much better. Here, the analogue of a subset in is a random variable taking values in , and the analogue of the (logarithmic) doubling constant is the entropic doubling constant , where are independent copies of . If is a random variable in some additive group and is a homomorphism, one then has what we call the fibring inequality

where the conditional doubling constant is defined as

Indeed, from the chain rule for Shannon entropy one has

and

while from the non-negativity of conditional mutual information one has

and it is an easy matter to combine all these identities and inequalities to obtain the claim.

Applying this inequality with replaced by two independent copies of itself, and using the addition map for , we obtain in particular that

or (since is determined by once one fixes )

So if , then at least one of or will be less than or equal to . This is the entropy analogue of at least one of (i) or (ii) improving, or at least not degrading the doubling constant, although there are some minor technicalities involving how one deals with the conditioning to in the second term that we will gloss over here (one can pigeonhole the instances of to different events , , and “depolarise” the induction hypothesis to deal with distances between pairs of random variables that do not necessarily have the same distribution). Furthermore, we can even calculate the defect in the above inequality: a careful inspection of the above argument eventually reveals that

where we now take four independent copies . This leads (modulo some technicalities) to the following interesting conclusion: if neither (i) nor (ii) leads to an improvement in the entropic doubling constant, then and are conditionally independent relative to . This situation (or an approximation to this situation) is what we refer to in the paper as the “endgame”.

A version of this endgame conclusion is in fact valid in any characteristic. But in characteristic , we can take advantage of the identity

Conditioning on , and using symmetry we now conclude that if we are in the endgame exactly (so that the mutual information is zero), then the independent sum of two copies of has exactly the same distribution; in particular, the entropic doubling constant here is zero, which is certainly a reduction in the doubling constant.

To deal with the situation where the conditional mutual information is small but not completely zero, we have to use an entropic version of the Balog-Szemeredi-Gowers lemma, but fortunately this was already worked out in an old paper of mine (although in order to optimise the final constant, we ended up using a slight variant of that lemma).

I am planning to formalize this paper in the Lean4 language. Further discussion of this project will take place on this Zulip stream, and the project itself will be held at this Github repository.

Undecidability of translational monotilings

Rachel Greenfeld and I have just uploaded to the arXiv our paper “Undecidability of translational monotilings“. This is a sequel to our previous paper in which we constructed a translational monotiling of a high-dimensional lattice (thus the monotile is a finite set and the translates , of partition ) which was aperiodic (there is no way to “repair” this tiling into a periodic tiling , in which is now periodic with respect to a finite index subgroup of ). This disproved the periodic tiling conjecture of Stein, Grunbaum-Shephard and Lagarias-Wang, which asserted that such aperiodic translational monotilings do not exist. (Compare with the “hat monotile“, which is a recently discovered aperiodic isometric monotile for of , where one is now allowed to use rotations and reflections as well as translations, or the even more recent “spectre monotile“, which is similar except that no reflections are needed.)

One of the motivations of this conjecture was the observation of Hao Wang that if the periodic tiling conjecture were true, then the translational monotiling problem is (algorithmically) decidable: there is a Turing machine which, when given a dimension and a finite subset of , can determine in finite time whether can tile . This is because if a periodic tiling exists, it can be found by computer search; and if no tiling exists at all, then (by the compactness theorem) there exists some finite subset of that cannot be covered by disjoint translates of , and this can also be discovered by computer search. The periodic tiling conjecture asserts that these are the only two possible scenarios, thus giving the decidability.

On the other hand, Wang’s argument is not known to be reversible: the failure of the periodic tiling conjecture does not automatically imply the undecidability of the translational monotiling problem, as it does not rule out the existence of some other algorithm to determine tiling that does not rely on the existence of a periodic tiling. (For instance, even with the newly discovered hat and spectre tiles, it remains an open question whether the isometric monotiling problem for (say) polygons with rational coefficients in is decidable, with or without reflections.)

The main result of this paper settles this question (with one caveat):

Theorem 1 There does not exist any algorithm which, given a dimension , a periodic subset of , and a finite subset of , determines in finite time whether there is a translational tiling of by .

The caveat is that we have to work with periodic subsets of , rather than all of ; we believe this is largely a technical restriction of our method, and it is likely that can be removed with additional effort and creativity. We also remark that when , the periodic tiling conjecture was established by Bhattacharya, and so the problem is decidable in the case. It remains open whether the tiling problem is decidable for any fixed value of (note in the above result that the dimension is not fixed, but is part of the input).

Because of a well known link between algorithmic undecidability and logical undecidability (also known as logical independence), the main theorem also implies the existence of an (in principle explicitly describable) dimension , periodic subset of , and a finite subset of , such that the assertion that tiles by translation cannot be proven or disproven in ZFC set theory (assuming of course that this theory is consistent).

As a consequence of our method, we can also replace here by “virtually two-dimensional” groups , with a finite abelian group (which now becomes part of the input, in place of the dimension ).

We now describe some of the main ideas of the proof. It is a common technique to show that a given problem is undecidable by demonstrating that some other problem that was already known to be undecidable can be “encoded” within the original problem, so that any algorithm for deciding the original problem would also decide the embedded problem. Accordingly, we will encode the Wang tiling problem as a monotiling problem in :

Problem 2 (Wang tiling problem) Given a finite collection of Wang tiles (unit squares with each side assigned some color from a finite palette), is it possible to tile the plane with translates of these tiles along the standard lattice , such that adjacent tiles have matching colors along their common edge?

It is a famous result of Berger that this problem is undecidable. The embedding of this problem into the higher-dimensional translational monotiling problem proceeds through some intermediate problems. Firstly, it is an easy matter to embed the Wang tiling problem into a similar problem which we call the domino problem:

Problem 3 (Domino problem) Given a finite collection (resp. ) of horizontal (resp. vertical) dominoes – pairs of adjacent unit squares, each of which is decorated with an element of a finite set of “pips”, is it possible to assign a pip to each unit square in the standard lattice tiling of , such that every horizontal (resp. vertical) pair of squares in this tiling is decorated using a domino from (resp. )?

Indeed, one just has to interpet each Wang tile as a separate “pip”, and define the domino sets , to be the pairs of horizontally or vertically adjacent Wang tiles with matching colors along their edge.

Next, we embed the domino problem into a Sudoku problem:

Problem 4 (Sudoku problem) Given a column width , a digit set , a collection of functions , and an “initial condition” (which we will not detail here, as it is a little technical), is it possible to assign a digit to each cell in the “Sudoku board” such that for any slope and intercept , the digits along the line lie in (and also that obeys the initial condition )?

The most novel part of the paper is the demonstration that the domino problem can indeed be embedded into the Sudoku problem. The embedding of the Sudoku problem into the monotiling problem follows from a modification of the methods in our previous papers, which had also introduced versions of the Sudoku problem, and created a “tiling language” which could be used to “program” various problems, including the Sudoku problem, as monotiling problems.

To encode the domino problem into the Sudoku problem, we need to take a domino function (obeying the domino constraints associated to some domino sets ) and use it to build a Sudoku function (obeying some Sudoku constraints relating to the domino sets); conversely, every Sudoku function obeying the rules of our Sudoku puzzle has to arise somehow from a domino function. The route to doing so was not immediately obvious, but after a helpful tip from Emmanuel Jeandel, we were able to adapt some ideas of Aanderaa and Lewis, in which certain hierarchical structures were used to encode one problem in another. Here, we interpret hierarchical structure -adically (using two different primes due to the two-dimensionality of the domino problem). The Sudoku function that will exemplify our embedding is then built from by the formula

where are two large distinct primes (for instance one can take , for concreteness), denotes the number of times divides , and is the last non-zero digit in the base expansion of :

(with the conventions and ). In the case , the first component of (1) looks like this:

and a typical instance of the final component looks like this:

Amusingly, the decoration here is essentially following the rules of the children’s game “Fizz buzz“.

To demonstrate the embedding, we thus need to produce a specific Sudoku rule (as well as a more technical initial condition , which is basically required to exclude degenerate Sudoku solutions such as a constant solution) that can “capture” the target function (1), in the sense that the only solutions to this specific Sudoku puzzle are given by variants of (e.g., composed with various linear transformations). In our previous paper we were able to build a Sudoku puzzle that could similarly capture either of the first two components , of our target function (1) (up to linear transformations), by a procedure very akin to solving an actual Sudoku puzzle (combined with iterative use of a “Tetris” move in which we eliminate rows of the puzzle that we have fully solved, to focus on the remaining unsolved rows). Our previous paper treated the case when was replaced with a power of , as this was the only case that we know how to embed in a monotiling problem of the entirety of (as opposed to a periodic subset of ), but the analysis is in fact easier when is a large odd prime, instead of a power of . Once the first two components have been solved for, it is a relatively routine matter to design an additional constraint in the Sudoku rule that then constrains the third component to be of the desired form , with obeying the domino constraints.

Sumsets and entropy revisited

Ben Green, Freddie Manners and I have just uploaded to the arXiv our preprint “Sumsets and entropy revisited“. This paper uses entropy methods to attack the Polynomial Freiman-Ruzsa (PFR) conjecture, which we study in the following two forms:

Conjecture 1 (Weak PFR over ) Let be a finite non-empty set whose doubling constant is at most . Then there is a subset of of density that has affine dimension (i.e., it is contained in an affine space of dimension ).

Conjecture 2 (PFR over ) Let be a non-empty set whose doubling constant is at most . Then can be covered by cosets of a subspace of cardinality at most .

Our main results are then as follows.

Theorem 3 If with , then

• (i) There is a subset of of density of “skew-dimension” (or “query complexity”) .
• (ii) There is a subset of of density of affine dimension (where goes to zero as ).
• (iii) If Conjecture 2 holds, then there is a subset of of density of affine dimension . In other words, Conjecture 2 implies Conjecture 1.

The skew-dimension of a set is a quantity smaller than the affine dimension which is defined recursively; the precise definition is given in the paper, but suffice to say that singleton sets have dimension , and a set whose projection to has skew-dimension at most , and whose fibers in have skew-dimension at most for any , will have skew-dimension at most . (In fact, the skew-dimension is basically the largest quantity which obeys all of these properties.)

Part (i) of this theorem was implicitly proven by Pálvölgi and Zhelezov by a different method. Part (ii) with replaced by was established by Manners. To our knowledge, part (iii) is completely new.

Our proof strategy is to establish these combinatorial additive combinatorics results by using entropic additive combinatorics, in which we replace sets with random variables , and cardinality with (the exponential of) Shannon entropy. This is in order to take advantage of some superior features of entropic additive combinatorics, most notably good behavior with respect to homomorphisms.

For instance, the analogue of the combinatorial doubling constant of a finite non-empty subset of an abelian group , is the entropy doubling constant

of a finitely-valued random variable in , where are independent copies of and denotes Shannon entropy. There is also an analogue of the Ruzsa distance

between two finite non-empty subsets of , namely the entropic Ruzsa distance

where are independent copies of respectively. (Actually, one thing we show in our paper is that the independence hypothesis can be dropped, and this only affects the entropic Ruzsa distance by a factor of three at worst.) Many of the results about sumsets and Ruzsa distance have entropic analogues, but the entropic versions are slightly better behaved; for instance, we have a contraction property

whenever is a homomorphism. In fact we have a refinement of this inequality in which the gap between these two quantities can be used to control the entropic distance between “fibers” of (in which one conditions and to be fixed). On the other hand, there are direct connections between the combinatorial and entropic sumset quantities. For instance, if is a random variable drawn uniformly from , then

Thus if has small doubling, then has small entropic doubling. In the converse direction, if has small entropic doubling, then is close (in entropic Ruzsa distance) to a uniform random variable drawn from a set of small doubling; a version of this statement was proven in an old paper of myself, but we establish here a quantitatively efficient version, established by rewriting the entropic Ruzsa distance in terms of certain Kullback-Liebler divergences.

Our first main result is a “99% inverse theorem” for entropic Ruzsa distance: if is sufficiently small, then there exists a finite subgroup of such that

This result uses the results just mentioned to relate to a set of small doubling, which can then be related to a subgroup by standard inverse theorems; this gives a weak version of (1) (roughly speaking losing a square root in the bound), and some additional analysis is needed to bootstrap this initial estimate back to (1).

We now sketch how these tools are used to prove our main theorem. For (i), we reduce matters to establishing the following bilinear entropic analogue: given two non-empty finite subsets of , one can find subsets , with

such that have skew-dimension at most , for some absolute constant . This can be shown by an induction on (say). One applies a non-trivial coordinate projection to . If and are very close in entropic Ruzsa distance, then the 99% inverse theorem shows that these random variables must each concentrate at a point (because has no non-trivial finite subgroups), and can pass to a fiber of these points and use the induction hypothesis. If instead and are far apart, then by the behavior of entropy under projections one can show that the fibers of and under are closer on average in entropic Ruzsa distance of and themselves, and one can again proceed using the induction hypothesis.

For parts (ii) and (iii), we first use an entropic version of an observation of Manners that sets of small doubling in must be irregularly distributed modulo . A clean formulation of this in entropic language is the inequality

whenever take values in a torsion-free abelian group such as ; this turns out to follow from two applications of the entropy submodularity inequality. One corollary of this (and the behavior of entropy under projections) is that

This is the key link between the and worlds that is used to prove (ii), (iii): while (iii) relies on the still unproven PFR conjecture over , (ii) uses the unconditional progress on PFR by Konyagin, as detailed in this survey of Sanders. The argument has a similar inductive structure to that used to establish (i) (and if one is willing to replace by then the argument is in fact relatively straightforward and does not need any deep partial results on the PFR).

As one byproduct of our analysis we also obtain an appealing entropic reformulation of Conjecture 2, namely that if is an -valued random variable then there exists a subspace of such that

Right now the best result in this direction is

for any , by using Konyagin’s partial result towards the PFR.

Sums of GUE matrices and concentration of hives from correlation decay of eigengaps

Hariharan Narayanan, Scott Sheffield, and I have just uploaded to the arXiv our paper “Sums of GUE matrices and concentration of hives from correlation decay of eigengaps“. This is a personally satisfying paper for me, as it connects the work I did as a graduate student (with Allen Knutson and Chris Woodward) on sums of Hermitian matrices, with more recent work I did (with Van Vu) on random matrix theory, as well as several other results by other authors scattered across various mathematical subfields.

Suppose are two Hermitian matrices with eigenvalues and respectively (arranged in non-increasing order. What can one say about the eigenvalues of the sum ? There are now many ways to answer this question precisely; one of them, introduced by Allen and myself many years ago, is that there exists a certain triangular array of numbers called a “hive” that has as its boundary values. On the other hand, by the pioneering work of Voiculescu in free probability, we know in the large limit that if are asymptotically drawn from some limiting distribution, and and are drawn independently at random (using the unitarily invariant Haar measure) amongst all Hermitian matrices with the indicated eigenvalues, then (under mild hypotheses on the distribution, and under suitable normalization), will almost surely have a limiting distribution that is the free convolution of the two original distributions.

One of my favourite open problems is to come up with a theory of “free hives” that allows one to explain the latter fact from the former. This is still unresolved, but we are now beginning to make a bit of progress towards this goal. We know (for instance from the calculations of Coquereaux and Zuber) that if are drawn independently at random with eigenvalues , then the eigenvalues of are distributed according to the boundary values of an “augmented hive” with two boundaries , drawn uniformly at random from the polytope of all such augmented hives. (This augmented hive is basically a regular hive with another type of pattern, namely a Gelfand-Tsetlin pattern, glued to one side of it.) So, if one could show some sort of concentration of measure for the entries of this augmented hive, and calculate what these entries concentrated to, one should presumably be able to recover Voiculescu’s result after some calculation.

In this paper, we are able to accomplish the first half of this goal, assuming that the spectra are not deterministic, but rather drawn from the spectra of rescaled GUE matrices (thus are independent rescaled copies of the GUE ensemble). We have chosen to normalize matters so that the eigenvalues have size , so that the entries of the augmented hive have entries . Our result is then that the entries of the augmented hive in fact have a standard deviation of , thus exhibiting a little bit of concentration. (Actually, from the Brunn-Minkowski inequality, the distribution of these entries is log concave, so once once controls the standard deviation one also gets a bit of exponential decay beyond the standard deviation; Narayanan and Sheffield had also recently established the existence of a rate function for this sort of model.) Presumably one should get much better concentration, and one should be able to handle other models than the GUE ensemble, but this is the first advance that we were able to achieve.

Augmented hives seem tricky to work with directly, but by adapting the octahedron recurrence introduced for this problem by Knutson, Woodward, and myself some time ago (which is related to the associativity of addition for Hermitian matrices), one can construct a piecewise linear volume-preserving map between the cone of augmented hives, and the product of two Gelfand-Tsetlin cones. The problem then reduces to establishing concentration of measure for certain piecewise linear maps on products of Gelfand-Tsetlin cones (endowed with a certain GUE-type measure). This is a promising formulation because Gelfand-Tsetlin cones are by now quite well understood.

On the other hand, the piecewise linear map, initially defined by iterating the octahedron relation , looks somewhat daunting. Fortunately, there is an explicit formulation of this map due to Speyer, as the supremum of certain linear maps associated to perfect matchings of a certain “excavation graph”. For us it was convenient to work with the dual of this excavation graph, and associate these linear maps to certain “lozenge tilings” of a hexagon.

It would be more convenient to study the concentration of each linear map separately, rather than their supremum. By the Cheeger inequality, it turns out that one can relate the latter to the former provided that one has good control on the Cheeger constant of the underlying measure on the Gelfand-Tsetlin cones. Fortunately, the measure is log-concave, so one can use the very recent work of Klartag on the KLS conjecture to eliminate the supremum (up to a logarithmic loss which is only moderately annoying to deal with).

It remains to obtain concentration on the linear map associated to a given lozenge tiling. After stripping away some contributions coming from lozenges near the edge (using some eigenvalue rigidity results of Van Vu and myself), one is left with some bulk contributions which ultimately involve eigenvalue interlacing gaps such as

where is the eigenvalue of the top left minor of , and is in the bulk region for some fixed . To get the desired result, one needs some non-trivial correlation decay in for these statistics. If one was working with eigenvalue gaps rather than interlacing results, then such correlation decay was conveniently obtained for us by recent work of Cippoloni, Erdös, and Schröder. So the last remaining challenge is to understand the relation between eigenvalue gaps and interlacing gaps.

For this we turned to the work of Metcalfe, who uncovered a determinantal process structure to this problem, with a kernel associated to Lagrange interpolation polynomials. It is possible to satisfactorily estimate various integrals of these kernels using the residue theorem and eigenvalue rigidity estimates, thus completing the required analysis.

A Host–Kra F^omega_2-system of order 5 that is not Abramov of order 5, and non-measurability of the inverse theorem for the U^6(F^n_2) norm; The structure of totally disconnected Host–Kra–Ziegler factors, and the inverse theorem for the U^k Gowers uniformity norms on finite abelian groups of bounded torsion

Asgar Jamneshan, Or Shalom, and myself have just uploaded to the arXiv our preprints “A Host–Kra -system of order 5 that is not Abramov of order 5, and non-measurability of the inverse theorem for the norm” and “The structure of totally disconnected Host–Kra–Ziegler factors, and the inverse theorem for the Gowers uniformity norms on finite abelian groups of bounded torsion“. These two papers are both concerned with advancing the inverse theory for the Gowers norms and Gowers-Host-Kra seminorms; the first paper provides a counterexample in this theory (in particular disproving a conjecture of Bergelson, Ziegler and myself), and the second paper gives new positive results in the case when the underlying group is bounded torsion, or the ergodic system is totally disconnected. I discuss the two papers more below the fold.