In the previous two quarters, we have been focusing largely on the “soft” side of real analysis, which is primarily concerned with “qualitative” properties such as convergence, compactness, measurability, and so forth. In contrast, we will begin this quarter with more of an emphasis on the “hard” side of real analysis, in which we study estimates and upper and lower bounds of various quantities, such as norms of functions or operators. (Of course, the two sides of analysis are closely connected to each other; an understanding of both sides and their interrelationships, are needed in order to get the broadest and most complete perspective for this subject.)
One basic tool in hard analysis is that of interpolation, which allows one to start with a hypothesis of two (or more) “upper bound” estimates, e.g. and
, and conclude a family of intermediate estimates
(or maybe
, where
is a constant) for any choice of parameter
. Of course, interpolation is not a magic wand; one needs various hypotheses (e.g. linearity, sublinearity, convexity, or complexifiability) on
in order for interpolation methods to be applicable. Nevertheless, these techniques are available for many important classes of problems, most notably that of establishing boundedness estimates such as
for linear (or “linear-like”) operators
from one Lebesgue space
to another
. (Interpolation can also be performed for many other normed vector spaces than the Lebesgue spaces, but we will just focus on Lebesgue spaces in these notes to focus the discussion.) Using interpolation, it is possible to reduce the task of proving such estimates to that of proving various “endpoint” versions of these estimates. In some cases, each endpoint only faces a portion of the difficulty that the interpolated estimate did, and so by using interpolation one has split the task of proving the original estimate into two or more simpler subtasks. In other cases, one of the endpoint estimates is very easy, and the other one is significantly more difficult than the original estimate; thus interpolation does not really simplify the task of proving estimates in this case, but at least clarifies the relative difficulty between various estimates in a given family.
As is the case with many other tools in analysis, interpolation is not captured by a single “interpolation theorem”; instead, there are a family of such theorems, which can be broadly divided into two major categories, reflecting the two basic methods that underlie the principle of interpolation. The real interpolation method is based on a divide and conquer strategy: to understand how to obtain control on some expression such as for some operator
and some function
, one would divide
into two or more components, e.g. into components where
is large and where
is small, or where
is oscillating with high frequency or only varying with low frequency. Each component would be estimated using a carefully chosen combination of the extreme estimates available; optimising over these choices and summing up (using whatever linearity-type properties on
are available), one would hope to get a good estimate on the original expression. The strengths of the real interpolation method are that the linearity hypotheses on
can be relaxed to weaker hypotheses, such as sublinearity or quasilinearity; also, the endpoint estimates are allowed to be of a weaker “type” than the interpolated estimates. On the other hand, the real interpolation often concedes a multiplicative constant in the final estimates obtained, and one is usually obligated to keep the operator
fixed throughout the interpolation process. The proofs of real interpolation theorems are also a little bit messy, though in many cases one can simply invoke a standard instance of such theorems (e.g. the Marcinkiewicz interpolation theorem) as a black box in applications.
The complex interpolation method instead proceeds by exploiting the powerful tools of complex analysis, in particular the maximum modulus principle and its relatives (such as the Phragmén-Lindelöf principle). The idea is to rewrite the estimate to be proven (e.g. ) in such a way that it can be embedded into a family of such estimates which depend holomorphically on a complex parameter
in some domain (e.g. the strip
. One then exploits things like the maximum modulus principle to bound an estimate corresponding to an interior point of this domain by the estimates on the boundary of this domain. The strengths of the complex interpolation method are that it typically gives cleaner constants than the real interpolation method, and also allows the underlying operator
to vary holomorphically with respect to the parameter
, which can significantly increase the flexibility of the interpolation technique. The proofs of these methods are also very short (if one takes the maximum modulus principle and its relatives as a black box), which make the method particularly amenable for generalisation to more intricate settings (e.g. multilinear operators, mixed Lebesgue norms, etc.). On the other hand, the somewhat rigid requirement of holomorphicity makes it much more difficult to apply this method to non-linear operators, such as sublinear or quasilinear operators; also, the interpolated estimate tends to be of the same “type” as the extreme ones, so that one does not enjoy the upgrading of weak type estimates to strong type estimates that the real interpolation method typically produces. Also, the complex method runs into some minor technical problems when target space
ceases to be a Banach space (i.e. when
) as this makes it more difficult to exploit duality.
Despite these differences, the real and complex methods tend to give broadly similar results in practice, especially if one is willing to ignore constant losses in the estimates or epsilon losses in the exponents.
The theory of both real and complex interpolation can be studied abstractly, in general normed or quasi-normed spaces; see e.g. this book for a detailed treatment. However in these notes we shall focus exclusively on interpolation for Lebesgue spaces (and their cousins, such as the weak Lebesgue spaces
and the Lorentz spaces
).
— 1. Interpolation of scalars —
As discussed in the introduction, most of the interesting applications of interpolation occur when the technique is applied to operators . However, in order to gain some intuition as to why interpolation works in the first place, let us first consider the significantly simpler (though rather trivial) case of interpolation in the case of scalars or functions.
We begin first with scalars. Suppose that are non-negative real numbers such that
indeed one simply raises (1) to the power , (2) to the power
, and multiplies the two inequalities together. Thus for instance, when
one obtains the geometric mean of (1) and (2):
One can view and
as the unique log-linear functions of
(i.e.
,
are (affine-)linear functions of
) which equal their boundary values
and
respectively as
.
Example 1 If
and
for some
and
, then the log-linear interpolant
is given by
, where
is the quantity such that
.
The deduction of (3) from (1), (2) is utterly trivial, but there are still some useful lessons to be drawn from it. For instance, let us take for simplicity, so we are interpolating two upper bounds
,
on the same quantity
to give a new bound
. But actually we have a refinement available to this bound, namely
for any sufficiently small (indeed one can take any
less than or equal to
). Indeed one sees this simply by applying (3) with
with
and
and taking minima. Thus we see that (3) is only sharp when the two original bounds
are comparable; if instead we have
for some integer
, then (6) tells us that we can improve (3) by an exponentially decaying factor of
. The geometric series formula tells us that such factors are absolutely summable, and so in practice it is often a useful heuristic to pretend that the
cases dominate so strongly that the other cases can be viewed as negligible by comparison.
Also, one can trivially extend the deduction of (3) from (1), (2) as follows: if is a function from
to
which is log-convex (thus
is a convex function of
, and (1), (2) hold for some
, then (3) holds for all intermediate
also, where
is of course defined by (5). Thus one can interpolate upper bounds on log-convex functions. However, one certainly cannot interpolate lower bounds: lower bounds on a log-convex function
at
and
yield no information about the value of, say,
. Similarly, one cannot extrapolate upper bounds on log-convex functions: an upper bound on, say,
and
does not give any information about
. (However, an upper bound on
coupled with a lower bound on
gives a lower bound on
; this is the contrapositive of an interpolation statement.)
Exercise 2 Show that the sum
, product
, or pointwise maximum
of two log-convex functions
is log-convex.
Remark 3 Every non-negative log-convex function
is convex, thus in particular
for all
(note that this generalises the arithmetic mean-geometric mean inequality). Of course, the converse statement is not true.
Now we turn to the complex version of the interpolation of log-convex functions, a result known as Lindelöf’s theorem:
Theorem 4 (Lindelöf’s theorem) Let
be a holomorphic function on the strip
, which obeys the bound
for all
and some constants
. Suppose also that
and
for all
. Then we have
for all
and
, where
is of course defined by (5).
Remark 5 The hypothesis (7) is a qualitative hypothesis rather than a quantitative one, since the exact values of
do not show up in the conclusion. It is quite a mild condition; any function of exponential growth in
, or even with such super-exponential growth as
or
, will obey (7). The principle however fails without this hypothesis, as one can see for instance by considering the holomorphic function
.
Proof: Observe that the function is holomorphic and non-zero on
, and has magnitude exactly
on the line
for each
. Thus, by dividing
by this function (which worsens the qualitative bound (7) slightly) we may reduce to the case when
for all
.
Suppose we temporarily assume that as
. Then by the maximum modulus principle (applied to a sufficiently large rectangular portion of the strip), it must then attain a maximum on one of the two sides of the strip. But
on these two sides, and so
on the interior as well.
To remove the assumption that goes to zero at infinity, we use the trick of giving ourselves an epsilon of room. Namely, we multiply
by the holomorphic function
for some
. A little complex arithmetic shows that the function
goes to zero at infinity in
(the
factor decays fast enough to damp out the growth of
as
, while the
damps out the growth as
), and is bounded in magnitude by
on both sides of the strip
. Applying the previous case to this function, then taking limits as
, we obtain the claim.
Exercise 6 With the notation and hypotheses of Theorem 4, show that the function
is log-convex on
.
Exercise 7 (Hadamard three-circles theorem) Let
be a holomorphic function on an annulus
. Show that the function
is log-convex on
.
Exercise 8 (Phragmén-Lindelöf principle) Let
be as in Theorem 4, but suppose that we have the bounds
and
for all
and some exponents
and a constant
. Show that one has
for all
and some constant
(which is allowed to depend on the constants
in (7)). (Hint: it is convenient to work first in a half-strip such as
for some large
. Then multiply
by something like
for some suitable branch of the logarithm and apply a variant of Theorem 4 for the half-strip. A more refined estimate in this regard is due to Rademacher.) This particular version of the principle gives the convexity bound for Dirichlet series such as the Riemann zeta function. Bounds which exploit the deeper properties of these functions to improve upon the convexity bound are known as subconvexity bounds and are of major importance in analytic number theory, which is of course well outside the scope of this course.
— 2. Interpolation of functions —
We now turn to the interpolation in function spaces, focusing particularly on the Lebesgue spaces and the weak Lebesgue spaces
. Here,
is a fixed measure space. It will not matter much whether we deal with real or complex spaces; for sake of concretness we work with complex spaces. Then for
, recall (see 245B Notes 3) that
is the space of all functions
whose
norm
is finite, modulo almost everywhere equivalence. The space is defined similarly, but where
is the essential supremum of
on
.
A simple test case in which to understand the norms better is that of a step function
, where
is a non-negative number and
a set of finite measure. Then one has
for
. Observe that this is a log-convex function of
. This is a general phenomenon:
Lemma 9 (Log-convexity of
norms) Let that
and
. Then
for all
, and furthermore we have
for all
, where the exponent
is defined by
.
In particular, we see that the function
is log-convex whenever the right-hand side is finite (and is in fact log-convex for all
, if one extends the definition of log-convexity to functions that can take the value
). In other words, we can interpolate any two bounds
and
to obtain
for all
.
Let us give several proofs of this lemma. We will focus on the case ; the endpoint case
can be proven directly, or by modifying the arguments below, or by using an appropriate limiting argument, and we leave the details to the reader.
The first proof is to use Hölder’s inequality
when is finite (with some minor modifications in the case
).
Another (closely related) proof proceeds by using the log-convexity inequality
for all , where
is the quantity such that
. If one integrates this inequality in
, one already obtains the claim in the normalised case when
. To obtain the general case, one can multiply the function
and the measure
by appropriately chosen constants to obtain the above normalisation; we leave the details as an exercise to the reader. (The case when
or
vanishes is of course easy to handle separately.)
A third approach is more in the spirit of the real interpolation method, avoiding the use of convexity arguments. As in the second proof, we can reduce to the normalised case . We then split
, where
is the indicator function to the set
, and similarly for
. Observe that
and similarly
and so by the quasi-triangle inequality (or triangle inequality, when )
for some constant depending on
. Note, by the way, that this argument gives the inclusions
This is off by a constant factor by what we want. But one can eliminate this constant by using the tensor power trick. Indeed, if one replaces with a Cartesian power
(with the product
-algebra
and product measure
), and replace
by the tensor power
, we see from many applications of the Fubini-Tonelli theorem that
for all . In particular,
obeys the same normalisation hypotheses as
, and thus by applying the previous inequality to
, we obtain
for every , where it is key to note that the constant
on the right is independent of
. Taking
roots and then sending
, we obtain the claim.
Finally, we give a fourth proof in the spirit of the complex interpolation method. By replacing by
we may assume
is non-negative. By expressing non-negative measurable functions as the monotone limit of simple functions and using the monotone convergence theorem, we may assume that
is a simple function, which is then necessarily of finite measure support from the
finiteness hypotheses. Now consider the function
. Expanding
out in terms of step functions we see that this is an analytic function of
which grows at most exponentially in
; also, by the triangle inequality this function has magnitude at most
when
and magnitude
when
. Applying Theorem 4 and specialising to the value of
for which
we obtain the claim.
Exercise 10 If
, show that equality holds in Lemma 9 if and only if
is a step function.
Now we consider variants of interpolation in which the “strong” spaces are replaced by their “weak” counterparts
. Given a measurable function
, we define the distribution function
by the formula
This distribution function is closely connected to the norms. Indeed, from the calculus identity
and the Fubini-Tonelli theorem, we obtain the formula
for all , thus the
norms are essentially moments of the distribution function. The
norm is of course related to the distribution function by the formula
Exercise 11 Show that we have the relationship
for any measurable
and
, where we use
to denote a pair of inequalities of the form
for some constants
depending only on
. (Hint:
is non-increasing in
.) Thus we can relate the
norms of
to the dyadic values
of the distribution function; indeed, for any
,
is comparable (up to constant factors depending on
) to the
norm of the sequence
.
Another relationship between the norms and the distribution function is given by observing that
for any , leading to Chebyshev’s inequality
(The version of this inequality is also known as Markov’s inequality. In probability theory, Chebyshev’s inequality is often specialised to the case
, and with
replaced by a normalised function
. Note that, as with many other Cyrillic names, there are also a large number of alternative spellings of Chebyshev in the Roman alphabet.)
Chebyshev’s inequality motivates one to define the weak norm
of a measurable function
for
by the formula
thus Chebyshev’s inequality can be expressed succinctly as
It is also natural to adopt the convention that . If
are two functions, we have the inclusion
and hence
this easily leads to the quasi-triangle inequality
where we use as shorthand for the inequality
for some constant
depending only on
(it can be a different constant at each use of the
notation). [Note: in analytic number theory, it is more customary to use
instead of
, following Vinogradov. However, in analysis
is sometimes used instead to denote “much smaller than”, e.g.
denotes the assertion
for some sufficiently small constant
.]
Let be the space of all
which have finite
, modulo almost everywhere equivalence; this space is also known as weak
. The quasi-triangle inequality soon implies that
is a quasi-normed vector space with the
quasi-norm, and Chebyshev’s inequality asserts that
contains
as a subspace (though the
norm is not a restriction of the
norm).
Example 12 If
with the usual measure, and
, then the function
is in weak
, but not strong
. It is also not in strong or weak
for any other
. But the “local” component
of
is in strong and weak
for all
, and the “global” component
of
is in strong and weak
for all
.
Exercise 13 For any
and
, define the (dyadic) Lorentz norm
to be
norm of the sequence
, and define the Lorentz space
be the space of functions
with
finite, modulo almost everywhere equivalence. Show that
is a quasi-normed space, which is equivalent to
when
and to
when
. Lorentz spaces arise naturally in more refined applications of the real interpolation method, and are useful in certain “endpoint” estimates that fail for Lebesgue spaces, but which can be rescued by using Lorentz spaces instead. However, we will not pursue these applications in detail here.
Exercise 14 Let
be a finite set with counting measure, and let
be a function. For any
, show that
(Hint: to prove the second inequality, normalise
, and then manually dispose of the regions of
where
is too large or too small.) Thus, in some sense, weak
and strong
are equivalent “up to logarithmic factors”.
One can interpolate weak bounds just as one can strong
bounds: if
and
, then
for all . Indeed, from the hypotheses we have
and
for all , and hence by scalar interpolation (using an interpolation parameter
defined by
, and after doing some algebra) we have
As remarked in the previous section, we can improve upon (11); indeed, if we define to be the unique value of
where
and
are equal, then we have
for some depending on
. Inserting this improved bound into (9) we see that we can improve the weak-type bound (10) to a strong-type bound
for some constant . Note that one cannot use the tensor power trick this time to eliminate the constant
as the weak
norms do not behave well with respect to tensor product. Indeed, the constant
must diverge to infinity in the limit
if
, otherwise it would imply that the
norm is controlled by the
norm, which is false by Example 12; similarly one must have a divergence as
if
.
Exercise 15 Let
and
. Refine the inclusions in (8) to
Define the strong type diagram of a function to be the set of all
for which
lies in strong
, and the weak type diagram to be the set of all
for which
lies in weak
. Then both the strong and weak type diagrams are connected subsets of
, and the strong type diagram is contained in the weak type diagram, and contains in turn the interior of the weak type diagram. By experimenting with linear combinations of the examples in Example 12 we see that this is basically everything one can say about the strong and weak type diagrams, without further information on
or
.
Exercise 16 Let
be a measurable function which is finite almost everywhere. Show that there exists a unique non-increasing left-continuous function
such that
for all
, and in particular
for all
, and
. (Hint: first look for the formula that describes
for some
in terms of
.) The function
is known as the non-increasing rearrangement of
, and the spaces
and
are examples of rearrangement-invariant spaces. There are a class of useful rearrangement inequalities that relate
to its rearrangements, and which can be used to clarify the structure of rearrangement-invariant spaces, but we will not pursue this topic here.
Exercise 17 Let
be a
-finite measure space, let
, and
be a measurable function. Show that the following are equivalent:
lies in
, thus
for some finite
.
- There exists a constant
such that
for all sets
of finite measure.
Furthermore show that the best constants
in the above statements are equivalent up to multiplicative constants depending on
, thus
. Conclude that the modified weak
norm
, where
ranges over all sets of positive finite measure, is a genuine norm on
which is equivalent to the
quasinorm.
Exercise 18 Let
be an integer. Find a probability space
and functions
with
for
such that
for some absolute constant
. (Hint: exploit the logarithmic divergence of the harmonic series
.) Conclude that there exists a probability space
such that the
quasi-norm is not equivalent to an actual norm.
Exercise 19 Let
be a
-finite measure space, let
, and
be a measurable function. Show that the following are equivalent:
lies in
.
- There exists a constant
such that for every set
of finite measure, there exists a subset
with
such that
.
Exercise 20 Let
be a measure space of finite measure, and
be a measurable function. Show that the following two statements are equivalent:
- There exists a constant
such that
for all
.
- There exists a constant
such that
.
— 3. Interpolation of operators —
We turn at last to the central topic of these notes, which is interpolation of operators between functions on two fixed measure spaces
and
. To avoid some (very minor) technicalities we will make the mild assumption throughout that
and
are both
-finite, although much of the theory here extends to the non-
-finite setting.
A typical situation is that of a linear operator which maps one
space to another
, and also maps
to
for some exponents
; thus (by linearity)
will map the larger vector space
to
, and one has some estimates of the form
for all respectively, and some
. We would like to then interpolate to say something about how
maps
to
.
The complex interpolation method gives a satisfactory result as long as the exponents allow one to use duality methods, a result known as the Riesz-Thorin theorem:
Theorem 21 (Riesz-Thorin theorem) Let
and
. Let
be a linear operator obeying the bounds (13), (14) for all
respectively, and some
. Then we have
for all
and
, where
,
, and
.
Remark 22 When
is a point, this theorem essentially collapses to Lemma 9 (and when
is a point, this is a dual formulation of that lemma); and when
and
are both points; this collapses to interpolation of scalars.
Proof: If then the claim follows from Lemma 9, so we may assume
, which in particular forces
to be finite. By symmetry we can take
. By multiplying the measures
and
(or the operator
) by various constants, we can normalise
(the case when
or
is trivial). Thus we have
also.
By Hölder’s inequality, the bound (13) implies that
for all and
, where
is the dual exponent of
. Similarly we have
for all ,
that are simple functions with finite measure support. To see this, we first normalise
. Observe that we can write
,
for some functions
of magnitude at most
. If we then introduce the quantity
(with the conventions that in the endpoint case
) we see that
is a holomorphic function of
of at most exponential growth which equals
when
. When instead
, an application of (15) shows that
; a similar claim obtains when
using (16). The claim now follows from Theorem 4.
The estimate (17) has currently been established for simple functions with finite measure support. But one can extend the claim to any
(keeping
simple with finite measure support) by decomposing
into a bounded function and a function of finite measure support, approximating the former in
by simple functions of finite measure support, and approximating the latter in
by simple functions of finite measure support, and taking limits using (15), (16) to justify the passage to the limit. One can then also allow arbitrary
by using the monotone convergence theorem. The claim now follows from the duality between
and
.
Suppose one has a linear operator that maps simple functions of finite measure support on
to measurable functions on
(modulo almost everywhere equivalence). We say that such an operator is of strong type
if it can be extended in a continuous fashion to an operator on
to an operator on
; this is equivalent to having an estimate of the form
for all simple functions
of finite measure support. (The extension is unique if
is finite or if
has finite measure, due to the density of simple functions of finite measure support in those cases. Annoyingly, uniqueness fails for
of an infinite measure space, though this turns out not to cause much difficulty in practice, as the conclusions of interpolation methods are usually for finite exponents
.) Define the strong type diagram to be the set of all
such that
is of strong type
. The Riesz-Thorin theorem tells us that if
is of strong type
and
with
and
, then
is also of strong type
for all
; thus the strong type diagram contains the closed line segment connecting
with
. Thus the strong type diagram of
is convex in
at least. (As we shall see later, it is in fact convex in all of
.) Furthermore, on the intersection of the strong type diagram with
, the operator norm
is a log-convex function of
.
Exercise 23 If
with the usual measure, show that the strong type diagram of the identity operator is the triangle
. If instead
with the usual counting measure, show that the strong type diagram of the identity operator is the triangle
. What is the strong type diagram of the identity when
with the usual measure?
Exercise 24 Let
(resp.
) be a linear operator from simple functions of finite measure support on
(resp.
) to measurable functions on
(resp.
) modulo a.e. equivalence that are absolutely integrable on finite measure sets. We say
are formally adjoint if we have
for all simple functions
of finite measure support on
respectively. If
, show that
is of strong type
if and only if
is of strong type
. Thus, taking formal adjoints reflects the strong type diagram around the line of duality
, at least inside the Banach space region
.
Remark 25 There is a powerful extension of the Riesz-Thorin theorem known as the Stein interpolation theorem, in which the single operator
is replaced by a family of operators
for
that vary holomorphically in
in the sense that
is a holomorphic function of
for any sets
of finite measure. Roughly speaking, the Stein interpolation theorem asserts that if
is of strong type
for
with a bound growing at most exponentially in
, and
itself grows at most exponentially in
in some sense, then
will be of strong type
. A precise statement of the theorem and some applications can be found in Stein’s book on harmonic analysis.
Now we turn to the real interpolation method. Instead of linear operators, it is now convenient to consider sublinear operators mapping simple functions
of finite measure support in
to
-valued measurable functions on
(modulo almost everywhere equivalence, as usual), obeying the homogeneity relationship
and the pointwise bounds
and
for all , and all simple functions
of finite measure support.
Every linear operator is sublinear; also, the absolute value of a linear (or sublinear) operator is also sublinear. More generally, any maximal operator of the form
, where
is a family of sub-linear operators, is also a non-negative sublinear operator; note that one can also replace the supremum here by any other norm in
, e.g. one could take an
norm
for any
. (After
and
, a particularly common case is when
, in which case
is known as a square function.)
The basic theory of sublinear operators is similar to that of linear operators in some respects. For instance, continuity is still equivalent to boundedness:
Exercise 26 Let
be a sublinear operator, and let
. Assume that either
is finite, or
has finite measure. Then the following are equivalent:
can be extended to a continuous operator from
to
.
- There exists a constant
such that
for all simple functions
of finite measure support.
can be extended to a operator from
to
such that
for all
and some
.
Show that the extension mentioned above is unique. Finally, show that the same equivalences hold if
is replaced by
throughout.
We say that is of strong type
if any of the above equivalent statements (for
) hold, and of weak type
if any of the above equivalent statements (for
) hold. We say that a linear operator
is of strong or weak type
if its non-negative counterpart
is; note that this is compatible with our previous definition of strong type for such operators. Also, Chebyshev’s inequality tells us that strong type
implies weak type
.
We now give the real interpolation counterpart of the Riesz-Thorin theorem, namely the Marcinkeiwicz interpolation theorem:
Theorem 27 (Marcinkiewicz interpolation theorem) Let
and
be such that
, and
for
. Let
be a sublinear operator which is of weak type
and of weak type
. Then
is of strong type
.
Remark 28 Of course, the same claim applies to linear operators
by setting
. One can also extend the argument to quasilinear operators, in which the pointwise bound
is replaced by
for some constant
, but this generalisation only appears occasionally in applications. The conditions
can be replaced by the variant condition
(see Exercise 31, Exercise 33), but cannot be eliminated entirely: see Exercise 32. The precise hypotheses required on
are rather technical and I recommend that they be ignored on a first reading.
Proof: For notational reasons it is convenient to take finite; however the arguments below can be modified without much difficulty to deal with the infinite case (or one can use a suitable limiting argument); we leave this to the interested reader.
By hypothesis, there exist constants such that
for all simple functions of finite measure support, and all
. Let us write
to denote
for some constant
depending on the indicated parameters. By (9), it will suffice to show that
By homogeneity we can normalise .
Actually, it will be more slightly convenient to work with the dyadic version of the above estimate, namely
see Exercise 11. The hypothesis similarly implies that
The basic idea is then to get enough control on the numbers in terms of the numbers
that one can deduce (20) from (21).
When , the claim follows from direct substitution of (18), (19) (see also the discussion in the previous section about interpolating strong
bounds from weak ones), so let us assume
; by symmetry we may take
, and thus
. In this case we cannot directly apply (18), (19) because we only control
in
, not
or
. To get around this, we use the basic real interpolation trick of decomposing
into pieces. There are two basic choices for what decomposition to pick. On one hand, one could adopt a “minimalistic” approach and just decompose into two pieces
where and
, and the threshold
is a parameter (depending on
) to be optimised later. Or we could adopt a “maximalistic” approach and perform the dyadic decomposition
where . (Note that only finitely many of the
are non-zero, as we are assuming
to be a simple function.) We will adopt the latter approach, in order to illustrate the dyadic decomposition method; the former approach also works, but we leave it as an exercise to the interested reader.
From sublinearity we have the pointwise estimate
which implies that
whenever are positive constants such that
, but for which we are otherwise at liberty to choose. We will set aside the problem of deciding what the optimal choice of
is for now, and continue with the proof.
From (18), (19), we have two bounds for the quantity , namely
and
From construction of we can bound
and similarly for , and thus we have
for . To prove (20), it thus suffices to show that
It is convenient to introduce the quantities appearing in (21), thus
and our task is to show that
Since , we have
, and so we are reduced to the purely numerical task of locating constants
with
for all
such that
We can simplify this expression a bit by collecting terms and making some substitutions. The points are collinear, and we can capture this by writing
for some and some
. We can then simplify the left-hand side of (22) to
Note that is positive and
is negative. If we then pick
to be a sufficiently small multiple of
where
(say), we obtain the claim by summing geometric series.
Remark 29 A closer inspection of the proof (or a rescaling argument to reduce to the normalised case
, as in preceding sections) reveals that one establishes the estimate
for all simple functions
of finite measure support (or for all
, if one works with the continuous extension of
to such functions), and some constant
. Thus the conclusion here is weaker by a multiplicative constant from that in the Riesz-Thorin theorem, but the hypotheses are weaker too (weak-type instead of strong-type). Indeed, we see that the constant
must blow up as
or
.
The power of the Marcinkiewicz interpolation theorem, as compared to the Riesz-Thorin theorem, is that it allows one to weaken the hypotheses on from strong type to weak type. Actually, it can be weakened further. We say that a non-negative sublinear operator
is restricted weak-type
for some
if there is a constant
such that
for all sets of finite measure and all simple functions
with
. Clearly restricted weak-type
is implied by weak-type
, and thus by strong-type
. (One can also define the notion of restricted strong-type
by replacing
with
; this is between strong-type
and restricted weak-type
, but is incomparable to weak-type
.)
Exercise 30 Show that the Marcinkiewicz interpolation theorem continues to hold if the weak-type hypotheses are replaced by restricted weak-type hypothesis. (Hint: where were the weak-type hypotheses used in the proof?)
We thus see that the strong-type diagram of contains the interior of the restricted weak-type or weak-type diagrams of
, at least in the triangular region
.
Exercise 31 Suppose that
is a sublinear operator of restricted weak-type
and
for some
. Show that
is of restricted weak-type
for any
, or in other words the restricted type diagram is convex in
. (This is an easy result requiring only interpolation of scalars.) Conclude that the hypotheses
in the Marcinkiewicz interpolation theorem can be replaced by the variant
.
Exercise 32 For any
, let
be the natural numbers
with the weighted counting measure
, thus each point
has mass
. Show that if
, then the identity operator from
to
is of weak-type
but not strong-type
when
and
. Conclude that the hypotheses
cannot be dropped entirely.
Exercise 33 Suppose we are in the situation of the Marcinkiewicz interpolation theorem, with the hypotheses
replaced by
. Show that for all
and
there exists a
such that
for all simple functions
of finite measure support, where the Lorentz norms
were defined in Exercise 13. (Hint: repeat the proof of the Marcinkiewicz interpolation theorem, but partition the sum
into regions of the form
for integer
. Obtain a bound for each summand which decreases geometrically as
.) Conclude that the hypotheses
in the Marcinkiewicz interpolation theorem can be replaced by
. This Lorentz space version of the interpolation theorem is in some sense the “right” version of the theorem, but the Lorentz spaces are slightly more technical to deal with than the Lebesgue spaces, and the Lebesgue space version of Marcinkiewicz interpolation is largely sufficient for most applications.
Exercise 34 For
, let
be
-finite measure spaces, and let
be a linear operator from simple functions of finite measure support on
to measurable functions on
(modulo almost everywhere equivalence, as always). Let
,
be the product spaces (with product
-algebra and product measure). Show that there exists a unique (modulo a.e. equivalence) linear operator
defined on linear combinations of indicator functions
of product sets of sets
,
of finite measure, such that
for a.e.
; we refer to
as the tensor product of
and
and write
. Show that if
are of strong-type
for some
with operator norms
respectively, then
can be extended to a bounded linear operator on
to
with operator norm exactly equal to
, thus
(Hint: for the lower bound, show that
for all simple functions
. For the upper bound, express
as the composition of two other operators
and
for some identity operators
, and establish operator norm bounds on these two operators separately.) Use this and the tensor power trick to deduce the Riesz-Thorin theorem (in the special case when
for
, and
) from the Marcinkiewicz interpolation theorem. Thus one can (with some effort) avoid the use of complex variable methods to prove the Riesz-Thorin theorem, at least in some cases.
Exercise 35 (Hölder’s inequality for Lorentz spaces) Let
and
for some
. Show that
, where
and
, with the estimate
for some constant
. (This estimate is due to O’Neil.)
Remark 36 Just as interpolation of functions can be clarified by using step functions
as a test case, it is instructive to use rank one operators such as
where
are finite measure sets, as test cases for the real and complex interpolation methods. (After understanding the rank one case, I then recommend looking at the rank two case, e.g.
, where
could be very different in size from
.)
— 4. Some examples of interpolation —
Now we apply the interpolation theorems to some classes of operators. An important such class is given by the integral operators
from functions to functions
, where
is a fixed measurable function, known as the kernel of the integral operator
. Of course, this integral is not necessarily convergent, so we will also need to study the sublinear analogue
which is well-defined (though it may be infinite).
The following useful lemma gives us strong-type bounds on and hence
, assuming certain
type bounds on the rows and columns of
.
Lemma 37 (Schur’s test) Let
be a measurable function obeying the bounds
for almost every
, and
for almost every
, where
and
. Then for every
,
and
are of strong-type
, with
well-defined for all
and almost every
, and furthermore
Here we adopt the convention that
and
, thus
and
.
Proof: The hypothesis , combined with Minkowski’s integral inequality, shows us that
for all ; in particular, for such
,
is well-defined almost everywhere, and
Similarly, Hölder’s inequality tells us that for ,
is well-defined everywhere, and
Applying the Riesz-Thorin theorem we conclude that
for all simple functions with finite measure support; replacing
with
we also see that
for all simple functions with finite measure support, and thus (by monotone convergence) for all
. The claim then follows.
Example 38 Let
be a matrix such that the sum of the magnitudes of the entries in every row and column is at most
, i.e.
for all
and
for all
. Then one has the bound
for all vectors
and all
. Note the extreme cases
,
can be seen directly; the remaining cases then follow from interpolation.
A useful special case arises when
is an
-sparse matrix, which means that at most
entries in any row or column are non-zero (e.g. permutation matrices are
-sparse). We then conclude that the
operator norm of
is at most
.
Exercise 39 Establish Schur’s test by more direct means, taking advantage of the duality relationship
for
, as well as Young’s inequality
for
. (You may wish to first work out Example 38, say with
, to figure out the logic.)
A useful corollary of Schur’s test is Young’s convolution inequality for the convolution of two functions
,
, defined as
provided of course that the integrand is absolutely convergent.
Exercise 40 (Young’s inequality) Let
be such that
. Show that if
and
, then
is well-defined almost everywhere and lies in
, and furthermore that
(Hint: Apply Schur’s test to the kernel
.)
Remark 41 There is nothing special about
here; one could in fact use any locally compact group
with a bi-invariant Haar measure. On the other hand, if one specialises to
, then it is possible to improve Young’s inequality slightly, to
where
, a result of Beckner; the constant here is best possible, as can be seen by testing the inequality in the case when
are Gaussians.
Exercise 42 Let
, and let
,
. Young’s inequality tells us that
. Refine this further by showing that
, i.e.
is continuous and goes to zero at infinity. (Hint: first show this when
, then use a limiting argument.)
We now give a variant of Schur’s test that allows for weak estimates.
Lemma 43 (Weak-type Schur’s test) Let
be a measurable function obeying the bounds
for almost every
, and
for almost every
, where
and
(note the endpoint exponents
are now excluded). Then for every
,
and
are of strong-type
, with
well-defined for all
and almost every
, and furthermore
Here we again adopt the convention that
and
.
Proof: From Exercise 17 we see that
for any measurable , where we use
to denote
for some
depending on the indicated parameters. By the Fubini-Tonelli theorem, we conclude that
for any ; by Exercise 17 again we conclude that
thus is of weak-type
. In a similar vein, from yet another application of Exercise 17 we see that
whenever and
has finite measure; thus
is of restricted type
. Applying Exercise 30 we conclude that
is of strong type
(with operator norm
), and the claim follows.
This leads to a weak-type version of Young’s inequality:
Exercise 44 (Weak-type Young’s inequality) Let
be such that
. Show that if
and
, then
is well-defined almost everywhere and lies in
, and furthermore that
for some constant
.
Exercise 45 Refine the previous exercise by replacing
with the Lorentz space
throughout.
Recall that the function will lie in
for
. We conclude
Corollary 46 (Hardy-Littlewood-Sobolev fractional integration inequality) Let
and
be such that
. If
, then the function
, defined as
is well-defined almost everywhere and lies in
, and furthermore that
for some constant
.
This inequality is of importance in the theory of Sobolev spaces, which we will discuss in a subsequent lecture.
Exercise 47 Show that Corollary 46 can fail at the endpoints
,
, or
.
Update, Apr 6: another exercise added; note renumbering.
Update, Apr 8: some formatting errors fixed.
Update, Sep 14: definition of sublinearity fixed.

137 comments
Comments feed for this article
4 April, 2010 at 8:22 am
pavel zorin
Dear Prof. Tao,
some errata for your proof of the Marcinkiewicz interpolation theorem:
In equation (22), there should be no summation over m.
In the last equation (“simplify the left-hand side of (22) to…”), the summation goes over n instead of m, and the exponent of is
is 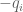 , not
, not 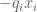 .
.
This affects the choice of the c’s, i.e.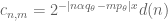 with
with  would do. The normalization sequence satisfies $d(n) = O(1)$ automatically given
would do. The normalization sequence satisfies $d(n) = O(1)$ automatically given 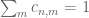 .
.
I also wonder whether, at the end of the proof of the Riesz-Thorin theorem, the decomposition of f into a bounded and a finitely supported function could be omitted in case (when the sum of the norms of the components is greater then the norm of f itself). It does provide continuity of
(when the sum of the norms of the components is greater then the norm of f itself). It does provide continuity of 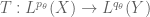 (with norm 2), so that the conclusion follows because it actually has norm 1 on a dense subspace (of simple functions), but can one do without it?
(with norm 2), so that the conclusion follows because it actually has norm 1 on a dense subspace (of simple functions), but can one do without it?
best regards, pavel
4 April, 2010 at 9:21 am
Terence Tao
Thanks for the correction!
One can try to extend the main argument directly to general functions rather than just to simple functions with finite measure support; from a conceptual viewpoint this is more natural, but from a technical viewpoint it basically requires one to establish the continuity of
functions rather than just to simple functions with finite measure support; from a conceptual viewpoint this is more natural, but from a technical viewpoint it basically requires one to establish the continuity of  to
to 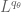 beforehand to justify various formal operations, which is inconvenient as this is part of what one is trying to prove in the first place.
beforehand to justify various formal operations, which is inconvenient as this is part of what one is trying to prove in the first place.
7 April, 2010 at 2:13 pm
pavel zorin
Dear Prof. Tao,
I am experiencing slight difficulties with Exercise 21 (Marcinkiewicz theorem, Lorentz space version).
Doing the same calculations as in the given proof of the special case, I obtain (this time with and
and 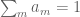 ), as a sufficient condition the existence of summable (over m) c’s such that
), as a sufficient condition the existence of summable (over m) c’s such that
 .
.
Now, assuming the easiest case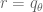 , the exponent of
, the exponent of  is less than 1 for one of the i's (unless
is less than 1 for one of the i's (unless  ). Even then, I could not think of an approach to finding c's that uses all the information: whatever I came up with looked like it would work without any assumptions on a's and was therefore false. Could you give some further indications?
). Even then, I could not think of an approach to finding c's that uses all the information: whatever I came up with looked like it would work without any assumptions on a's and was therefore false. Could you give some further indications?
kind regards, pavel
7 April, 2010 at 3:02 pm
Terence Tao
Ah, yes, this is a little delicate, in part because the decomposition of f used here is actually not the optimal one for this problem – it decomposes the height of the function dyadically (vertical dyadic decomposition), when in fact it is the width
of the function dyadically (vertical dyadic decomposition), when in fact it is the width 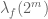 that ought to be dyadically decomposed (horizontal dyadic decomposition). One can still recover from this point by decomposing the sequence
that ought to be dyadically decomposed (horizontal dyadic decomposition). One can still recover from this point by decomposing the sequence  into dyadic pieces, but this is quite messy.
into dyadic pieces, but this is quite messy.
Another approach is to use frequency envelopes. Pick a small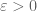 and replace
and replace  by the slightly larger envelope
by the slightly larger envelope  . The point of doing so is that the
. The point of doing so is that the  obey a Lipschitz property
obey a Lipschitz property 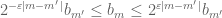 but are still summable in
but are still summable in 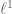 . One then chooses
. One then chooses  to be adapted to the crossover point between the two quantities in the
to be adapted to the crossover point between the two quantities in the 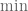 (modifying the
(modifying the 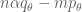 term by some multiple of
term by some multiple of 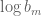 ); as long as the Lipschitz parameter
); as long as the Lipschitz parameter  is small enough, one will still be able to close the argument.
is small enough, one will still be able to close the argument.
I may elaborate on the frequency envelope approach in a subsequent blog post.
14 April, 2011 at 4:28 pm
Wenying Gan
Dear Prof. Tao:
I think there is a typo in $Ex 8$. There should be a index 1/p for log(1+|X|). Or the result we need to prove is incorrect. Thanks in advance.
Best
Wenying Gan
[Corrected, thanks – T.]
4 November, 2012 at 6:13 pm
Gandhi Viswanathan
Dear Professor Tao,
The “Control Level Sets” tricki page you cite earlier also lacks the (1/p) index mentioned in this comment about Ex 8. Can we assume the same correction is needed in the tricki ?
4 November, 2012 at 6:21 pm
Terence Tao
Yes; I edited the tricki page accordingly.
4 November, 2012 at 6:49 pm
Gandhi Viswanathan
Thanks!
3 May, 2011 at 6:22 pm
Stein’s interpolation theorem « What’s new
[…] where are functions depending on in a suitably analytic manner, for instance taking for some test function , and similarly for . If are chosen properly, will depend analytically on as well, and the two hypotheses (1), (2) give bounds on and for respectively. The Lindelöf theorem then gives bounds on intermediate values of , such as ; and the Riesz-Thorin theorem can then be deduced by a duality argument. (This is covered in many graduate real analysis texts; I myself covered it here.) […]
4 April, 2012 at 12:50 am
X
Dear Prof. Tao, is very small, then if
is very small, then if  , then the bound goes to
, then the bound goes to  . So I think the theorem doesn’t cover directly the case where the bound is, for example,
. So I think the theorem doesn’t cover directly the case where the bound is, for example,  .
.
There is one thing unclear for me In your statement of Lindelof’s Theorem. Suppose
Could you please help explain a bit?
Thank you!
X
4 April, 2012 at 7:14 am
Terence Tao
The factor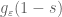 will damp out the growth as
will damp out the growth as 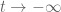 .
.
31 October, 2012 at 9:10 am
Gandhi Viswanathan
Dear Professor Tao, I noticed that the quantity defined via
defined via  in the complex analysis (4th) proof of Lemma 2 above is identical to the quantity
in the complex analysis (4th) proof of Lemma 2 above is identical to the quantity  defined below Lemma 2 in the 2nd proof (via Jensen’s inequality).
defined below Lemma 2 in the 2nd proof (via Jensen’s inequality).
4 March, 2013 at 3:13 pm
Lior Silberman
In Remark 2, should be
should be 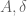 .
.
[Corrected, thanks – T.]
23 September, 2013 at 10:54 am
Anonymous
Dear Professor Tao,
I was wandering if for $p1$ such that $\frac{1}{p}+\frac{1}{q}=2$ one has a young type inequality for the convolution. That is $||f*g||_{1}\leq C||f||_{p} ||g||_{q}$
Thanks!
27 April, 2014 at 12:34 pm
Fan
For remark 8, is it necessary that the Haar measure is “bi”-invariant? Is the commutativity of the convolution implicitly used anywhere?
27 April, 2014 at 2:02 pm
Terence Tao
The bi-invariance of Haar measure is needed in order to ensure the map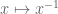 is measure-preserving, otherwise one has to be very careful how to define convolution, as various definitions of convolution that are equivalent in the bi-invariant setting may now cease to be equivalent.
is measure-preserving, otherwise one has to be very careful how to define convolution, as various definitions of convolution that are equivalent in the bi-invariant setting may now cease to be equivalent.
27 April, 2014 at 2:20 pm
Fan
Thanks.
5 May, 2014 at 6:49 am
urbano
Dear Professor Tao,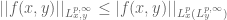 ?
?
is it also possible to show that
4 February, 2015 at 3:40 am
Felix V.
Dear Prof. Tao, thanks for the nice post.
One small comment: In equation (7) in the statement of Lindelöf’s theorem, I believe you want to put |t| instead of t in the exponent of the right hand side. Otherwise, the theorem still holds true, but the statement is needlessly weak.
Best regards, Felix V.
[Corrected, thanks – T.]
19 February, 2015 at 4:36 am
Felix V.
Dear Prof. Tao,
I think I found a problem in Exercise 17: For sublinear operators,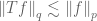
 .
.
it seems that “boundedness” in the sense of
for all step functions does not(!) imply that T can be extended
continuously to all of
My counterexample is the following: Define for simple functions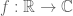

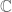 can be regarded as an
can be regarded as an  -space on a singleton
-space on a singleton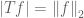 ,
,
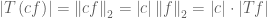

Here,
set. For simple functions, Tf is indeed well-defined with
which implies
and
so that T is indeed sublinear and “bounded”.
But T itself is not continuous (and thus admits no continuous extension)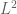 -norm: If we take
-norm: If we take ![f:=\chi_{\left[0,1\right]}](https://s0.wp.com/latex.php?latex=f%3A%3D%5Cchi_%7B%5Cleft%5B0%2C1%5Cright%5D%7D&bg=ffffff&fg=545454&s=0&c=20201002)
![f_{n}:=\chi_{\left[0,1\right]}+\frac{1}{n}\chi_{\left[10+n,10+2n\right]}](https://s0.wp.com/latex.php?latex=f_%7Bn%7D%3A%3D%5Cchi_%7B%5Cleft%5B0%2C1%5Cright%5D%7D%2B%5Cfrac%7B1%7D%7Bn%7D%5Cchi_%7B%5Cleft%5B10%2Bn%2C10%2B2n%5Cright%5D%7D&bg=ffffff&fg=545454&s=0&c=20201002) ,
,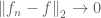 , but $Tf=e^{i\pi}\left\Vert f\right\Vert _{2}=-1$ and
, but $Tf=e^{i\pi}\left\Vert f\right\Vert _{2}=-1$ and 
 .
.
with respect to the
and
then
for
Best regards, Felix V.
19 February, 2015 at 4:40 am
Felix V.
Oh, I just noted that you require to have values in
to have values in ![[0,\infty]](https://s0.wp.com/latex.php?latex=%5B0%2C%5Cinfty%5D&bg=ffffff&fg=545454&s=0&c=20201002) . But you also claim that every linear operator is sublinear, which certainly does not hold if we require values in
. But you also claim that every linear operator is sublinear, which certainly does not hold if we require values in ![[0,\infty]](https://s0.wp.com/latex.php?latex=%5B0%2C%5Cinfty%5D&bg=ffffff&fg=545454&s=0&c=20201002) .
.
19 February, 2015 at 9:56 am
Terence Tao
Sorry, there was an additional hypothesis in the definition of sublinearity (namely that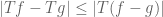 ) that was not corrected in the post (though it was noted in the errata for the published version of these notes).
) that was not corrected in the post (though it was noted in the errata for the published version of these notes).
25 November, 2015 at 10:07 am
Anon
Typo? In Riesz-Thorin Theorem missing parantheses around 1-\theta?
[Corrected, thanks – T.]
2 December, 2015 at 12:06 am
Anonymous
Dear Prof. Tao,
I guess that in Lemma 9, $p$ and $L^p(X)$ should be replaced by $p_\theta$ and $L^{p_\theta}(X)$, resp.
[Actually, I prefer to leave the qualitative portion of the lemma (which I presume is the part you are referring to) in terms of a parameter instead of a
parameter instead of a  parameter, as the latter is only useful for the quantitative estimate. -T.]
parameter, as the latter is only useful for the quantitative estimate. -T.]
11 December, 2015 at 5:19 pm
Anonymous
About Exercise 16,
I think Exercise 16 should be corrected a little bit. If substitute t with 0 and f*(0) respectively, we might have the measure of X is infinite and ||f||_{inf}<= f*(0)
http://math.stackexchange.com/questions/257365/questions-related-to-distribution-function-and-its-inverse
In this site, altering some of the definitions and conditions makes things going well.
It would be appreciated if you check.
[The case should not have been present and is now deleted – T.]
case should not have been present and is now deleted – T.]
12 December, 2015 at 3:55 am
Anonymous
Dear Prof. Tao,
In Exercise 17, is p` is the dual exponent of p?
[Corrected, thanks – T.]
26 December, 2015 at 4:52 pm
Jiwoong Jang
Dear Prof. Tao,
In the exercise about the marcinkiewicz theorem on the Lorentz spaces, I see your point that adopting the frequency envelope b_m of a_m works, but only in the particular case of $r<=q_\theta$. If r is large, I still do not know how to eliminate the r portion of the exponent of b_m.
Could you give me a direction to go? Or, Is it enough to prove all the things? I`m now considering the quasi-metric structure of $l^{q_\theta/r}(\mathbb{Z})$.
Best
Jang
1 June, 2016 at 6:58 pm
Anonymous
… from the calculus identity
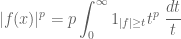
and the Fubini-Tonelli theorem, we obtain the formula…
Some typo here? The left hand side is a function in while the right hand side is a number?
while the right hand side is a number?
[The on the RHS should be
on the RHS should be  , now fixed – T.]
, now fixed – T.]
27 June, 2016 at 9:08 am
Benson
Dear Prof,
Is there any work done on application of any of the interpolation theorems to signal and image processing . I will like to know.
11 October, 2016 at 6:58 am
Lecture 9. Diffusion semigroups in L^p | Research and Lecture notes
[…] proof of the theorem can be found in this post by […]
3 December, 2016 at 5:10 am
VMT
Hi Professor, with
with  .
. a sufficiently small multiple of
a sufficiently small multiple of  , where
, where  .
.
I have some little corrections to your instructive proof of Marcinkiewicz interpolation:
in (22) there should be only the sum over n.
In the last display of the proof, m should be replaced with n and
I guess one should then take
Finally, there are three references to (16), (19) which should be replaced with (18), (19).
[Corrected, thanks – T.]
23 January, 2017 at 3:41 pm
Anonymous
(1) In Section 3, what is the definition of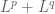 ? Is it the same or different from the “direct sum”?
? Is it the same or different from the “direct sum”?
[No: see https://en.wikipedia.org/wiki/Minkowski_addition – T.]
(2) In Stein and Weiss’s Introduction to Fourier Analysis on Enclidean Spaces, the linear operator in the Riesz-Thorin Theorem is defined on a set of simple functions of sets of finite measures. Are that version equivalent to the one in this note? Is there any historical reason or theoretical convenience in Stein-Weiss’s version?
in the Riesz-Thorin Theorem is defined on a set of simple functions of sets of finite measures. Are that version equivalent to the one in this note? Is there any historical reason or theoretical convenience in Stein-Weiss’s version?
[It makes little difference in practice, since a bounded linear operator on a dense subclass of a normed vector space can always be uniquely extended to a bounded linear operator on the full space. -T.]
25 January, 2017 at 4:37 am
Anonymous
In remark 29 (lines 4 and 7), it seems that the constant (with several subscripts) should not contain the subscript
(with several subscripts) should not contain the subscript  .
.
Is the best possible constant (as a function of its subscripts) known up to a multiplication by an absolute constant?
[Yes – I believe this is discussed for instance in Bergh and Lofstrom. -T.]
21 February, 2017 at 11:13 am
Anonymous
– Right after (6), would you elaborate what the following remark means?
The geometric series formula tells us that such factors are absolutely summable, and so in practice it is often a useful heuristic to pretend that the cases dominate so strongly that the other cases can be viewed as negligible by comparison.
cases dominate so strongly that the other cases can be viewed as negligible by comparison.
Do you have an example when one would like to sum the factors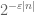 ?
?
– “However, one certainly cannot interpolate lower bounds: (i)lower bounds on a log-convex function {\theta \rightarrow A_\theta} at {\theta=0} and {\theta=1} yield no information about the value of, say, {A_{1/2}}. (ii)Similarly, one cannot extrapolate upper bounds on log-convex functions: an upper bound on, say, {A_0} and {A_{1/2}} does not give any information about {A_1}. (However, an upper bound on {A_0} coupled with a lower bound on {A_{1/2}} gives a lower bound on {A_1}; this is the contrapositive of an interpolation statement.)”
I’m a little confused with this remark. For (i), if one looks at the log-convex function (5), then (3) means one can interpolate lower bounds?
25 February, 2017 at 10:30 am
Terence Tao
See for instance the argument deriving (12) from (11) (here we use a continuous variable instead of a discrete one
instead of a discrete one  , but the principle is the same. See also the proof of Theorem 27.)
, but the principle is the same. See also the proof of Theorem 27.)
The function in (5) is log-convex as well as log-concave, which is why one can interpolate lower bounds for that function. However, most log-concave functions will not be log-convex.
in (5) is log-convex as well as log-concave, which is why one can interpolate lower bounds for that function. However, most log-concave functions will not be log-convex.
21 February, 2017 at 5:20 pm
Anonymous
In the second proof Lemma 9, one can divide by its
by its 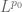 or
or  norm to achieve one of the normalizations. How can one do it simultaneously for both? Why is the measure
norm to achieve one of the normalizations. How can one do it simultaneously for both? Why is the measure  also allowed to change?
also allowed to change?
25 February, 2017 at 10:33 am
Terence Tao
If is a measure space, then so is
is a measure space, then so is 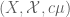 for any
for any  . It is then a simple matter of algebra to find, given any measure space
. It is then a simple matter of algebra to find, given any measure space  and any
and any  in both
in both 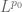 and
and  of that space, constants
of that space, constants  such that
such that  . If we know how to prove Lemma 9 in this case, a little further algebra then recovers Lemma 9 in the general case.
. If we know how to prove Lemma 9 in this case, a little further algebra then recovers Lemma 9 in the general case.
23 February, 2017 at 3:03 pm
Anonymous
In the third proof of Lemma 9, typos in the tensor power:
The component x_m should be x_M and the underlying measure space for the tensor power should be X^M
[Corrected, thanks – T.]
25 February, 2017 at 1:37 pm
Anonymous
One more in
we see from many applications of the Fubini-Tonelli theorem that
the left hand side should be
[Corrected, thanks – T.]
5 March, 2017 at 2:52 pm
Anonymous
In the set of your notes (http://www.math.ucla.edu/~tao/247a.1.06f/notes1.pdf) on harmonic analysis, the first sentence of the introduction to the Vinogradov notation is very confusing (page 5):
In (modified) Vinogradov notation, the notation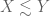 (read:
(read:  is less than or
is less than or ) or
) or  is used synonymously with
is used synonymously with 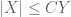 or
or  .
.
comparable to
I think you mean
just as indicated in this post?
[Correction added to 247a page, thanks -T.]
10 March, 2017 at 3:38 pm
Anonymous
In the first proof of Lemma 9, Hölder is used. It is said in your 247a notes 1 that Lemma 9 actually implies Hölder also.
The hint there says that one should consider the convexity of with respect to a measure
with respect to a measure 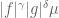 for some constants
for some constants 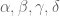 .
.
I don’t understand what this really means. Would you elaborate a little bit more?
[Apply Lemma 9 with replaced by
replaced by 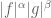 and
and  replaced by
replaced by 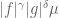 , and for a carefully selected choice of
, and for a carefully selected choice of 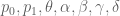 . -T]
. -T]
11 March, 2017 at 5:15 pm
Anonymous
1. Suppose one wants to prove the Holder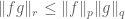 with
with  . Suppose in Lemma 9,
. Suppose in Lemma 9, 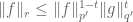 with
with  . One can then choose any
. One can then choose any 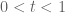 with
with 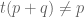 , then let
, then let
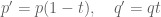

and
The constants do not need to be unique, right?
2. It is said in the hint that one needs to first reduce to the case of finite measure space and and
and  everywhere non-vanishing simple functions. Why is that so? It seems that one can get the proof by directly manipulate the constants so that one can match the exponents of the two inequalities (Holder and the log-convexity).
everywhere non-vanishing simple functions. Why is that so? It seems that one can get the proof by directly manipulate the constants so that one can match the exponents of the two inequalities (Holder and the log-convexity).
[One needs various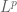 norms to be finite and non-zero in order to justify some algebraic manipulations, such as raising these norms to a negative power. -T]
norms to be finite and non-zero in order to justify some algebraic manipulations, such as raising these norms to a negative power. -T]
17 November, 2017 at 1:11 pm
Anonymous
Why can one replace by
by 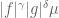 in Lemma 9? Isn’t Lemma 9 only true when one replace
in Lemma 9? Isn’t Lemma 9 only true when one replace  by
by  where
where  is a (nonnegative) constant?
is a (nonnegative) constant?
26 November, 2017 at 10:19 am
Terence Tao
Lemma 9 is true for arbitrary non-negative measures , which gives one the (powerful) freedom to multiply
, which gives one the (powerful) freedom to multiply  by arbitrary non-negative weights, not just constants.
by arbitrary non-negative weights, not just constants.
17 November, 2017 at 1:38 pm
Anonymous
I attempted what was suggested directly:
which seems not quite true…
26 November, 2017 at 10:30 am
Terence Tao
This is a correct inequality. One now has to select the parameters carefully to obtain the desired conclusion.
20 November, 2017 at 6:45 pm
Anonymous
Suppose one wants to prove Hölder for . Assume the log-convexity for
. Assume the log-convexity for 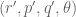 . Apply Lemma 9 with
. Apply Lemma 9 with  replaced by
replaced by 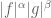 and
and 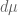 replaced by
replaced by 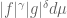 . Comparing the exponents, we want
. Comparing the exponents, we want

So if we let such that
such that 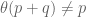 and
and
![\displaystyle r'=r,\ \ p'=(1-\theta)p,\ \ q'=\theta q\\ \alpha = \frac{p}{[(1-\theta)p-\theta q]}\\ \beta = \frac{q}{\theta q-(1-\theta)p}\\ \delta = -\beta p'\\ \gamma = -\alpha q'](https://s0.wp.com/latex.php?latex=%5Cdisplaystyle+r%27%3Dr%2C%5C+%5C+p%27%3D%281-%5Ctheta%29p%2C%5C+%5C+q%27%3D%5Ctheta+q%5C%5C+%5Calpha+%3D+%5Cfrac%7Bp%7D%7B%5B%281-%5Ctheta%29p-%5Ctheta+q%5D%7D%5C%5C+%5Cbeta+%3D+%5Cfrac%7Bq%7D%7B%5Ctheta+q-%281-%5Ctheta%29p%7D%5C%5C+%5Cdelta+%3D+-%5Cbeta+p%27%5C%5C+%5Cgamma+%3D+-%5Calpha+q%27+&bg=ffffff&fg=545454&s=0&c=20201002)
then we have the desired result.
Where one needs to first reduce to the case of finite measure space and f and g everywhere non-vanishing simple functions?
26 November, 2017 at 10:31 am
Terence Tao
If some of the exponents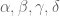 are negative, you will have a division by zero problem if one did not prepare in advance by reducing to the case when
are negative, you will have a division by zero problem if one did not prepare in advance by reducing to the case when 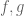 were everywhere non-vanishing.
were everywhere non-vanishing.
10 March, 2017 at 4:39 pm
Anonymous
In 247a notes 1 Problem 5.9, it is said that one can differentiate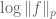 twice with respect to
twice with respect to 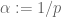 to get the log convexity of the
to get the log convexity of the 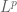 norm. Why should one use
norm. Why should one use 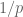 instead of
instead of  ?
?
[The function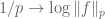 is convex, but the function
is convex, but the function  is usually not convex. -T.]
is usually not convex. -T.]
10 March, 2017 at 4:43 pm
Anonymous
As it is mentioned in the notes, this approach is messy. Has anyone performed the calculation ever to show that this is indeed doable? (Lots of terms would appear when calculating the second derivative. Still possible to see that the second derivative is positive?)
13 March, 2017 at 7:32 am
Anonymous
Another version of (7) in Theorem is given in the 247a notes 1:
Are these two versions equivalent? (Since it could be that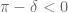 and a positive constant is missing in front of the "inner" exponential function in (7), I'm not sure about this.)
and a positive constant is missing in front of the "inner" exponential function in (7), I'm not sure about this.)
[Yes, they are equivalent. Note that one has the freedom to reduce if desired, in particular one can assume that
if desired, in particular one can assume that 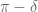 is positive. -T]
is positive. -T]
13 March, 2017 at 10:45 am
Anonymous
According to this set of notes
holomorphic functions are defined on open subsets of . What does the function
. What does the function  being holomorphic on the strip
being holomorphic on the strip  (which is closed) mean? (What does one mean that
(which is closed) mean? (What does one mean that  is holomorphic on the boundary?)
is holomorphic on the boundary?)
[It means that the function extends to be holomorphic on some open neighbourhood of the strip. -T]
13 March, 2017 at 11:43 am
Anonymous
In the proof of Theorem 4, would you elaborate why is the function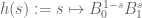 holomorphic and non-zero on
holomorphic and non-zero on  ?
?
Isn’t it true that one needs to define using the complex logarithm, which is not holomorphic at
using the complex logarithm, which is not holomorphic at 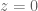 ? Moreover, what branch one needs to use for the function
? Moreover, what branch one needs to use for the function  ?
?
[One only needs to take logarithms of the positive real constants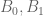 ; at no point does one need to take logarithms of the complex variable
; at no point does one need to take logarithms of the complex variable  . -T]
. -T]
17 March, 2017 at 7:37 am
Anonymous
In the last step of passage to the limit of Theorem 21 (Riesz-Thorin theorem), one decomposes into a bounded function and a function of finite measure support and then approximates each piece by simple functions. How would one put the two approximations together to get the approximation for
into a bounded function and a function of finite measure support and then approximates each piece by simple functions. How would one put the two approximations together to get the approximation for  ?
?
18 March, 2017 at 6:37 am
Anonymous
In Lemma 9 and Theorem 21; the exponents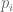 are in
are in ![[0,\infty]](https://s0.wp.com/latex.php?latex=%5B0%2C%5Cinfty%5D&bg=ffffff&fg=545454&s=0&c=20201002) while the
while the 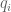 are in
are in ![[1,\infty]](https://s0.wp.com/latex.php?latex=%5B1%2C%5Cinfty%5D&bg=ffffff&fg=545454&s=0&c=20201002) . Can we change the range for
. Can we change the range for 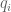 to be also in
to be also in ![[0,\infty]](https://s0.wp.com/latex.php?latex=%5B0%2C%5Cinfty%5D&bg=ffffff&fg=545454&s=0&c=20201002) ? (Or is there a typo so that the
? (Or is there a typo so that the 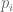 should also in
should also in ![[1,\infty]](https://s0.wp.com/latex.php?latex=%5B1%2C%5Cinfty%5D&bg=ffffff&fg=545454&s=0&c=20201002) ?)
?)
18 March, 2017 at 6:43 am
Anonymous
It is said at the beginning of section 3 that “much of the theory here extends to the non- -finite setting.”
-finite setting.”
Is the -finite assumption implicitly used somewhere in the proof of Theorem 21? (Or is the theorem true in the non-
-finite assumption implicitly used somewhere in the proof of Theorem 21? (Or is the theorem true in the non- -finite setting?)
-finite setting?)
19 March, 2017 at 6:09 am
Anonymous
In Lemma 9, what norm should one use for the space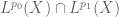 ?
?
In Theorem 21, what norm should one use for the Minkowski sums and
and 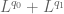 ?
?
22 March, 2017 at 6:05 am
Terence Tao
I don’t believe I using a norm for these spaces anywhere in my text, but the standard norm on the intersection of two normed vector spaces is defined as
of two normed vector spaces is defined as  (one can also use the equivalent norm
(one can also use the equivalent norm 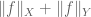 ), and the standard norm on the sum
), and the standard norm on the sum 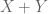 is
is 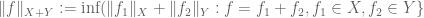 .
.
19 March, 2017 at 10:16 am
Anonymous
In the definition of the distribution function, several other books (e.g. Folland) use instead of
instead of  in the formula
in the formula
In practice of doing analysis (in the case that ), how much difference would this make? For instance, would it affect the proof of Mincinkiewicz interpolation theorem?
), how much difference would this make? For instance, would it affect the proof of Mincinkiewicz interpolation theorem?
6 December, 2017 at 7:10 am
Anonymous
Instead of being right-continuous, one gets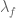 being left-continuous here. That’s the only difference I think. In practice, may be not a big deal.
being left-continuous here. That’s the only difference I think. In practice, may be not a big deal.
6 December, 2017 at 7:08 am
jack
It is said in Wikipedia (https://en.wikipedia.org/wiki/Lorentz_space) that the Lorentz space norm with
with  is the area of the largest rectangle with sides parallel to the coordinate axes that can be inscribed in the graph.
is the area of the largest rectangle with sides parallel to the coordinate axes that can be inscribed in the graph.
However, direct calculation shows that the area of any inscribed rectangle is
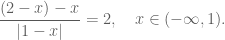
What goes wrong? Can it be explained by Exercise 13?
6 December, 2017 at 7:15 am
Anonymous
The Lorentz norm of an indicator function can be calculated easily. But when it goes to general functions, even just simple functions, the calculation becomes much more difficult. What is this norm really about?
Maybe its property such as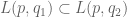 is more important than what it really is?
is more important than what it really is?
6 December, 2017 at 12:33 pm
Terence Tao
Yes, the Lorentz space norm of this function is equal to . As it turns out the dyadic Lorentz space norm is also equal to
. As it turns out the dyadic Lorentz space norm is also equal to  . (In general, the two expressions will be comparable, but not identical.) I find the dyadic norm to be a bit more tractable in computations (for instance it is easy to compute for linear combinations of a few indicator functions, particularly if the sets involved are disjoint and the coefficients are lacunary).
. (In general, the two expressions will be comparable, but not identical.) I find the dyadic norm to be a bit more tractable in computations (for instance it is easy to compute for linear combinations of a few indicator functions, particularly if the sets involved are disjoint and the coefficients are lacunary).
16 December, 2017 at 12:32 pm
Anonymous
In Stein-Weiss, the following inequality is used for the proof of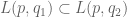 (
( and
and  ):
):
How is this inequality done?
[Upper bound the integral, and then use the monotonicity of norms. -T]
norms. -T]
16 December, 2017 at 7:54 pm
Anonymous
Using the monotonicity of norms, one has
norms, one has
![\displaystyle \left(\sum_{k=-\infty}^{\infty} [f^*(2^{k-1})]^{q_2}2^{kq_2/p}\right)^{q_1/q_2} \leq \sum_{k=-\infty}^{\infty} [f^*(2^{k-1})]^{q_1}2^{kq_1/p}](https://s0.wp.com/latex.php?latex=%5Cdisplaystyle++%5Cleft%28%5Csum_%7Bk%3D-%5Cinfty%7D%5E%7B%5Cinfty%7D+%5Bf%5E%2A%282%5E%7Bk-1%7D%29%5D%5E%7Bq_2%7D2%5E%7Bkq_2%2Fp%7D%5Cright%29%5E%7Bq_1%2Fq_2%7D+%5Cleq+%5Csum_%7Bk%3D-%5Cinfty%7D%5E%7B%5Cinfty%7D+%5Bf%5E%2A%282%5E%7Bk-1%7D%29%5D%5E%7Bq_1%7D2%5E%7Bkq_1%2Fp%7D+&bg=ffffff&fg=545454&s=0&c=20201002)
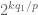 right.
right.
It seems that one cannot get the exponent in
Rewriting the RHS as
![\displaystyle \sum_{k=-\infty}^{\infty} [f^*(2^{k-1})]^{q_1}2^{kq_1/q_2}(2^{kq_1/p-kq_1/q_2})](https://s0.wp.com/latex.php?latex=%5Cdisplaystyle+%5Csum_%7Bk%3D-%5Cinfty%7D%5E%7B%5Cinfty%7D+%5Bf%5E%2A%282%5E%7Bk-1%7D%29%5D%5E%7Bq_1%7D2%5E%7Bkq_1%2Fq_2%7D%282%5E%7Bkq_1%2Fp-kq_1%2Fq_2%7D%29+&bg=ffffff&fg=545454&s=0&c=20201002)
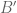 should one use?
should one use?
what
17 December, 2017 at 11:54 am
Anonymous
If in Stein-Weiss,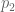 is a typo which should be
is a typo which should be  , then the first inequality here has already given the conclusion.
, then the first inequality here has already given the conclusion.
27 January, 2018 at 7:24 pm
Prove $L^{p_theta }(X)subset L^{p_0}(X)+L^{p_1}(X),$ where $frac{1}{p_theta }:=frac{1-theta }{p_0}+frac{theta }{p_1}.$ | Questions
[…] 245C, Notes 1: Interpolation of L^p spaces […]
16 April, 2020 at 5:23 pm
Anonymous
Dear Professor Tao. I have a question regarding the weak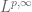 spaces. Assume that
spaces. Assume that  , where the sets
, where the sets  are disjoints, and
are disjoints, and 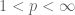 . Is it true that
. Is it true that
with a constant independent of ?
?
Thanks in advance.
16 April, 2020 at 7:12 pm
Terence Tao
No. Consider the case when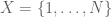 with counting measure and
with counting measure and 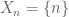 ; then the estimate would be claiming that the
; then the estimate would be claiming that the  norm is controlled by the
norm is controlled by the 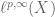 norm uniformly in
norm uniformly in  , which is false.
, which is false.
10 December, 2020 at 12:09 am
Anonymous
In exercise 14,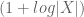 should be
should be 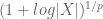 instead? there is a similar problem here:https://math.stackexchange.com/questions/762622/inequality-of-strong-lp-and-weak-lp-norm-on-a-finite-set-with-counting-mea
instead? there is a similar problem here:https://math.stackexchange.com/questions/762622/inequality-of-strong-lp-and-weak-lp-norm-on-a-finite-set-with-counting-mea
[Corrected, thanks – T.]
13 December, 2020 at 5:13 am
Anonymous
Dear Prof.Tao:
How to continuously extend a linear continuous operator on the subspace of $L^\infty$ to $L^\infty$?
Given any subspace $S$ of $L^\infty$, and $T$ is linear continuous operator on $S$ into some Banach space $B$, is there any general method to extend from $S$ to $L^\infty$ in linear continuous manner?
In this post, it is said that we can maybe non-uniquely extend from the space of simple measurable with finite measure support to $L^\infty$ in a linear continuous manner, how to do this, any hint? I am stuck in this problem, thanks in advance.
13 December, 2020 at 10:32 am
Terence Tao
Both existence and uniqueness are problematic in general. If one of the spaces involves a finite measure then it becomes a complete Banach lattice and the usual proof of Hahn-Banach goes through to give existence of an extension, and sigma-finite measures might still be OK, but I think general measures are not. (There is a theorem of Kelley that says that a Hahn-Banach type extension theorem for a Banach space target
spaces involves a finite measure then it becomes a complete Banach lattice and the usual proof of Hahn-Banach goes through to give existence of an extension, and sigma-finite measures might still be OK, but I think general measures are not. (There is a theorem of Kelley that says that a Hahn-Banach type extension theorem for a Banach space target  is possible if and only if
is possible if and only if  is isomorphic to the space of continuous functions on a Stonean space, which when applied to
is isomorphic to the space of continuous functions on a Stonean space, which when applied to  using Gelfand duality I think comes down to requiring the underlying measure algebra to be complete, which is true when the measure is finite or sigma-finite but I believe there are counterexamples in general.)
using Gelfand duality I think comes down to requiring the underlying measure algebra to be complete, which is true when the measure is finite or sigma-finite but I believe there are counterexamples in general.)
13 December, 2020 at 5:59 pm
Anonymous
Is it possible to extend the interpolation theorem with restricted weak-type bounds for operators defined on mixed L^p(L^q) spaces?
13 December, 2020 at 8:32 pm
Terence Tao
Partially, but the more detailed answer is rather complicated; see for instance this paper of Fernandez.
21 July, 2021 at 3:30 am
Gerd Wachsmuth
In Exercise 34, I think one needs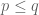 for the estimate of
for the estimate of  , see also https://mathoverflow.net/questions/336970/the-norm-of-tensor-product-operator-on-lp-spaces.
, see also https://mathoverflow.net/questions/336970/the-norm-of-tensor-product-operator-on-lp-spaces.
Otherwise, it would be possible to deduce the Riesz-Thorin interpolation theorem in the real case with constant $1$ only under the requirement $p_\theta \le q_\theta$ via Marcinkiewicz (or without any requirement via the complex Riesz-Thorin theorem). This, however, is not true, see, e.g., https://link.springer.com/article/10.1007/s000130050241.
[Corrected, thanks – T.]
7 June, 2022 at 11:30 pm
Anonymous
Dear Prof. Tao,
Is it possible to prove the continuous embeddings of L^\infty(L^2)\capL^2(H^1) in L^{4,1}(H^{1/2}) ?
11 June, 2022 at 3:32 pm
Terence Tao
No, there is no such embedding. Consider a function of the form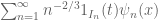 , where
, where  is a function of frequency
is a function of frequency 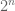 normalised in
normalised in 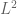 (so that its
(so that its  norm is like
norm is like 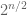 and its
and its 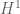 norm is like
norm is like 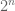 ) and the
) and the 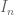 are disjoint time intervals of length
are disjoint time intervals of length  . Then one can check that this function is bounded in
. Then one can check that this function is bounded in 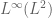 and
and 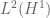 but not
but not 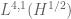 . (More generally, one should experiment with various combinations of rescaled and translated bump functions in order to gain intuition as to whether a given interpolation inequality might be true.)
. (More generally, one should experiment with various combinations of rescaled and translated bump functions in order to gain intuition as to whether a given interpolation inequality might be true.)
8 July, 2022 at 2:59 am
Anonymous
Dear prof. Tao,
I read the Riesz Thorin interpolation for vector valued.(For explanation, if i want to get l2 sum of Lp norm, Enough to check sup of L2 and l1 sum of Lq norm) But, Vector valued version RT interpolation that I read has the assumption that the operator T is a linear operator. In the proof, Linearity is needed, when proceeding approximation argument. is it possible to use Vector valued Risez thorin Interpolation theorem for sublinear case?(not marcinkiewicz interpolation for vector valued. It does not interpolate the norm of valued) Would you recommend the refer for this sub linear version of proof?
12 July, 2022 at 2:31 pm
Anonymous
No. Riesz Thorin interpolation only works for linear operators, while Marcinkiewicz interpolation also works for sublinear operators.
12 July, 2022 at 4:58 pm
Anonymous
Thanks for replying!
In page 464 of Harmonic Analysis: Real-Variable Methods, Orthogonality, and Oscillatory Integrals by Stein, I read the middle part of this page using interpolation for sublinear operator. Would you please tell me the interpolation statement they use?
At first, I think, this is the interpolation which is in page 399 problem 5.5.2 of Classical Fourier Analysis by L.Grafakos.
But in here, we need the linearity assumption. You may recommend a reference paper or book for this interpolation.
22 July, 2022 at 4:48 pm
Anonymous
Stein’s book refers to Lorentz spaces interpolation of mixed norms. Dr. Tao mentioned a paper by Fernandez in one of the comments, and the URL is:
Click to access 81999059.pdf
22 July, 2022 at 4:51 pm
Anonymous
Proposition 9.1 on page 143.