Suppose one is given a -tuple
of
distinct integers for some
, arranged in increasing order. When is it possible to find infinitely many translates
of
which consists entirely of primes? The case
is just Euclid’s theorem on the infinitude of primes, but the case
is already open in general, with the
case being the notorious twin prime conjecture.
On the other hand, there are some tuples for which one can easily answer the above question in the negative. For instance, the only translate of
that consists entirely of primes is
, basically because each translate of
must contain an even number, and the only even prime is
. More generally, if there is a prime
such that
meets each of the
residue classes
, then every translate of
contains at least one multiple of
; since
is the only multiple of
that is prime, this shows that there are only finitely many translates of
that consist entirely of primes.
To avoid this obstruction, let us call a -tuple
admissible if it avoids at least one residue class
for each prime
. It is easy to check for admissibility in practice, since a
-tuple is automatically admissible in every prime
larger than
, so one only needs to check a finite number of primes in order to decide on the admissibility of a given tuple. For instance,
or
are admissible, but
is not (because it covers all the residue classes modulo
). We then have the famous Hardy-Littlewood prime tuples conjecture:
Conjecture 1 (Prime tuples conjecture, qualitative form) If
is an admissible
-tuple, then there exists infinitely many translates of
that consist entirely of primes.
This conjecture is extremely difficult (containing the twin prime conjecture, for instance, as a special case), and in fact there is no explicitly known example of an admissible -tuple with
for which we can verify this conjecture (although, thanks to the recent work of Zhang, we know that
satisfies the conclusion of the prime tuples conjecture for some
, even if we can’t yet say what the precise value of
is).
Actually, Hardy and Littlewood conjectured a more precise version of Conjecture 1. Given an admissible -tuple
, and for each prime
, let
denote the number of residue classes modulo
that
meets; thus we have
for all
by admissibility, and also
for all
. We then define the singular series
associated to
by the formula
where is the set of primes; by the previous discussion we see that the infinite product in
converges to a finite non-zero number.
We will also need some asymptotic notation (in the spirit of “cheap nonstandard analysis“). We will need a parameter that one should think of going to infinity. Some mathematical objects (such as
and
) will be independent of
and referred to as fixed; but unless otherwise specified we allow all mathematical objects under consideration to depend on
. If
and
are two such quantities, we say that
if one has
for some fixed
, and
if one has
for some function
of
(and of any fixed parameters present) that goes to zero as
(for each choice of fixed parameters).
Conjecture 2 (Prime tuples conjecture, quantitative form) Let
be a fixed natural number, and let
be a fixed admissible
-tuple. Then the number of natural numbers
such that
consists entirely of primes is
.
Thus, for instance, if Conjecture 2 holds, then the number of twin primes less than should equal
, where
is the twin prime constant
As this conjecture is stronger than Conjecture 1, it is of course open. However there are a number of partial results on this conjecture. For instance, this conjecture is known to be true if one introduces some additional averaging in ; see for instance this previous post. From the methods of sieve theory, one can obtain an upper bound of
for the number of
with
all prime, where
depends only on
. Sieve theory can also give analogues of Conjecture 2 if the primes are replaced by a suitable notion of almost prime (or more precisely, by a weight function concentrated on almost primes).
Another type of partial result towards Conjectures 1, 2 come from the results of Goldston-Pintz-Yildirim, Motohashi-Pintz, and of Zhang. Following the notation of this recent paper of Pintz, for each , let
denote the following assertion (DHL stands for “Dickson-Hardy-Littlewood”):
Conjecture 3 (
) Let
be a fixed admissible
-tuple. Then there are infinitely many translates
of
which contain at least two primes.
This conjecture gets harder as gets smaller. Note for instance that
would imply all the
cases of Conjecture 1, including the twin prime conjecture. More generally, if one knew
for some
, then one would immediately conclude that there are an infinite number of pairs of consecutive primes of separation at most
, where
is the minimal diameter
amongst all admissible
-tuples
. Values of
for small
can be found at this link (with
denoted
in that page). For large
, the best upper bounds on
have been found by using admissible
-tuples
of the form
where denotes the
prime and
is a parameter to be optimised over (in practice it is an order of magnitude or two smaller than
); see this blog post for details. The upshot is that one can bound
for large
by a quantity slightly smaller than
(and the large sieve inequality shows that this is sharp up to a factor of two, see e.g. this previous post for more discussion).
In a key breakthrough, Goldston, Pintz, and Yildirim were able to establish the following conditional result a few years ago:
Theorem 4 (Goldston-Pintz-Yildirim) Suppose that the Elliott-Halberstam conjecture
is true for some
. Then
is true for some finite
. In particular, this establishes an infinite number of pairs of consecutive primes of separation
.
The dependence of constants between and
given by the Goldston-Pintz-Yildirim argument is basically of the form
. (UPDATE: as recently observed by Farkas, Pintz, and Revesz, this relationship can be improved to
.)
Unfortunately, the Elliott-Halberstam conjecture (which we will state properly below) is only known for , an important result known as the Bombieri-Vinogradov theorem. If one uses the Bombieri-Vinogradov theorem instead of the Elliott-Halberstam conjecture, Goldston, Pintz, and Yildirim were still able to show the highly non-trivial result that there were infinitely many pairs
of consecutive primes with
(actually they showed more than this; see e.g. this survey of Soundararajan for details).
Actually, the full strength of the Elliott-Halberstam conjecture is not needed for these results. There is a technical specialisation of the Elliott-Halberstam conjecture which does not presently have a commonly accepted name; I will call it the Motohashi-Pintz-Zhang conjecture in this post, where
is a parameter. We will define this conjecture more precisely later, but let us remark for now that
is a consequence of
.
We then have the following two theorems. Firstly, we have the following strengthening of Theorem 4:
Theorem 5 (Motohashi-Pintz-Zhang) Suppose that
is true for some
. Then
is true for some
.
A version of this result (with a slightly different formulation of ) appears in this paper of Motohashi and Pintz, and in the paper of Zhang, Theorem 5 is proven for the concrete values
and
. We will supply a self-contained proof of Theorem 5 below the fold, the constants upon those in Zhang’s paper (in particular, for
, we can take
as low as
, with further improvements on the way). As with Theorem 4, we have an inverse quadratic relationship
.
In his paper, Zhang obtained for the first time an unconditional advance on :
This is a deep result, building upon the work of Fouvry-Iwaniec, Friedlander-Iwaniec and Bombieri–Friedlander–Iwaniec which established results of a similar nature to but simpler in some key respects. We will not discuss this result further here, except to say that they rely on the (higher-dimensional case of the) Weil conjectures, which were famously proven by Deligne using methods from l-adic cohomology. Also, it was believed among at least some experts that the methods of Bombieri, Fouvry, Friedlander, and Iwaniec were not quite strong enough to obtain results of the form
, making Theorem 6 a particularly impressive achievement.
Combining Theorem 6 with Theorem 5 we obtain for some finite
; Zhang obtains this for
but as detailed below, this can be lowered to
. This in turn gives infinitely many pairs of consecutive primes of separation at most
. Zhang gives a simple argument that bounds
by
, giving his famous result that there are infinitely many pairs of primes of separation at most
; by being a bit more careful (as discussed in this post) one can lower the upper bound on
to
, and if one instead uses the newer value
for
one can instead use the bound
. (Many thanks to Scott Morrison for these numerics.) UPDATE: These values are now obsolete; see this web page for the latest bounds.
In this post we would like to give a self-contained proof of both Theorem 4 and Theorem 5, which are both sieve-theoretic results that are mainly elementary in nature. (But, as stated earlier, we will not discuss the deepest new result in Zhang’s paper, namely Theorem 6.) Our presentation will deviate a little bit from the traditional sieve-theoretic approach in a few places. Firstly, there is a portion of the argument that is traditionally handled using contour integration and properties of the Riemann zeta function; we will present a “cheaper” approach (which Ben Green and I used in our papers, e.g. in this one) using Fourier analysis, with the only property used about the zeta function being the elementary fact that blows up like
as one approaches
from the right. To deal with the contribution of small primes (which is the source of the singular series
), it will be convenient to use the “
-trick” (introduced in this paper of mine with Ben), passing to a single residue class mod
(where
is the product of all the small primes) to end up in a situation in which all small primes have been “turned off” which leads to better pseudorandomness properties (for instance, once one eliminates all multiples of small primes, almost all pairs of remaining numbers will be coprime).
— 1. The -trick —
In this section we introduce the “-trick”, which is a simple but useful device that automatically takes care of local factors arising from small primes, such as the singular series
. The price one pays for this trick is that the explicit decay rates in various
terms can be rather poor, but for the applications here, we will not need to know any information on these decay rates and so the
-trick may be freely applied.
Let be a natural number, which should be thought of as either fixed and large, or as a very slowly growing function of
. Actually, the two viewpoints are basically equivalent for the purposes of asymptotic analysis (at least at the qualitative level of
decay rates), thanks to the following basic principle:
Lemma 7 (Overspill principle) Let
be a quantity depending on
and
. Then the following are equivalent:
- (i) For every fixed
there exists a fixed
such that
for all fixed
.
- (ii) We have
whenever
is a function of
going to infinity that is sufficiently slowly growing. (In other words, there exists a function
going to infinity with the property that
whenever
is a natural number-valued function of
is such that
as
and
for all sufficiently large
.)
This principle is closely related to the overspill principle from nonstandard analysis, though we will not explicitly adopt a nonstandard perspective here. It is also similar in spirit to the diagonalisation trick used to prove the Arzela-Ascoli theorem.
Proof: We first show that (i) implies (ii). By (i), we see that for every natural number , we can find a real number
with the property that
whenever ,
, and
are such that
. By increasing the
as necessary we may assume that they are increasing and go to infinity as
. If we then define
to equal the largest natural number
for which
, or equal to
if no such number exists, then one easily verifies that
whenever
goes to infinity and is bounded by
for sufficiently large
.
Now we show that (ii) implies (i). Suppose for contradiction that (i) failed, then we can find a fixed with the property that for any natural number
, there exist
such that
for arbitrarily large
. We can select the
to be increasing to infinity, and then we can find a sequence
increasing to infinity such that
for all
; by increasing
as necessary, we can also ensure that
for all
and
. If we then define
to be
when
, and
for
, we see that
whenever
, contradicting (ii).
Henceforth we will usually think of as a sufficiently slowly growing function of
, although we will on occasion take advantage of Lemma 7 to switch to thinking of
as a large fixed quantity instead. In either case, we should think of
as exceeding the size of fixed quantities such as
or
, at least in the limit where
is large; in particular, for a fixed
-tuple
, we will have
if is large enough. A particular consequence of the growing nature of
is that
as this follows from the absolutely convergent nature of the sum and hence also
. As a consequence of this, once we “turn off” all the primes less than
, any errors in our sieve-theoretic analysis which are quadratic or higher in
can be essentially ignored, which will be very convenient for us. In a similar vein, for any fixed
-tuple
, one has
which allows one to truncate the singular series:
In order to “turn off” all the small primes, we introduce the quantity , defined as the product of all the primes up to
(i.e. the primorial of
):
As is going to infinity,
is going to infinity also (but as slowly as we please). The idea of the
-trick is to search for prime patterns in a single residue class
, which as mentioned earlier will “turn off” all the primes less than
in the sieve-theoretic analysis.
Using (4) and the Chinese remainder theorem, we may thus approximate the singular series as
where is the Euler totient function of
, and
is the set of residue classes
such that all of the shifts
are coprime to
. Note that if
consists purely of primes and
is sufficiently large, then
must lie in one of the residue classes in
. Thus we can count tuples with
all prime by working in each residue class in
separately. We conclude that Conjecture 2 is equivalent to the following “
-tricked version” in which the singular series is no longer present (or, more precisely, has been replaced by some natural normalisation factors depending on
, such as
):
Conjecture 8 (Prime tuples conjecture, W-tricked quantitative form) Let
be a fixed natural number, and let
be a fixed admissible
-tuple. Assume
is a sufficiently slowly growing function of
. Then for any residue class
in
, the number of natural numbers
with
such that
consists entirely of primes is
.
We will work with similarly -tricked asymptotics in the analysis below.
— 2. Sums of multiplicative functions —
As a result of the sieve-theoretic computations to follow, we will frequently need to estimate sums of the form
and
where is a multiplicative function, the sieve level
(also denoted
in some literature) is a fixed power of
(such as
or
),
is the Möbius function,
is a fixed smooth compactly supported function,
is a (possibly half-infinite) interval in
, and
is the set of square-free numbers that are products
of distinct primes
in
. (Actually, in applications
won’t quite be smooth, but instead have some high order of differentiability (e.g.
times continuously differentiable for some
), but we can extend the analysis of smooth
to sufficiently differentiable
by various standard limiting or approximation arguments which we will not dwell on here.) We will also need to control the more complicated variant
where are also smooth compactly supported functions. In practice, the interval
will be something like
,
,
. In particular, thanks to the
-trick we will be able to turn off all the primes up to
, so that
only contains primes larger than
, allowing us to take advantage of bounds such as (2).
Once is restricted to
, the quantity
is determined entirely by the values of the multiplicative function
at primes in
:
In applications, will have the size bound
for all and some fixed positive
(note that we allow the implied constants in the
notation to depend on quantities such as
); we refer to
as the dimension of the multiplicative function
. Henceforth we assume that
has a fixed dimension
. We remark that we could unify the treatment of
and
in what follows by allowing multiplicative functions of negative dimension, but we will avoid doing so here. In our applications
will be an integer; one could also generalise much of the discussion below to the fractional dimension case, but we will not need to do so here.
Traditionally the above expressions are handled by complex analysis, starting with Perron’s formula. We will instead take a slightly different Fourier-analytic approach. We perform a Fourier expansion of the smooth compactly supported function to obtain a representation
for some Schwartz function ; in particular,
is rapidly decreasing. (Strictly speaking,
is the Fourier transform of
shifted in the complex domain by
, rather than the true Fourier transform of
, but we will ignore this distinction for the purposes of this discussion.) In particular we have
for any . By Fubini’s theorem, we can thus write
as
which factorises as
Similarly one has
and
In order to use asymptotics of the Riemann zeta function near the pole , it is convenient to temporarily truncate the above integrals to the region
or
:
Lemma 9 For any fixed
, we have
and
and
Also we have the crude bound
Proof: We begin with the bounds on . From (6) we have
for (which forces
, so there is no issue with the singularity of the logarithm) and thus
Since
we see on taking logarithms that
and thus
The bounds on then follow from the rapid decrease of
. The bounds for
and
are proven similarly.
From (6) and the restriction of to quantities larger than
, we see that
and
and
where is the restricted Euler product
which is well-defined for at least (and this is the only region of
for which we will need
).
We now specialise to the model case , in which case
where is the Riemann zeta function. Using the basic (and easily proven) asymptotic
for
near
for , if
is sufficiently slowly growing (this can be seen by first working with a fixed large
and then using Lemma 7). Note that because of the above truncation, we do not need any deeper bounds on
than what one can obtain from the simple pole at
; in particular no zero-free regions near the line
are needed here. (This is ultimately because of the smooth nature of
, which is sufficient for the applications in this post; if one wanted rougher cutoff functions here then the situation is closer to that of the prime number theorem, and non-trivial zero-free regions would be required.)
We conclude in the case that
and
and
using the rapid decrease of , we thus have
and
and
We can rewrite these expressions in terms of instead of
. Using the Gamma function identity
and (7) we see that
whilst from differentiating (7) times at the origin (after first dividing by
) we see that
Combining these two methods, we also see that
We have thus obtained the following asymptotics:
Proposition 10 (Asymptotics without prime truncation) Suppose that
, and that
has dimension
for some fixed natural number
. Then we have
and
and
These asymptotics will suffice for the treatment of the Goldston-Pintz-Yildirim theorem (Theorem 4). For the Motohashi-Pintz-Zhang theorem (Theorem 5) we will also need to deal with truncated intervals , such as
; we will discuss how to deal with these truncations later.
— 3. The Goldston-Yildirim-Pintz theorem —
We are now ready to state and prove the Goldston-Yildirim-Pintz theorem. We first need to state the Elliott-Halberstam conjecture properly.
Let be the von Mangoldt function, thus
equals
when
is equal to a prime
or a power of that prime, and equal to zero otherwise. The prime number theorem in arithmetic progressions tells us that
for any fixed arithmetic progression with
coprime to
. In particular,
where are the residue classes mod
that are coprime to
. By invoking the Siegel-Walfisz theorem one can obtain the improvement
for any fixed (though, annoyingly, the implied constant here is only ineffectively bounded with current methods; see this previous post for further discussion).
The above error term is only useful when is fixed (or is of logarithmic size in
). For larger values of
, it is very difficult to get good error terms for each
separately, unless one assumes powerful hypotheses such as the generalised Riemann hypothesis. However, it is possible to obtain good control on the error term if one averages in
. More precisely, for any
, let
denote the following assertion:
Conjecture 11 (
) One has
for all fixed
.
This should be compared with the asymptotic for some absolute constant
, as can be deduced for instance from Proposition 10. The Elliott-Halberstam conjecture is the assertion that
holds for all
. This remains open, but the important Bombieri-Vinogradov theorem establishes
for all
. Remarkably, the threshold
is also the limit of what one can establish if one directly invokes the generalised Riemann hypothesis, so the Bombieri-Vinogradov theorem is often referred to as an assertion that the generalised Riemann hypothesis (or at least the Siegel-Walfisz theorem) holds “on the average”, which is often good enough for sieve-theoretic purposes.
We may replace the von Mangoldt function with the slight variant
, defined to equal
when
is a prime
and zero otherwise. Using this replacement, as well as the prime number theorem (with
error term), it is not difficult to show that
is equivalent to the estimate
Now we establish Theorem 4. Suppose that holds for some fixed
, let
be sufficiently large depending on
but otherwise fixed, and let
be a fixed admissible
-tuple. We would like to show that there are infinitely many
such that
contains at least two primes. We will begin with the
-trick, restricting
to a residue class
with
(note that
is non-empty because
is admissible).
The general strategy will be as follows. We will introduce a weight function that obeys the upper bound
for all and some fixed
, where
is a fixed power of
(we will eventually take
). (The factors of
,
, and
on the right-hand side are natural normalisations coming from sieve theory and the reader should not pay too much attention to them.) Informally, (9) says that
has some normalised density at most
, and then (10) roughly speaking asserts that relative to the weight
,
has a probability of at least
of being prime. If we sum (10) for all
and then subtract off
copies of (9), we conclude that
In particular, if we have the crucial inequality
and so is positive for at least one value of
between
and
. This can only occur if
contains two or more primes. Thus we must have
containing at least two primes for some
between
and
; sending
off to infinity then gives
as desired.
It thus suffices to find a weight function obeying the required properties (9), (10) with parameters
obeying the key inequality (11). It is thus of interest to make
as large a power of
as possible, and to minimise the ratio between
and
. It is in the former task that the Elliott-Halberstam hypothesis will be crucial.
The key is to find a good choice of , and the selection of this weight is arguably the main contribution of Goldston, Pintz, and Yildirim, who use a carefully modified version of the Selberg sieve. Following (a slight modification of) the Goldston-Pintz-Yildirim argument, we will take a weight of the form
, where
where is a fixed smooth non-negative function supported on
to be chosen later,
, and
is the polynomial
The intuition here is that is a truncated approximation to a function of the form
for some natural number , which one can check is only non-vanishing when
has at most
distinct prime factors in
. So
is concentrated on those numbers
for which
already has few prime factors for
, which will assist in making the ratio
as small as possible.
Clearly is non-negative. Now we consider the task of estimating the left-hand side of (9). Expanding out
using (12) and interchanging summations, we can expand this expression as
The constraint is equivalent to requiring that for each prime
dividing
,
lies in one of the residue classes
for
. By choice of
,
, so all the
are distinct, and so we are constraining
to lie in one of
residue classes modulo
for each
; together with the constraint
and the Chinese remainder theorem, we are thus constraining
to
residue classes modulo
, where
is the number of prime factors of
. We thus have
Note from the support of that
may be constrained to be at most
, so that
is at most
. We can thus express the left-hand side of (9) as the main term
plus an error
By Proposition 10, the error term is . So if we set
then the error term will certainly give a negligible contribution to (9) with plenty of room to spare. (But when we come to the more difficult sum (10), we will have much less room – only a superlogarithmic amount of room, in fact.) To show (9), it thus suffices to show that
But by Proposition 10 (applied to the -dimensional multiplicative function
) and the support of
, this bound holds with
equal to the quantity
Now we turn to (10). Fix . Repeating the arguments for (9), we may expand the left-hand side of (10) as
Now we consider the inner sum
As discussed earlier, the conditions and
split into
residue classes
. However, if
for one of the primes
dividing
, then
must vanish (since
is much less than
). So there are actually only
residue classes
for which
is coprime to
. We thus have
Remark 1 There is an inefficiency here; the supremum in (13) is over all primitive residue classes
, but actually one only needs to take the supremum over the
residue classes
for which
, where
. This inefficiency is not exploitable if we insist on using the Elliott-Halberstam conjecture as the starting hypothesis, but will be used in the arguments of the next section in which a more lightweight hypothesis is utilised.
The left-hand side of (10) is thus equal to the main term
plus an error term
We first deal with the error term. Since is in
and is bounded by
on the support of this function, and each
has
representations of the form
, we can bound this expression by
Note that we are assuming to be a fixed smooth compactly supported function and so it has magnitude
. On the other hand, from Proposition 10 and the trivial bound
we have
while from (8) (and here we crucially use the choice of
) one easily verifies that
for any fixed . By the Cauchy-Schwarz inequality we see that the error term to (10) is negligible (assuming
sufficiently slowly growing of course). Meanwhile, the main term can be rewritten as
where is the
-dimensional multiplicative function
Applying Proposition 10, we obtain (10) with
To obtain the crucial inequality (11), we thus need to locate a fixed smooth non-negative function supported on obeying the inequality
In principle one can use calculus of variations to optimise the choice of here (it will be the ground state of a certain one-dimensional Schrödinger operator), but one can already get a fairly good result here by a specific choice of
that is amenable for computations, namely a polynomial of the form
for
and some integer
, with
vanishing for
and smoothly truncated to
somehow at negative values of
. Strictly speaking, this
is not admissible here because it is not infinitely smooth at
, being only
times continuously differentiable instead, but one can regularise this function to be smooth without significantly affecting either side of (14), so we will go ahead and test (14) with this function and leave the regularisation details to the reader. The inequality then becomes (after cancelling some factors)
Using the Beta function identity
and the preceding equation now becomes
which simplifies to
Actually, the same inequality is also applicable when is real instead of integer, using Gamma functions in place of factorials; we leave the details to the interested reader. We can then optimise in
by setting
, arriving at the inequality
But as long as , this inequality is satisfiable for any
larger than
. This concludes the proof of Theorem 4.
Remark 2 One can obtain slightly better dependencies of
in terms of
by using more general functions for
than the monomials
, for instance one can take linear combinations of such functions. See the paper of Goldston, Pintz, and Yildirim for details. Unfortunately, as noted in this survey of Soundararajan, one has the general inequality
which defeats any attempt to directly use this method using only the Bombieri-Vinogradov result that
holds for all
. We show (17) in the case when
is large. Write
, then (17) simplifies to
The right-hand side simplifies after some integration by parts to
Subtracting off
from both sides, one is left with
From the fundamental theorem of calculus and Cauchy-Schwarz, one has the bound
Using this bound for
close to
and dominating
by
for
far from
, we obtain the claim (at least if
is large enough). There is some slack in this argument; it would be of interest to calculate exactly what the best constants are in (17), so that one can obtain the optimal relationship between
and
.
To get around this obstruction (17) in the unconditional setting when one only has
for
, Goldston, Pintz, and Yildirim also considered sums of the form
in which
was now outside (but close to)
. While the bounds here were significantly inferior to those in (10), they were still sufficient to prove a variant of the inequality (11) to get reasonably small gaps between primes.
— 4. The Motohashi-Pintz-Zhang theorem —
We now modify the above argument to give Theorem 5. Our treatment here is different from that of Zhang in that it employs the method of Buchstab iteration; a related argument also appears in the paper of Motohashi and Pintz. This arrangement of the argument leads to a more efficient dependence of on
than in the paper of Zhang. (The argument of Motohashi and Pintz is a bit more complicated and uses a slightly different formulation of the base conjecture
, but the final bounds are similar to those given here, albeit with non-explicit constants in the
notation.)
The main idea here is to truncate the interval of relevant primes from
to
for some small
. Somewhat remarkably, it turns out that this apparently severe truncation does not affect the sums (9), (10) here as long as
is large (which is going to be the case in practice, with
being comparable to
). The intuition is that
was already concentrated on those
for which
had about
factors, and it is too “expensive” for one of these factors to as large as
or more, as it forces many of the other factors to be smaller than they “want” to be. The advantage of truncating the set of primes this way is that the version of the Elliott-Halberstam conjecture needed also acquires the same truncation, which gives that version a certain “well-factored” form (in the spirit of the work of Bombieri, Fouvry, Friedlander, and Iwaniec) which is essential in being able to establish that conjecture unconditionally for some suitably small
.
To make this more precise, we first formalise the conjecture for
mentioned earlier.
Conjecture 12 (
) Let
be a fixed
-tuple (not necessarily admissible) for some fixed
, and let
be a primitive residue class. Then
for any fixed
, where
and
is the quantity
and
This is the -tricked formulation of the conjecture as (implicitly) stated in Zhang’s paper, which did not have the restriction
present (and with the interval
enlarged from
to
, and
was required to be admissible). However the two formulations are morally equivalent (and Zhang’s arguments establish Theorem 6 with
as stated). From the prime number theorem in arithmetic progressions (with
error term) together with Proposition 10 we observe that we may replace (18) here by the slight variant
without affecting the truth of .
It is also not difficult to deduce from
after using a Cauchy-Schwarz argument to dispose of the
residue classes
in the above sum (cf. the treatment of the error term in (10) in the previous section); we leave the details to the interested reader. Note however that whilst
demands control over all primitive residue classes
in a given modulus
, the conjecture
only requires control of a much smaller number of residue classes (roughly polylogarithmic in number, on average). Thus
is simpler than
, though it is still far from trivial.
We now begin the proof of Theorem 5. Let be such that
holds, and let
be a sufficiently large quantity depending on
but which is otherwise fixed. As before, it suffices to locate a non-negative sieve weight
that obeys the estimates (9), (10) for parameters
that obey the key inequality (11), and with
smooth and supported on
. The choice of weight
is almost the same as before; it is also given as a square
with
given by (12), but now the interval
is truncated to
instead of
. Also, in this argument we take
We now establish (9). By repeating the previous arguments, the left-hand side of (9) is equal to a main term
plus an error term which continues to be acceptable (indeed, the error term is slightly smaller than in the previous case due to the truncated nature of ). At this point in the previous section we applied Proposition 10, but that proposition was only available for the untruncated interval
instead of the truncated interval
. One could try to adapt the proof of that proposition to the truncated case, but then one is faced with the problem of controlling the truncated zeta function
. While one can eventually get some reasonable asymptotics for this function, it seems to be more efficient to eschew Fourier analysis and work entirely in “physical space” by the following partial Möbius inversion argument. Write
, thus
. Observe that for any
, the quantity
equals
when
lies in
and vanishes otherwise. Hence, for any function
of
and
supported on squarefree numbers we have the partial Mobius inversion formula
and so the main term (20) can be expressed as
We first dispose of the contribution to (21) when share a common prime factor
for some
. For any fixed
, we can bound this contribution by
Factorising the inner two sums as an Euler product, this becomes
[UPDATE: The above argument is not quite correct; a corrected (and improved) version is given at this newer post.] The product is by e.g. Mertens’ theorem, while
. So the contribution of this case is negligible.
If do not share a common factor
for any
, then we can factor
as
. Rearranging this portion of (21) and then reinserting the case when
have a common factor
for some
, we may write (21) up to negligible errors as
Note that we can restrict to be at most
as otherwise the
factors vanish. The inner sum
is now of the form that can be treated by Proposition 10, and takes the form
Here we make the technical remark that the translates of by shifts between
and
are uniformly controlled in smooth norms, which means that the
error here is uniform in the choices of
.
Let us first deal with the contribution of the error term. This is bounded by
The inner sum factorises as
which by Mertens’ theorem is (albeit with a rather large implied constant!), so this error is negligible for the purposes of (9). Indeed, (9) is now reduced to the inequality
Note that the factor increases very rapidly with
when
is large, which basically means that any non-trivial shift of the
factors to the left by
or
will cause the integral in (22) to decrease dramatically. Since all the
in
are either equal to
or bounded below by
, this will cause the
term to dominate in the regime when
is large (or more precisely
), which is the case in applications.
At this point, in order to perform the computations cleanly, we will mimic the arguments from the previous section and take the explicit choice
for some integer and
(and some smooth continuation to
for negative
, and so
for positive . (Again, this function is not quite smooth at
, but this issue can be dealt with by an infinitesimal regularisation argument which we omit here.) The left-hand side of (22) now becomes
The integral here is a little bit more complicated than a beta integral. To estimate it, we use the beta function identity to observe that
and
and hence by Cauchy-Schwarz
This Cauchy-Schwarz step is a bit wasteful when are far apart, but this does seems to only lead to a minor loss of efficiency in the estimates. We have thus bounded the left-hand side of (22) by
It is now convenient to collapse the double summation to a single summation. We may bound
(since is less than the greater of
and
) and observe that each
has
representations of the form
, so we may now bound the left-hand side of (22) by
Note that an element of
is either equal to
, or lies in the interval
for some natural number
. In the latter case, we have
In particular, this expression vanishes if . We can thus bound the left-hand side of (22) by
then we have thus bounded the left-hand side of (22) by
when , while in general we have the Buchstab identity
as can be seen by isolating the smallest prime in all the terms in (23) with
. (This inequality is very close to being an identity, the only loss coming from the possibility of the prime factor
being repeated in a term associated to
.) We can iterate this identity to obtain the following conclusion:
whenever
and
for some fixed
, with the error term being uniform in the choice of
.
Proof: Write . We prove the bound
by strong induction on
. The case
follows from (24). Now suppose that
and that the claim has already been proven for smaller
. Let
and
. Note that
whenever
. We thus have from (25) and the induction hypothesis that
applying Mertens’ theorem (or the prime number theorem) we have
and the claim follows from the telescoping identity
Applying this inequality, we have established (22) with
We remark that as a first approximation we have
and
so in the regime ,
is roughly
, which will be negligible for the parameter ranges of
of interest. Thus the
in this argument is quite close to the
from (15) in practice.
Now we turn to (10). Fix . As in the previous section, we can bound the left-hand side of (10) as the sum of the main term
plus an error term
where is the quantity
is the polynomial
, and
was defined in (19). Using the hypothesis
and Cauchy-Schwarz as in the previous section we see that the error term is negligible for the purposes of establishing (10). As for the main term, the same argument used to reduce (9) to (22) shows that (10) reduces to
Here, we can do something a bit crude; with our choice of , the integrand is non-negative, so we can simply discard all but the
term and reduce to
(The intuition here is that by refusing to sieve using primes larger than , we have enlarged the sieve
, which makes the upper bound (9) more difficult but the lower bound (10) actually becomes easier.) So we can take the same choice (16) of
as in the previous section:
Inserting this and (26) into (11) and simplifying, we see that we can obtain once we can verify the inequality
As before, can be taken to be non-integer if desired. Setting
to be slightly larger than
we obtain Theorem 5.
— 5. Using optimal values of (NEW, June 5, 2013) —
We can do better than given above by using an optimal value of . The following result was obtained recently by Farkas, Pintz, and Revesz, and independently worked out by commenters on this blog:
Theorem 14 (Optimal GPY weight) Let
be an integer. Then the ratio
where
is a smooth function with
that is not identically vanishing, has a minimal value of
where
is the first zero of the Bessel function
. Furthermore, this minimum is attained if (and only if)
is a scalar multiple of the function
Proof: The function , by definition, obeys the Bessel differential equation
and also vanishes to order at the origin. From this and routine computations it is easy to see that
is smooth, strictly positive on
, and obeys the differential equation
If we write , which is well-defined away from
since
is non-vanishing on
, then
obeys the Ricatti-type equation
Now consider the quadratic form
for smooth functions with
. A calculation using (29) and integration by parts shows that
and so , giving the first claim; the second claim follows by noting that
vanishes if and only if
is a scalar multiple of
. (Note that the integration by parts is a little subtle, because
vanishes to first order at
and so
blows up to first order; but
still vanishes to first order at
, allowing one to justify the integration by parts by a standard limiting argument.)
If we now test (14) with a function which is smooth, vanishes to order
at
, and has a
derivative equal to
, we see that we can deduce
from
whenever
Using the known asymptotic
for and large
(see e.g. Abramowitz and Stegun), this is asymptotically of the form
or
thus giving a relationship of the form that is superior to the previous relationship
.
A similar argument can be given for Theorem 5, using of the form above rather than a monomial
(and extended by zero to
). For future optimisation we consider a generalisation
of
in which the interval
is of the form
rather than
, so that
is now
rather than
. As before, the key point is the estimation of
. The arguments leading to (22) go through for any test function
, so we have to show
As has
derivative equal to
, this is
We need some sign information on :
Lemma 15 On
,
is positive,
is negative and
is positive.
Proof: From (28) we have
From construction we already know that is positive on
. The above equation then shows that
is negative at
, and that
cannot have any local minimum in
, so
is negative throughout. To obtain the final claim
we use an argument provided by Gergely Harcos in the comments: from the recursive relations for Bessel functions we can check that
is a positive multiple of
, and the claim then follows from the interlacing properties of the zeroes of Bessel functions.
Write , so
is positive and by Theorem 14 we have
If , then as
is negative and increasing we have
for , and thus by change of variable
for , and thus
for all . Similarly
for all . By Cauchy-Schwarz we can thus bound the integral in (30) by
and so (30) reduces to
Repeating the arguments of the previous section, we can reduce this to
and by further continuing the arguments of the previous section we end up being able to take
Also, the previous arguments allow us to take
The key inequality (11) now becomes
thus implies
whenever (32) is obeyed with the value (31) of
.

144 comments
Comments feed for this article
12 September, 2013 at 4:21 pm
Gergely Harcos
In the second display below (12), should be
should be  .
.
[Corrected, thanks – T.]
4 October, 2013 at 11:40 am
Stijn Hanson
My apologies for all the help I’m requiring but a lot of these proof techniques are new to me in style. I’m looking at your proof of the overspill principle (Lemma 7). In the part you create your
part you create your  function to be some specific function tending to infinity with x. Thus, given any
function to be some specific function tending to infinity with x. Thus, given any 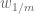 , the function
, the function 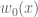 will surpass it at some point. Thus:
will surpass it at some point. Thus:
where . Upon letting x tend to infinity
. Upon letting x tend to infinity  tends to infinity and we can let m tend to infinity and we have
tends to infinity and we can let m tend to infinity and we have 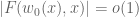 and this seems clear to me.
and this seems clear to me. is a function tending to infinity with x. Then, for all natural numbers m there is some real
is a function tending to infinity with x. Then, for all natural numbers m there is some real  such that
such that 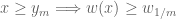 . If we define
. If we define 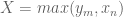 then, surely, we must have
then, surely, we must have 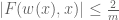 whenever
whenever  and
and 
The issue for me is the ‘sufficiently slowly’ part of the statement. Suppose that
The one thing this argument avoids is your condition of but I didn’t understand where that came from in the first place.
but I didn’t understand where that came from in the first place.
I’m sure I’ve missed something obvious (as I have before) but I can’t see it.
P.S. there is a slight typo in the proof in that it says “veifies” instead of “verifies”
4 October, 2013 at 12:14 pm
Terence Tao
One cannot conclude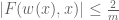 for
for  unless one already knows that
unless one already knows that  (note that
(note that  is not fixed, whereas (i) is only available for fixed w); this is why one needs
is not fixed, whereas (i) is only available for fixed w); this is why one needs 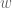 to grow more slowly than
to grow more slowly than  .
.
Incidentally, in the polymath8 writeup (see https://www.dropbox.com/s/16bei7l944twojr/newgap.pdf ) the overspill principle is no longer needed, because it turns out one can take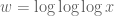 rather than have
rather than have 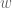 be a sufficiently slowly growing function of x.
be a sufficiently slowly growing function of x.
4 October, 2013 at 12:43 pm
Stijn Hanson
I assumed it had something to do with that w restriction but I don’t see where comes from. The way I understand it we’re setting
comes from. The way I understand it we’re setting 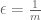 and then
and then 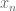 is some real number such that the
is some real number such that the  term dips below
term dips below  whenever
whenever 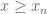 but, obviously, I must be missing something.
but, obviously, I must be missing something.
19 November, 2013 at 10:50 pm
Polymath8b: Bounded intervals with many primes, after Maynard | What's new
[…] this claim was already essentially established back in this Polymath8a post (or see Proposition 4.1 and Lemma 4.7 of the Polymath8a paper for essentially these bounds). In […]
31 July, 2014 at 8:33 am
Together and Alone, Closing the Prime Gap | For a better Vietnam
[…] work. At the time, though, this advance was one of the most fruitful ones. When the team filled in this piece of the puzzle on June 5, the bound on prime gaps dropped from about 4.6 million to […]
16 May, 2015 at 12:13 am
wanglaoxinr
for Cramér Conjecture ,change Pn to x, will that hold?
Pn means n th prime, Pn<Pn+1<=x, Max(Pn+1-Pn) means the maximum gap between two neighboring primes in (0,x], when x tending to infinity, Max(Pn+1-Pn)/(lnx)^2 tending to 1.
17 June, 2015 at 7:49 am
The prime tuples conjecture, sieve theory, and the work of Goldston-Pintz-Yildirim, Motohashi-Pintz, and Zhang | fragments
[…] for instance, if Conjecture 2 holds, then the number of twin primes less than should equal , where is the twin prime […]
29 October, 2015 at 8:06 pm
Alexey
I have a question about an upper bound of conjecture 2 (about k-tuple of primes). Where can I find a proof of this upper bound? How C_{k_0} depends from k_0?
Thank you
30 October, 2015 at 7:32 am
Terence Tao
This can be found for instance in the texts of Montgomery-Vaughan or Iwaniec-Kowalski, or any book on sieve theory (e.g. Friedlander-Iwaniec). I also have it as an application of the Selberg sieve in Exercise 34 of these notes.
5 April, 2016 at 9:38 pm
Where has the Time Gone? | Sublime Illusions
[…] Tao explains concepts wonderfully, especially if you want a summary of a long and intricate paper (like the explanation of Zhang Yitang’s work on the Twin Prime Conjecture and related backgroun…). Beware, not for the faint of […]
19 July, 2016 at 5:24 pm
John
Why is obvious that the Hardy-Littlewood infinite product does not converge to 0?
19 July, 2016 at 7:33 pm
John
Oh I guess it’s a simple consequence of the Prime Number Theorem and the discrete integration by part, i.e., let![f(p) = log[(1 - k/p) / (1 - 1/p)^k]](https://s0.wp.com/latex.php?latex=f%28p%29+%3D+log%5B%281+-+k%2Fp%29+%2F+%281+-+1%2Fp%29%5Ek%5D&bg=ffffff&fg=545454&s=0&c=20201002) , then one gets that the log of the HL-constant is equal to
, then one gets that the log of the HL-constant is equal to 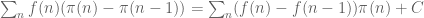 . The latter is finite since
. The latter is finite since  is bounded above and below eventually by $0.2 n / \log n$ and $5 n / \log n$.
is bounded above and below eventually by $0.2 n / \log n$ and $5 n / \log n$.