Next set of notes: Notes 1.
Kronecker is famously reported to have said, “God created the natural numbers; all else is the work of man”. The truth of this statement (literal or otherwise) is debatable; but one can certainly view the other standard number systems as (iterated) completions of the natural numbers
in various senses. For instance:
- The integers
are the additive completion of the natural numbers
(the minimal additive group that contains a copy of
).
- The rationals
are the multiplicative completion of the integers
(the minimal field that contains a copy of
).
- The reals
are the metric completion of the rationals
(the minimal complete metric space that contains a copy of
).
- The complex numbers
are the algebraic completion of the reals
(the minimal algebraically closed field that contains a copy of
).
These descriptions of the standard number systems are elegant and conceptual, but not entirely suitable for constructing the number systems in a non-circular manner from more primitive foundations. For instance, one cannot quite define the reals from scratch as the metric completion of the rationals
, because the definition of a metric space itself requires the notion of the reals! (One can of course construct
by other means, for instance by using Dedekind cuts or by using uniform spaces in place of metric spaces.) The definition of the complex numbers as the algebraic completion of the reals does not suffer from such a non-circularity issue, but a certain amount of field theory is required to work with this definition initially. For the purposes of quickly constructing the complex numbers, it is thus more traditional to first define
as a quadratic extension of the reals
, and more precisely as the extension
formed by adjoining a square root
of
to the reals, that is to say a solution to the equation
. It is not immediately obvious that this extension is in fact algebraically closed; this is the content of the famous fundamental theorem of algebra, which we will prove later in this course.
The two equivalent definitions of – as the algebraic closure, and as a quadratic extension, of the reals respectively – each reveal important features of the complex numbers in applications. Because
is algebraically closed, all polynomials over the complex numbers split completely, which leads to a good spectral theory for both finite-dimensional matrices and infinite-dimensional operators; in particular, one expects to be able to diagonalise most matrices and operators. Applying this theory to constant coefficient ordinary differential equations leads to a unified theory of such solutions, in which real-variable ODE behaviour such as exponential growth or decay, polynomial growth, and sinusoidal oscillation all become aspects of a single object, the complex exponential
(or more generally, the matrix exponential
). Applying this theory more generally to diagonalise arbitrary translation-invariant operators over some locally compact abelian group, one arrives at Fourier analysis, which is thus most naturally phrased in terms of complex-valued functions rather than real-valued ones. If one drops the assumption that the underlying group is abelian, one instead discovers the representation theory of unitary representations, which is simpler to study than the real-valued counterpart of orthogonal representations. For closely related reasons, the theory of complex Lie groups is simpler than that of real Lie groups.
Meanwhile, the fact that the complex numbers are a quadratic extension of the reals lets one view the complex numbers geometrically as a two-dimensional plane over the reals (the Argand plane). Whereas a point singularity in the real line disconnects that line, a point singularity in the Argand plane leaves the rest of the plane connected (although, importantly, the punctured plane is no longer simply connected). As we shall see, this fact causes singularities in complex analytic functions to be better behaved than singularities of real analytic functions, ultimately leading to the powerful residue calculus for computing complex integrals. Remarkably, this calculus, when combined with the quintessentially complex-variable technique of contour shifting, can also be used to compute some (though certainly not all) definite integrals of real-valued functions that would be much more difficult to compute by purely real-variable methods; this is a prime example of Hadamard’s famous dictum that “the shortest path between two truths in the real domain passes through the complex domain”.
Another important geometric feature of the Argand plane is the angle between two tangent vectors to a point in the plane. As it turns out, the operation of multiplication by a complex scalar preserves the magnitude and orientation of such angles; the same fact is true for any non-degenerate complex analytic mapping, as can be seen by performing a Taylor expansion to first order. This fact ties the study of complex mappings closely to that of the conformal geometry of the plane (and more generally, of two-dimensional surfaces and domains). In particular, one can use complex analytic maps to conformally transform one two-dimensional domain to another, leading among other things to the famous Riemann mapping theorem, and to the classification of Riemann surfaces.
If one Taylor expands complex analytic maps to second order rather than first order, one discovers a further important property of these maps, namely that they are harmonic. This fact makes the class of complex analytic maps extremely rigid and well behaved analytically; indeed, the entire theory of elliptic PDE now comes into play, giving useful properties such as elliptic regularity and the maximum principle. In fact, due to the magic of residue calculus and contour shifting, we already obtain these properties for maps that are merely complex differentiable rather than complex analytic, which leads to the striking fact that complex differentiable functions are automatically analytic (in contrast to the real-variable case, in which real differentiable functions can be very far from being analytic).
The geometric structure of the complex numbers (and more generally of complex manifolds and complex varieties), when combined with the algebraic closure of the complex numbers, leads to the beautiful subject of complex algebraic geometry, which motivates the much more general theory developed in modern algebraic geometry. However, we will not develop the algebraic geometry aspects of complex analysis here.
Last, but not least, because of the good behaviour of Taylor series in the complex plane, complex analysis is an excellent setting in which to manipulate various generating functions, particularly Fourier series (which can be viewed as boundary values of power (or Laurent) series
), as well as Dirichlet series
. The theory of contour integration provides a very useful dictionary between the asymptotic behaviour of the sequence
, and the complex analytic behaviour of the Dirichlet or Fourier series, particularly with regard to its poles and other singularities. This turns out to be a particularly handy dictionary in analytic number theory, for instance relating the distribution of the primes to the Riemann zeta function. Nowadays, many of the analytic number theory results first obtained through complex analysis (such as the prime number theorem) can also be obtained by more “real-variable” methods; however the complex-analytic viewpoint is still extremely valuable and illuminating.
We will frequently touch upon many of these connections to other fields of mathematics in these lecture notes. However, these are mostly side remarks intended to provide context, and it is certainly possible to skip most of these tangents and focus purely on the complex analysis material in these notes if desired.
Note: complex analysis is a very visual subject, and one should draw plenty of pictures while learning it. I am however not planning to put too many pictures in these notes, partly as it is somewhat inconvenient to do so on this blog from a technical perspective, but also because pictures that one draws on one’s own are likely to be far more useful to you than pictures that were supplied by someone else.
— 1. The construction and algebra of the complex numbers —
Note: this section will be far more algebraic in nature than the rest of the course; we are concentrating almost all of the algebraic preliminaries in this section in order to get them out of the way and focus subsequently on the analytic aspects of the complex numbers.
Thanks to the laws of high-school algebra, we know that the real numbers are a field: it is endowed with the arithmetic operations of addition, subtraction, multiplication, and division, as well as the additive identity
and multiplicative identity
, that obey the usual laws of algebra (i.e. the field axioms).
The algebraic structure of the reals does have one drawback though – not all (non-trivial) polynomials have roots! Most famously, the polynomial equation has no solutions over the reals, because
is always non-negative, and hence
is always strictly positive, whenever
is a real number.
As mentioned in the introduction, one traditional way to define the complex numbers is as the smallest possible extension of the reals
that fixes this one specific problem:
Definition 1 (The complex numbers) A field of complex numbers is a field
that contains the real numbers
as a subfield, as well as a root
of the equation
. (Thus, strictly speaking, a field of complex numbers is a pair
, but we will almost always abuse notation and use
as a metonym for the pair
.) Furthermore,
is generated by
and
, in the sense that there is no subfield of
, other than
itself, that contains both
and
; thus, in the language of field extensions, we have
.
(We will take the existence of the real numbers as a given in this course; constructions of the real number system can of course be found in many real analysis texts, including my own.)
Definition 1 is short, but proposing it as a definition of the complex numbers raises some immediate questions:
- (Existence) Does such a field
even exist?
- (Uniqueness) Is such a field
unique (up to isomorphism)?
- (Non-arbitrariness) Why the square root of
? Why not adjoin instead, say, a fourth root of
, or the solution to some other algebraic equation? Also, could one iterate the process, extending
further by adding more roots of equations?
The third set of questions can be answered satisfactorily once we possess the fundamental theorem of algebra. For now, we focus on the first two questions.
We begin with existence. One can construct the complex numbers quite explicitly and quickly using the Argand plane construction; see Remark 7 below. However, from the perspective of higher mathematics, it is more natural to view the construction of the complex numbers as a special case of the more general algebraic construction that can extend any field by the root
of an irreducible nonlinear polynomial
over that field; this produces a field of complex numbers
when specialising to the case where
and
. We will just describe this construction in that special case, leaving the general case as an exercise.
Starting with the real numbers , we can form the space
of (formal) polynomials
with real co-efficients and arbitrary non-negative integer
in one indeterminate variable
. (A small technical point: we do not view this indeterminate
as belonging to any particular domain such as
, so we do not view these polynomials
as functions but merely as formal expressions involving a placeholder symbol
(which we have rendered in Roman type to indicate its formal character). In this particular characteristic zero setting of working over the reals, it turns out to be harmless to identify each polynomial
with the corresponding function
formed by interpreting the indeterminate
as a real variable; but if one were to generalise this construction to positive characteristic fields, and particularly finite fields, then one can run into difficulties if polynomials are not treated formally, due to the fact that two distinct formal polynomials might agree on all inputs in a given finite field (e.g. the polynomials
and
agree for all
in the finite field
). However, this subtlety can be ignored for the purposes of this course.) This space
of polynomials has a pretty good algebraic structure, in particular the usual operations of addition, subtraction, and multiplication on polynomials, together with the zero polynomial
and the unit polynomial
, give
the structure of a (unital) commutative ring. This commutative ring also contains
as a subring (identifying each real number
with the degree zero polynomial
), and so we shall henceforth omit the
factor when referring to elements of
. The ring
is however not a field, because many non-zero elements of
do not have multiplicative inverses. (In fact, no non-constant polynomial in
has an inverse in
, because the product of two non-constant polynomials has a degree that is the sum of the degrees of the factors.)
If a unital commutative ring fails to be a field, then it will instead possess a number of non-trivial ideals. The only ideal we will need to consider here is the principal ideal
This is clearly an ideal of – it is closed under addition and subtraction, and the product of any element of the ideal
with an element of the full ring
remains in the ideal
.
We now define to be the quotient space
of the commutative ring by the ideal
; this is the space of cosets
of
in
. Because
is an ideal, there is an obvious way to define addition, subtraction, and multiplication in
, namely by setting
and
for all ; these operations, together with the additive identity
and the multiplicative identity
, can be easily verified to give
the structure of a commutative ring. Also, the real line
embeds into
by identifying each real number
with the coset
; note that this identification is injective, as no real number is a multiple of the polynomial
.
If we define to be the coset
then it is clear from construction that . Thus
contains both
and a solution of the equation
. Also, since every element of
is of the form
for some polynomial
, we see that every element of
is a polynomial combination
of
with real coefficients; in particular, any subring of
that contains
and
will necessarily have to contain every element of
. Thus
is generated by
and
.
The only remaining thing to verify is that is a field and not just a commutative ring. In other words, we need to show that every non-zero element of
has a multiplicative inverse. This stems from a particular property of the polynomial
, namely that it is irreducible in
. That is to say, we cannot factor
into non-constant polynomials
with . Indeed, as
has degree two, the only possible way such a factorisation could occur is if
both have degree one, which would imply that the polynomial
has a root in the reals
, which of course it does not.
Because the polynomial is irreducible, it is also prime: if
divides a product
of two polynomials in
, then it must also divide at least one of the factors
,
. Indeed, if
does not divide
, then by irreducibility the greatest common divisor of
and
is
. Applying the Euclidean algorithm for polynomials, we then obtain a representation of
as
for some polynomials ; multiplying both sides by
, we conclude that
is a multiple of
.
Since is prime, the quotient space
is an integral domain: there are no zero-divisors in
other than zero. This brings us closer to the task of showing that
is a field, but we are not quite there yet; note for instance that
is an integral domain, but not a field. But one can finish up by using finite dimensionality. As
is a ring containing the field
, it is certainly a vector space over
; as
is generated by
and
, and
, we see that it is in fact a two-dimensional vector space over
, spanned by
and
(which are linearly independent, as
clearly cannot be real). In particular, it is finite dimensional. For any non-zero
, the multiplication map
is an
-linear map from this finite-dimensional vector space to itself. As
is an integral domain, this map is injective; by finite-dimensionality, it is therefore surjective (by the rank-nullity theorem). In particular, there exists
such that
, and hence
is invertible and
is a field. This concludes the construction of a complex field
.
Remark 2 One can think of the action of passing from a ring
to a quotient
by some ideal
as the action of forcing some relations to hold between the various elements of
, by requiring all the elements of the ideal
(or equivalently, all the generators of
) to vanish. Thus one can think of
as the ring formed by adjoining a new element
to the existing ring
and then demanding the constraint
. With this perspective, the main issues to check in order to obtain a complex field are firstly that these relations do not collapse the ring so much that two previously distinct elements of
become equal, and secondly that all the non-zero elements become invertible once the relations are imposed, so that we obtain a field rather than merely a ring or integral domain.
Remark 3 It is instructive to compare the complex field
, formed by adjoining the square root of
to the reals, with other commutative rings such as the dual numbers
(which adjoins an additional square root of
to the reals) or the split complex numbers
(which adjoins a new root of
to the reals). The latter two objects are perfectly good rings, but are not fields (they contain zero divisors, and the first ring even contains a nilpotent). This is ultimately due to the reducible nature of the polynomials
and
in
.
Uniqueness of up to isomorphism is a straightforward exercise:
Exercise 4 (Uniqueness up to isomorphism) Suppose that one has two complex fields
and
. Show that there is a unique field isomorphism
that maps
to
and is the identity on
.
Now that we have existence and uniqueness up to isomorphism, it is safe to designate one of the complex fields as the complex field; the other complex fields out there will no longer be of much importance in this course (or indeed, in most of mathematics), with one small exception that we will get to later in this section. One can, if one wishes, use the above abstract algebraic construction
as the choice for “the” complex field
, but one can certainly pick other choices if desired (e.g. the Argand plane construction in Remark 7 below). But in view of Exercise 4, the precise construction of
is not terribly relevant for the purposes of actually doing complex analysis, much as the question of whether to construct the real numbers
using Dedekind cuts, equivalence classes of Cauchy sequences, or some other construction is not terribly relevant for the purposes of actually doing real analysis. So, from here on out, we will no longer refer to the precise construction of
used; the reader may certainly substitute his or her own favourite construction of
in place of
if desired, with essentially no change to the rest of the lecture notes.
Exercise 5 Let
be an arbitrary field, let
be the ring of polynomials with coefficients in
, and let
be an irreducible polynomial in
of degree at least two. Show that
is a field containing an embedded copy of
, as well as a root
of the equation
, and that this field is generated by
and
. Also show that all such fields are unique up to isomorphism. (This field
is an example of a field extension of
, the further study of which can be found in any advanced undergraduate or early graduate text on algebra, and is the starting point in particular for the beautiful topic of Galois theory, which we will not discuss here.)
Exercise 6 Let
be an arbitrary field. Show that every non-constant polynomial
in
can be factored as the product
of irreducible non-constant polynomials. Furthermore show that this factorisation is unique up to permutation of the factors
, and multiplication of each of the factors by a constant (with the product of all such constants being one). In other words: the polynomial ring
is a unique factorisation domain.
Remark 7 (Real and imaginary coordinates) As a complex field
is spanned (over
) by the linearly independent elements
and
, we can write
with each element
of
having a unique representation of the form
, thus
for real
. The addition, subtraction, and multiplication operations can then be written down explicitly in these coordinates as
and with a bit more work one can compute the division operation as
if
. One could take these coordinate representations as the definition of the complex field
and its basic arithmetic operations, and this is indeed done in many texts introducing the complex numbers. In particular, one could take the Argand plane
as the choice of complex field, where we identify each point
in
with
(so for instance
becomes endowed with the multiplication operation
). This is a very concrete and direct way to construct the complex numbers; the main drawback is that it is not immediately obvious that the field axioms are all satisfied. For instance, the associativity of multiplication is rather tedious to verify in the coordinates of the Argand plane. In contrast, the more abstract algebraic construction of the complex numbers given above makes it more evident what the source of the field structure on
is, namely the irreducibility of the polynomial
.
Remark 8 Because of the Argand plane construction, we will sometimes refer to the space
of complex numbers as the complex plane. We should warn, though, that in some areas of mathematics, particularly in algebraic geometry,
is viewed as a one-dimensional complex vector space (or a one-dimensional complex manifold or complex variety), and so
is sometimes referred to in those cases as a complex line. (Similarly, Riemann surfaces, which from a real point of view are two-dimensional surfaces, can sometimes be referred to as complex curves in the literature; the modular curve is a famous instance of this.) In this current course, though, the topological notion of dimension turns out to be more important than the algebraic notions of dimension, and as such we shall generally refer to
as a plane rather than a line.
Elements of of the form
for
real are known as purely imaginary numbers; the terminology is colourful, but despite the name, imaginary numbers have precisely the same first-class mathematical object status as real numbers. If
is a complex number, the real components
of
are known as the real part
and imaginary part
of
respectively. Complex numbers that are not real are occasionally referred to as strictly complex numbers. In the complex plane, the set
of real numbers forms the real axis, and the set
of imaginary numbers forms the imaginary axis. Traditionally, elements of
are denoted with symbols such as
,
, or
, while symbols such as
are typically intended to represent real numbers instead.
Remark 9 We noted earlier that the equation
had no solutions in the reals because
was always positive. In other words, the properties of the order relation
on
prevented the existence of a root for the equation
. As
does have a root for
, this means that the complex numbers
cannot be ordered in the same way that the reals are ordered (that is to say, being totally ordered, with the positive numbers closed under both addition and multiplication). Indeed, one usually refrains from putting any order structure on the complex numbers, so that statements such as
for complex numbers
are left undefined (unless
are real, in which case one can of course use the real ordering). In particular, the complex number
is considered to be neither positive nor negative, and an assertion such as
is understood to implicitly carry with it the claim that
are real numbers and not just complex numbers. (Of course, if one really wants to, one can find some total orderings to place on
, e.g. lexicographical ordering on the real and imaginary parts. However, such orderings do not interact too well with the algebraic structure of
and are rarely useful in practice.)
As with any other field, we can raise a complex number to a non-negative integer
by declaring inductively
and
for
; in particular we adopt the usual convention that
(when thinking of the base
as a complex number, and the exponent
as a non-negative integer). For negative integers
, we define
for non-zero
; we leave
undefined when
is zero and
is negative. At the present time we do not attempt to define
for any exponent
other than an integer; we will return to such exponentiation operations later in the course, though we will at least define the complex exponential
for any complex
later in this set of notes.
By definition, a complex field is a field
together with a root
of the equation
. But if
is a root of the equation
, then so is
(indeed, from the factorisation
we see that these are the only two roots of this quadratic equation. Thus we have another complex field
which differs from
only in the choice of root
. By Exercise 4, there is a unique field isomorphism from
to
that maps
to
(i.e. a complex field isomorphism from
to
); this operation is known as complex conjugation and is denoted
. In coordinates, we have
Being a field isomorphism, we have in particular that
and
for all complex numbers . It is also clear that complex conjugation fixes the real numbers, and only the real numbers:
if and only if
is real. Geometrically, complex conjugation is the operation of reflection in the complex plane across the real axis. It is clearly an involution in the sense that it is its own inverse:
One can also relate the real and imaginary parts to complex conjugation via the identities
Remark 10 Any field automorphism of
has to map
to a root of
, and so the only field automorphisms of
that preserve the real line are the identity map and the conjugation map; conversely, the real line is the subfield of
fixed by both of these automorphisms. In the language of Galois theory, this means that
is a Galois extension of
, with Galois group
consisting of two elements. There is a certain sense in which one can think of the complex numbers (or more precisely, the scheme
of complex numbers) as a double cover of the real numbers (or more precisely, the scheme
of real numbers), analogous to how the boundary of a Möbius strip can be viewed as a double cover of the unit circle formed by shrinking the width of the strip to zero. (In this analogy, points on the unit circle correspond to specific models of the real number system
, and lying above each such point are two specific models
,
of the complex number system; this analogy can be made precise using Grothendieck’s “functor of points” interpretation of schemes.) The operation of complex conjugation is then analogous to the operation of monodromy caused by looping once around the base unit circle, causing the two complex fields sitting above a real field to swap places with each other. (This analogy is not quite perfect, by the way, because the boundary of a Möbius strip is not simply connected and can in turn be finitely covered by other curves, whereas the complex numbers are algebraically complete and admit no further finite extensions; one should really replace the unit circle here by something with a two-element fundamental group, such as the projective plane
that is double covered by the sphere
, but this is harder to visualize.) The analogy between (absolute) Galois groups and fundamental groups suggested by this picture can be made precise in scheme theory by introducing the concept of an étale fundamental group, which unifies the two concepts, but developing this further is well beyond the scope of this course; see this book of Szamuely for further discussion.
Observe that if we multiply a complex number by its complex conjugate
, we obtain a quantity
which is invariant with respect to conjugation (i.e.
) and is therefore real. The map
produced this way is known in field theory as the norm form of
over
; it is clearly multiplicative in the sense that
, and is only zero when
is zero. It can be used to link multiplicative inversion with complex conjugation, in that we clearly have
for any non-zero complex number . In coordinates, we have
(thus recovering, by the way, the inversion formula implicit in Remark 7). In coordinates, the multiplicativity
takes the form of Lagrange’s identity
— 2. The geometry of the complex numbers —
The norm form of the complex numbers has the feature of being positive definite:
is always non-negative (and strictly positive when
is non-zero). This is a feature that is somewhat special to the complex numbers; for instance, the quadratic extension
of the rationals
by
has the norm form
, which is indefinite. One can view this positive definiteness of the norm form as the one remaining vestige in
of the order structure
on the reals, which as remarked previously is no longer present directly in the complex numbers. (One can also view the positive definiteness of the norm form as a consequence of the topological connectedness of the punctured complex plane
: the norm form is positive at
, and cannot change sign anywhere in
, so is forced to be positive on the rest of this connected region.)
One consequence of positive definiteness is that the bilinear form
becomes a positive definite inner product on (viewed as a vector space over
). In particular, this turns the complex numbers into an inner product space over the reals. From the usual theory of inner product spaces, we can then construct a norm
(thus, the norm is the square root of the norm form) which obeys the triangle inequality
(which implies the usual permutations of this inequality, such as ), and from the multiplicativity of the norm form we also have
(and hence also if
is non-zero) and from the involutive nature of complex conjugation we have
The norm clearly extends the absolute value operation
on the real numbers, and so we also refer to the norm
of a complex number
as its absolute value or magnitude. In coordinates, we have
thus for instance , and from (6) we also immediately have the useful inequalities
As with any other normed vector space, the norm defines a metric on the complex numbers via the definition
Note that using the Argand plane representation of as
that this metric coincides with the usual Euclidean metric on
. This metric in turn defines a topology on
(generated in the usual manner by the open disks
), which in turn generates all the usual topological notions such as the concept of an open set, closed set, compact set, connected set, and boundary of a set; the notion of a limit of a sequence
; the notion of a continuous map, and so forth. For instance, a sequence
of complex numbers converges to a limit
if
as
, and a map
is continuous if one has
whenever
, or equivalently if the inverse image of any open set is open. Again, using the Argand plane representation, these notions coincide with their counterparts on the Euclidean plane
.
As usual, if a sequence of complex numbers converges to a limit
, we write
. From the triangle inequality (3) and the multiplicativity property (4) we see that the addition operation
, subtraction operation
, and multiplication operation
, thus we have the familiar limit laws
and
whenever the limits on the right-hand side exist. Similarly, from (5) we see that complex conjugation is an isometry of the complex numbers, thus
when the limit on the right-hand side exists. As a consequence, the norm form and the absolute value
are also continuous, thus
whenever the limit on the right-hand side exists. Using the formula (2) for the reciprocal of a complex number, we also see that division is a continuous operation as long as the denominator is non-zero, thus
as long as the limits on the right-hand side exist, and the limit in the denominator is non-zero.
From (7) we see that
in particular
and
whenever the limit on the right-hand side exists. One consequence of this is that is complete: every sequence
of complex numbers that is a Cauchy sequence (thus
as
) converges to a unique complex limit
. (As such, one can view the complex numbers as a (very small) example of a Hilbert space.)
As with the reals, we have the fundamental fact that any formal series of complex numbers which is absolutely convergent, in the sense that the non-negative series
is finite, is necessarily convergent to some complex number
, in the sense that the partial sums
converge to
as
. This is because the triangle inequality ensures that the partial sums are a Cauchy sequence. As usual we write
to denote the assertion that
is the limit of the partial sums
. We will occasionally have need to deal with series that are only conditionally convergent rather than absolutely convergent, but in most of our applications the only series we will actually evaluate are the absolutely convergent ones. Many of the limit laws imply analogues for series, thus for instance
whenever the series on the right-hand side is absolutely convergent (or even just convergent). We will not write down an exhaustive list of such series laws here.
An important role in complex analysis is played by the unit circle
In coordinates, this is the set of points for which
, and so this indeed has the geometric structure of a unit circle. Elements of the unit circle will be referred to in these notes as phases. Every non-zero complex number
has a unique polar decomposition as
where
is a positive real and
lies on the unit circle
. Indeed, it is easy to see that this decomposition is given by
and
, and that this is the only polar decomposition of
. We refer to the polar components
and
of a non-zero complex number
as the magnitude and phase of
respectively.
From (4) we see that the unit circle is a multiplicative group; it contains the multiplicative identity
, and if
lie in
, then so do
and
. From (2) we see that reciprocation and complex conjugation agree on the unit circle, thus
for . It is worth emphasising that this useful identity does not hold as soon as one leaves the unit circle, in which case one must use the more general formula (2) instead! If
are non-zero complex numbers
with polar decompositions
and
respectively, then clearly the polar decompositions of
and
are given by
and
respectively. Thus polar coordinates are very convenient for performing complex multiplication, although they turn out to be atrocious for performing complex addition. (This can be contrasted with the usual Cartesian coordinates
, which are very convenient for performing complex addition and mildly inconvenient for performing complex multiplication.) In the language of group theory, the polar decomposition splits the multiplicative complex group
as the direct product of the positive reals
and the unit circle
:
.
If is an element of the unit circle
, then from (4) we see that the operation
of multiplication by
is an isometry of
, in the sense that
for all complex numbers . This isometry also preserves the origin
. As such, it is geometrically obvious (see Exercise 11 below) that the map
must either be a rotation around the origin, or a reflection around a line. The former operation is orientation preserving, and the latter is orientation reversing. Since the map
is clearly orientation preserving when
, and the unit circle
is connected, a continuity argument shows that
must be orientation preserving for all
, and so must be a rotation around the origin by some angle. Of course, by trigonometry, we may write
for some real number . The rotation
clearly maps the number
to the number
, and so the rotation must be a counter-clockwise rotation by
(adopting the usual convention of placing
to the right of the origin and
above it). In particular, when applying this rotation
to another point
on the unit circle, this point must get rotated to
. We have thus given a geometric proof of the multiplication formula
taking real and imaginary parts, we recover the familiar trigonometric addition formulae
We can also iterate the multiplication formula to give de Moivre’s formula
for any natural number (or indeed for any integer
), which can in turn be used to recover familiar identities such as the double angle formulae
or triple angle formulae
after expanding out de Moivre’s formula for or
and taking real and imaginary parts.
- (i) Let
be an isometry of the Euclidean plane that fixes the origin
. Show that
is either a rotation around the origin by some angle
, or the reflection around some line through the origin. (Hint: try to compose
with rotations or reflections to achieve some normalisation of
, e.g. that
fixes
. Then consider what
must do to other points in the plane, such as
. Alternatively, one can use various formulae relating distances to angle, such as the sine rule or cosine rule, or the formula
for the inner product.) For this question, you may use any result you already know from Euclidean geometry or trigonometry.
- (ii) Show that all isometries
of the complex numbers take the form
or
for some complex number
and phase
.
Every non-zero complex number can now be written in polar form as
with and
; we refer to
as an argument of
, and can be interpreted as an angle of counterclockwise rotation needed to rotate the positive real axis to a position that contains
. The argument is not quite unique, due to the periodicity of sine and cosine: if
is an argument of
, then so is
for any integer
, and conversely these are all the possible arguments that
can have. The set of all such arguments will be denoted
; it is a coset of the discrete group
, and can thus be viewed as an element of the
-torus
.
The operation of multiplying a complex number
by a given non-zero complex number
now has a very appealing geometric interpretation when expressing
in polar coordinates (9): this operation is the composition of the operation of dilation by
around the origin, and counterclockwise rotation by
around the origin. For instance, multiplication by
performs a counter-clockwise rotation by
around the origin, while multiplication by
performs instead a clockwise rotation by
. As complex multiplication is commutative and associative, it does not matter in which order one performs the dilation and rotation operations. Similarly, using Cartesian coordinates, we see that the operation
of adding a complex number
by a given complex number
is simply a spatial translation by a displacement of
. The multiplication operation need not be isometric (due to the presence of the dilation
), but observe that both the addition and multiplication operations are conformal (angle-preserving) and also orientation-preserving (a counterclockwise loop will transform to another counterclockwise loop, and similarly for clockwise loops). As we shall see later, these conformal and orientation-preserving properties of the addition and multiplication maps will extend to the larger class of complex differentiable maps (at least outside of critical points of the map), and are an important aspect of the geometry of such maps.
Remark 12 One can also interpret the operations of complex arithmetic geometrically on the Argand plane as follows. As the addition law on
coincides with the vector addition law on
, addition and subtraction of complex numbers is given by the usual parallelogram rule for vector addition; thus, to add a complex number
to another
, we can translate the complex plane until the origin
gets mapped to
, and then
gets mapped to
; conversely, subtraction by
corresponds to translating
back to
. Similarly, to multiply a complex number
with another
, we can dilate and rotate the complex plane around the origin until
gets mapped to
, and then
will be mapped to
; conversely, division by
corresponds to dilating and rotating
back to
.
When performing computations, it is convenient to restrict the argument of a non-zero complex number
to lie in a fundamental domain of the
-torus
, such as the half-open interval
or
, in order to recover a unique parameterisation (at the cost of creating a branch cut at one point of the unit circle). Traditionally, the fundamental domain that is most often used is the half-open interval
. The unique argument of
that lies in this interval is called the standard argument of
and is denoted
, and
is called the standard branch of the argument function. Thus for instance
,
,
, and
. Observe that the standard branch of the argument has a discontinuity on the negative real axis
, which is the branch cut of this branch. Changing the fundamental domain used to define a branch of the argument can move the branch cut around, but cannot eliminate it completely, due to non-trivial monodromy (if one continuously loops once counterclockwise around the origin, and varies the argument continuously as one does so, the argument will increment by
, and so no branch of the argument function can be continuous at every point on the loop).
The multiplication formula (8) resembles the multiplication formula
for the real exponential function . The two formulae can be unified through the famous Euler formula involving the complex exponential
. There are many ways to define the complex exponential. Perhaps the most natural is through the ordinary differential equation
with boundary condition
. However, as we have not yet set up a theory of complex differentiation, we will proceed (at least temporarily) through the device of Taylor series. Recalling that the real exponential function
has the Taylor expansion
which is absolutely convergent for any real , one is led to define the complex exponential function
by the analogous expansion
noting from (4) that the absolute convergence of the real exponential for any
implies the absolute convergence of the complex exponential for any
. We also frequently write
for
. The multiplication formula (10) for the real exponential extends to the complex exponential:
Exercise 13 Use the binomial theorem and Fubini’s theorem for (complex) doubly infinite series to conclude that
for any complex numbers
.
If one compares the Taylor series for with the familiar Taylor expansions
and
for the (real) sine and cosine functions, one obtains the Euler formula
for any real number ; in particular we have the famous identities
We now see that the multiplication formula (8) can be written as a special form
of (12); similarly, de Moivre’s formula takes the simple and intuitive form
From (12) and (13) we also see that the exponential function basically transforms Cartesian coordinates to polar coordinates:
Later on in the course we will study (the various branches of) the logarithm function that inverts the complex exponential, thus converting polar coordinates back to Cartesian ones.
From (13) and (1), together with the easily verified identity
we see that we can recover the trigonometric functions from the complex exponential by the formulae
(Indeed, if one wished, one could take these identities as the definition of the sine and cosine functions, giving a purely analytic way to construct these trigonometric functions.) From these identities one can derive all the usual trigonometric identities from the basic properties of the exponential (and in particular (12)). For instance, using a little bit of high school algebra we can prove the familiar identity
from (16):
Thus, in principle at least, one no longer has a need to memorize all the different trigonometric identities out there, since they can now all be unified as consequences of just a handful of basic identities for the complex exponential, such as (12), (14), and (15).
In view of (16), it is now natural to introduce the complex sine and cosine functions and
by the formula
These complex trigonometric functions no longer have a direct trigonometric interpretation (as one cannot easily develop a theory of complex angles), but they still inherit almost all of the algebraic properties of their real-variable counterparts. For instance, one can repeat the above high school algebra computations verbatim to conclude that
for all . (We caution however that this does not imply that
and
are bounded in magnitude by
– note carefully the lack of absolute value signs outside of
and
in the above formula! See also Exercise 16 below.) Similarly for all of the other trigonometric identities. (Later on in this series of lecture notes, we will develop the concept of analytic continuation, which can explain why so many real-variable algebraic identities naturally extend to their complex counterparts.) From (11) we see that the complex sine and cosine functions have the same Taylor series expansion as their real-variable counterparts, namely
and
The formulae (17) for the complex sine and cosine functions greatly resemble those of the hyperbolic trigonometric functions , defined by the formulae
Indeed, if we extend these functions to the complex domain by defining to be the functions
then on comparison with (17) we obtain the complex identities
for all complex . Thus we see that once we adopt the perspective of working over the complex numbers, the hyperbolic trigonometric functions are “rotations by 90 degrees” of the ordinary trigonometric functions; this is a simple example of what physicists call a Wick rotation. In particular, we see from these identities that any trigonometric identity will have a hyperbolic counterpart, though due to the presence of various factors of
, the signs may change as one passes from trigonometric to hyperbolic functions or vice versa (a fact quantified by Osborne’s rule). For instance, by substituting (19) or (20) into (18) (and replacing
by
or
as appropriate), we end up with the analogous identity
for the hyperbolic trigonometric functions. Similarly for all other trigonometric identities. Thus we see that the complex exponential single-handedly unites the trigonometry, hyperbolic trigonometry, and the real exponential function into a single coherent theory!
Exercise 14
- (i) If
is a positive integer, show that the only complex number solutions to the equation
are given by the
complex numbers
for
; these numbers are thus known as the
roots of unity. Conclude the identity
for any complex number
.
- (ii) Show that the only compact subgroups
of the multiplicative complex numbers
are the unit circle
and the
roots of unity
for
. (Hint: there are two cases, depending on whether
is a limit point of
or not.)
- (iii) Give an example of a non-compact subgroup of
.
- (iv) Show that the only closed subgroups of the additive group
are the whole group
, the trivial group
, and groups of the form
for some non-zero real
. (Hint: divide into cases, depending on whether
is isolated or not.)
- (v) Show that the only connected closed subgroups of
are the whole group
, the trivial group
, and the lines
for some non-zero complex number
. (Hint: modify the argument of (iv), and if the subgroup contains a line, try to “quotient it out” to reduce back to a one-dimensional problem.)
- (vi) Show that the only closed subgroups of
are either
, discrete (every point is isolated), a line
for some non-zero complex number
, or of the form
where
are non-zero complex numbers that are linearly independent over the reals.
- (vii) Show that the only connected closed subgroups of
are the whole group
, the trivial group
, and the one-parameter groups of the form
for some non-zero complex number
. (Hint: apply (vi) to the inverse image of the group under the exponential map.)
The next exercise gives a special case of the fundamental theorem of algebra, when considering the roots of polynomials of the specific form .
Exercise 15 Show that if
is a non-zero complex number and
is a positive integer, then there are exactly
distinct solutions to the equation
, and any two such solutions differ (multiplicatively) by an
root of unity. In particular, a non-zero complex number
has two square roots, each of which is the negative of the other. What happens when
?
Exercise 16 Let
be a sequence of complex numbers. Show that
is bounded if and only if the imaginary part of
is bounded, and similarly with
replaced by
.
Exercise 17 (This question was drawn from a previous version of this course taught by Rowan Killip.) Let
be distinct complex numbers, and let
be a positive real that is not equal to
.
- (i) Show that the set
defines a circle in the complex plane. (Ideally, you should be able to do this without breaking everything up into real and imaginary parts.)
- (ii) Conversely, show that every circle in the complex plane arises in such a fashion (for suitable choices of
, of course).
- (iii) What happens if
?
- (iv) Let
be a circle that does not pass through the origin. Show that the image of
under the inversion map
is a circle. What happens if
is a line? What happens if the
passes through the origin (and one then deletes the origin from
before applying the inversion map)?
Exercise 18 If
is a complex number, show that
.

64 comments
Comments feed for this article
18 September, 2016 at 2:23 pm
scottedwards2000
Reblogged this on The Order of SQL.
18 September, 2016 at 2:24 pm
Vadiraja
Perhaps we should add that are the classes of
are the classes of  . We should avoid using the symbol
. We should avoid using the symbol  and identifying the field
and identifying the field 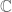 as the ring
as the ring ![\mathbb{R}[i]](https://s0.wp.com/latex.php?latex=%5Cmathbb%7BR%7D%5Bi%5D&bg=ffffff&fg=545454&s=0&c=20201002) modulo the relation that
modulo the relation that 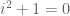 .
.
Its the same thing, of course as your previous definition![\mathbb{C}=R[i]/(i^2+1)](https://s0.wp.com/latex.php?latex=%5Cmathbb%7BC%7D%3DR%5Bi%5D%2F%28i%5E2%2B1%29&bg=ffffff&fg=545454&s=0&c=20201002) since
since  is the smallest ideal containing the relation
is the smallest ideal containing the relation 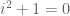 .
.
Adding this concept of a ring modulo relations, when people might be learning about quotient rings for the first time, is confusing.
[Remark about rings with relations added -T.]
18 September, 2016 at 2:43 pm
Anonymous
It is interesting to observe that is defined only as a root of
is defined only as a root of 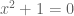 , hence any identity involving
, hence any identity involving  (e.g. Euler formula) automatically(!) holds also for the other root (i.e.
(e.g. Euler formula) automatically(!) holds also for the other root (i.e.  may be replaced by
may be replaced by 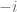 in the identity).
in the identity).
19 September, 2016 at 5:19 am
Anonymous
A priori, only any *algebraic* identity involving i. For instance, exp(pi/2 * -i)=/=exp(pi/2 * i).
19 September, 2016 at 6:51 am
Anonymous
More precisely, if there is a proof for any(!) identity involving “i” (which needs merely to satisfy ), then the proof should apply also for “-i” (replacing “i”).
), then the proof should apply also for “-i” (replacing “i”).
19 September, 2016 at 10:29 am
Anonymous
I think the point could be concisely phrased as “complex conjugation is a field automorphism.”
18 September, 2016 at 3:07 pm
Fred Lunnon
For “half-open interval {\{ \theta: \pi < \theta \leq \pi \}} "
read "half-open interval {\{ \theta: -\pi < \theta \leq \pi \}} "
For "the (various branches of the) logarithm "
read "(the various branches of) the logarithm "
WFL
[Corrected, thanks – T.]
18 September, 2016 at 7:47 pm
Lior Silberman
After multiplication by is rotation by
is rotation by 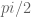 counter-clockwise, multiplication by
counter-clockwise, multiplication by 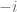 is rotation by
is rotation by 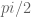 clockwise, but the text has “rotation by i”
clockwise, but the text has “rotation by i”
[Corrected, thanks – T.]
18 September, 2016 at 11:17 pm
The Birdwatcher
“For instance, one cannot quite define the reals {{\bf R}} from scratch as the metric completion of the rationals {{\bf Q}}, because the definition of a metric space itself requires the notion of the reals”
One can certainly view it as the completion as a uniform space (the two main uses of uniform spaces (that I know of) are (i) the elimination of this circularity and (ii) unifying the exposition of metric completions and module completions (the ones that allow us to talk formal power series in AG))
[Note about uniform space and Dedekind cut construction of the reals added. I had thought about mentioning that the reals can also be viewed as the order-theoretic completion of the rationals, which is what the Dedekind cut construction essentially is capturing, but since the extended reals![[-\infty,\infty]](https://s0.wp.com/latex.php?latex=%5B-%5Cinfty%2C%5Cinfty%5D&bg=ffffff&fg=545454&s=0&c=20201002) are arguably another candidate for this order-theoretic completion, I could not figure out how to insert this comment succinctly without disrupting the flow of the discussion. -T]
are arguably another candidate for this order-theoretic completion, I could not figure out how to insert this comment succinctly without disrupting the flow of the discussion. -T]
19 September, 2016 at 3:46 am
Juha-Matti Perkkiö
Indeed, and Dedekind cuts are very elementary, non-circular and not relying on any auxiliary concepts. (I was wondering about the purpose of the comment on circularity as well.)
By the way, there is one philosophical/pedagogical aspect of complex numbers which might be relevant at this level of discussion. Namely, the geometric construction (with compass and straight edge) of the product of two complex numbers is generically simpler and never more complicated than for two real numbers. Perhaps the notion of scaling by a real factor is so deceptively familiar that this curious little fact is easily overlooked.
[Remark added on the geometric interpretation of the complex arithmetic operations – T.]
21 September, 2016 at 9:04 am
Anonymous
Arguably the fastest way to construct the reals as an ordered field directly from the integers, by-passing the rationals completely, is to define them as “slopes” in the sense of Eudoxus, i.e. quasimorphisms from Z to Z up to bounded distance. It is a pity that the infinitely more clumsy definition via Dedekind cuts seems to have become the standard one.
18 September, 2016 at 11:21 pm
Mikhail Katz
Terry, Kronecker famously DID NOT write this. A colleague of his named Weber claimed that Kronecker made such a comment in a lecture. The lecture itself was never published and we have no way of checking the accuracy of this quote. Kronecker scholar Yvon Gauthier believes the attribution is dubious because what Kronecker specifically did write is that numbers are a product of the human mind. The implied realism about number systems just does not seem to square well with Kronecker’s views on infinity and specifically his rejection of completed infinity.
[Attribution reworded – T.]
19 September, 2016 at 12:47 am
Anonymous
Typo in the Lagrange formula at end of section 1; s/ab-cd/ac-bd/
[Corrected, thanks – T.]
19 September, 2016 at 3:44 am
Joerg Grande
In Exercise 10 (iii), did you confuse the unit circle and the complex multiplicative group?
[I don’t believe so – T.]
19 September, 2016 at 4:12 am
Anonymous
The accent in “etalé fundamental group” is on the wrong e (it should be étale)
[Corrected, thanks – T.]
19 September, 2016 at 1:44 pm
Bo Jacoby
Elementary arithmetic notation can be somewhat simplified. Knowing addition, multiplication and exponentiation you do not need a subtraction operation or a division bar or a square root sign, because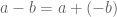 and
and  and
and  . When the minus sign is no longer used for subtraction but only for change of sign, you may write
. When the minus sign is no longer used for subtraction but only for change of sign, you may write 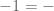 , and the above expressions become
, and the above expressions become  ,
,  , and
, and 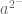 . You do not need a multiplication sign because the product
. You do not need a multiplication sign because the product 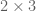 can be written
can be written . Also the expression
. Also the expression  is conveniently written
is conveniently written  , emphasizing the fact that it is algebraic when x is rational.
, emphasizing the fact that it is algebraic when x is rational.
19 September, 2016 at 5:37 pm
Moshe Simon
The residue calculus and contour integration are indeed magical, which makes them difficult to understand intuitively. Many of the results that are traditionally proved using them are topological in nature, and can be derived using other, topological, arguments that follow from the idea that a complex differentiable function is locally a rotation composed with a radial scaling, and thus does no folding locally or globally. These arguments utilize the concept of the winding number of a closed curve around any point not on the curve, which has a natural definition derived from any continuous branch of the argument of the points on the curve. Among the results that can be obtained (not necessarily in this order) are:
Min-Max modulus principle.
Algebraic closure of C.
Analyticity of differentiable functions.
The fixed point theorem for continuous functions on a disc.
The covering theorem.
Liouville’s theorem.
Schwartz lemma.
Cauchy’s inequality.
Open map theorem.
21 September, 2016 at 12:17 am
Anonymous
The third result can be viewed as “one half” of the equivalence between holomorphic (i.e. locally complex differentiable) functions and analytic (i.e. local representation by Taylor series) functions.
21 September, 2016 at 5:46 am
Edward C. Jones
Is there a paper or text where this approach to complex variables is worked out?
21 September, 2016 at 9:16 am
Moshe Simon
G.T. Whyburn Topological Analysis
A.F. Beardon Complex Analysis: The Argument Principle in Analysis and Topology
I also have course notes from lectures given by Beardon many years ago.
20 September, 2016 at 12:45 am
Anonymous
Euler’s formula (13) may also be used to define (without relying on any geometric background) the trigonometric functions from the definition (11) of the exponential function. Such approach (e.g. in Rudin’s book “Real and complex analysis”) seems to be more self-contained.
[A comment to this effect has now been added, thanks – T.]
20 September, 2016 at 6:35 am
Anonymous
Minor typo: the second instance of “every element” in the text reads as “every element C”. Should it be “every element of C”?
[Corrected, thanks – T.]
21 September, 2016 at 1:24 am
Rodrigue
In exercise (11), shouldn’t it be , with k ranging from 0 to
, with k ranging from 0 to 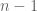 instead of starting at 1?
instead of starting at 1?
[Corrected, thanks – T.]
22 September, 2016 at 2:48 am
Anonymous
According to Wikipedia, it seems that complex numbers were first introduced and used (in the 16th century) by Cardano (who called them “fictitious”) to solve cubic equations.
22 September, 2016 at 1:45 pm
Ravi A. Bajaj
I am strongly in favor of the hierarchy of numbers outlined here, with the first passage being additivity, the second being multiplicativity, the third being metricity, and the fourth being algebra. (One reason I like it is because, though I may be at risk of abusing the context of your words, in previous posts about prime numbers you alluded to “non-multiplicative” aspects of the theory so I appreciate the sense of there being a ladder toward those aspects that manifests in the construction of the numbers themselves.)
22 September, 2016 at 7:48 pm
Anonymous
Sign error at remark 5, division formula, inside last term.
22 September, 2016 at 11:57 pm
Harsh Kumar
You use the term tangent vectors of the Argand plane in the introduction. Basically here:
“Another important geometric feature of the Argand plane is the angle between two tangent vectors to a point in the plane. ”
Could you explain what you mean by that in a little more depth. I understand from the context that you mean the angle between two complex vectors, but how are those the tangent vectors?
23 September, 2016 at 12:21 pm
Terence Tao
Formally, a tangent vector to a point in any manifold
in any manifold  is the derivative at
is the derivative at  of any differentiable curve in
of any differentiable curve in  that passes through
that passes through 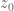 ; geometrically one thinks of such a vector as a little arrow based at
; geometrically one thinks of such a vector as a little arrow based at 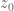 . In the case of a flat space such as the complex numbers
. In the case of a flat space such as the complex numbers  , the tangent space
, the tangent space  of the complex plane at
of the complex plane at 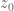 can be identified with
can be identified with  just by translating such a vector to the origin. But from a geometric point of view, one can of course take angles from any base point
just by translating such a vector to the origin. But from a geometric point of view, one can of course take angles from any base point 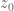 , not just the origin, so it is slightly more appropriate to think of vectors here as tangent vectors from some base point rather than just elements of
, not just the origin, so it is slightly more appropriate to think of vectors here as tangent vectors from some base point rather than just elements of 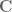 . (This also makes things easier conceptually when one considers conformal geometry of non-flat spaces, such as the Riemann sphere.)
. (This also makes things easier conceptually when one considers conformal geometry of non-flat spaces, such as the Riemann sphere.)
25 September, 2016 at 5:41 am
JDM
“Manifolds are a bit like pornography: hard to define, but you know one when you see one.”
24 September, 2016 at 10:21 pm
Anonymous
Still not fixed – maybe this was missed – there is a sign error at the division formula at remark 6, most right term,
for example it gives 1/i=+i
please check.
[Corrected, thanks – T.]
29 September, 2016 at 1:06 pm
Colin Backhurst
Really enjoying this series of notes
A few typos:
1. In remark 12 the translation for subtraction should be to 0 (like it is for addition) rather than 1 (like it is for multiplication and division)
2. Two lines above your (19) when extending cosh to be C->C you have cosh(x) where it should be cosh(z).
3. In exercise 14 (iii)”given an example” should be “give an example”
[Corrected, thanks – T.]
9 October, 2016 at 10:11 am
jsevillamol
Wonderful notes!
One small typo: when defining exponentiation, it should be $z^0=1$ instead of $z^0 = 0$.
[Corrected, thanks – T.]
16 October, 2016 at 12:49 pm
Khang
When I tried to construct the real numbers by metric completion, to avoid circularity, I used a lite version of metric topology on Q based on just rational-valued distance (concepts like delta-epsilon limits, closed sets, open sets, Cauchy sequences are still equivalent), then I defined a real as an equivalence class of Cauchy sequences in Q, a positive sequence as a sequence with a strictly positive rational lower bound (this makes the reals totally ordered) etc. Then I upgraded the metric to real-valued distance to prove the reals are complete. Is that okay or is there something I’m missing?
[Yes, that works; I adopt a similar approach for instance in my own analysis textbook. The circularity here is minor and relatively easy to circumvent, but at the cost of elegance. -T.]
27 December, 2016 at 8:20 am
Jacob
Great notes! I really appreciate all the connections that are drawn to other parts of mathematics.
Two minor typos I noticed:
1. In the line expressing the multiplicativity of complex conjugation there should be a whitespace command (e.g. “\,”) between the symbols on the right hand side.
2. One or more words are missing in the paragraph that begins “From the triangle inequality (3) and the multiplicativity (4) we see that the addition operation […]”
[Corrected, thanks – T.]
9 February, 2017 at 12:13 pm
Anonymous
Typo in
… to denote the assertion that {S} is the limit of the partial sums {\sum_{n=0}^\infty}.
[Corrected, thanks – T.]
9 February, 2017 at 12:27 pm
Anonymous
To avoid circular argument, what definition for the sine and cosine functions should one use in (8)?
9 February, 2017 at 10:32 pm
Terence Tao
One can use any definition not involving the complex numbers from which one can deduce the usual laws of trigonometry. For instance, the (real) power series definition would suffice, and is perhaps the fastest rigorous route, if the least well motivated. Alternatively, one can observe that the Argand plane obeys a modern axiom system of Euclidean geometry (e.g. the Hilbert axioms), develop notions of angle and length, and rigorously define trigonometric functions using the usual geometric definitions. One could also define the trigonometric functions by solving the harmonic oscillator ODE.
9 February, 2017 at 12:40 pm
Anonymous
… noting from (4) that the absolute convergence of the real exponential {\exp(x)} for any {x \in {\bf R}} implies the absolute convergence of the complex exponential for any {z \in {\bf C}}.
Should (4) be (7)?
[No: the point is that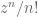 has a magnitude of
has a magnitude of  . -T]
. -T]
5 June, 2017 at 10:04 am
Five-Value Theorem of Nevanlinna – Elmar Klausmeier's Weblog
[…] 246A, Notes 0: the complex numbers […]
7 February, 2018 at 4:47 pm
Nathan Benedetto Proenca
I am having trouble with exercise 14 (ii).
I arrived at the fact that I need the subgroup to be a subset of the unit circle,
and was able to prove that its $ latex C_n$ when 1 is not a limit point.
However, I am unable to conclude that it is the whole unit circle when 1 is a limit point. I was trying to show that I can have any number of the form $ latex e^{iq}$, with $ latex q \in \mathbb{Q}$, and then to use the fact that the subgroup is closed to finish the proof. However, I am not able to show that I have every $ latex e^{i/n}$ for $ latex n \in \Naturals$ from the fact that 1 is a limit point
8 February, 2018 at 12:02 am
Terence Tao
You don’t need to have small rational angles to approximate an arbitrary element of the unit circle; small irrational angles will also work equally well.
8 February, 2018 at 10:04 am
Nathan Benedetto Proenca
Got it. Thank you very much
12 April, 2020 at 6:40 am
Atom
Prof. Terry.
I’m looking forward to studying complex analysis from these notes of yours. Can you please reassure if there are any prerequisites for these. I’ve done (more than) half of your Analysis I now, and have previously done Axler’s Linear Algebra Done Right, apart from which I’ve had no other significant exposure to abstract algebra.
Will I be losing anything what’s in your notes with only this much background?
3 October, 2020 at 5:37 pm
savitha muthanna
Prof Tao,
I have a couple of questions on Notes 0,covered in the lecture on Friday(I dont have a deep background in abstract algebra) :
1. ” The only ideal we will need to consider here is the
principal ideal: $:= {(\rom{x}^2+1)P(\rom{x}): P(\rom{x}) \in R[\rom{x}]}}$. My question is, is the ideal, generated by $$, the ‘root’ of $(\rom{x}^2 +1)$ commuted by the elements of $P(\rom{x}) $ belonging to $R(\rom{x})$? I am trying to understand the notation?
2. “If we define $i \to C$ to be the coset i:= \rom{x}+,\rom{x}^2+1},then it is clearfrom construction that $i^2+1=0$”
How is $i=x+$ ??? In fact in the lecture, you said, $P(\rom{x} + = P(\rom{x}+{\rom{x}^2+1>)=P(i)$. I din’t understand that. Consequently I don’t see how $i+1$ amounts to $\rom{x}^2+1$ or $i^2$ to $\rom{x}^2$ either.
3. I din’t completely understand how we arrived at the fact that z is invertible from finite dimensionality. I understood that C is 2 dimensional vector space. What is w in your notes? Why is this map injective? Also why is it surjective? ( I know the rank-nullity theorem).
Thank you,
4 October, 2020 at 8:20 am
Anonymous
Hope you don’t mind I make a few comments here.
1. In the definition,
the RHS is a “subset” of![{\bf R}[\mathrm{x}]](https://s0.wp.com/latex.php?latex=%7B%5Cbf+R%7D%5B%5Cmathrm%7Bx%7D%5D&bg=ffffff&fg=545454&s=0&c=20201002) . No fancy notation/meaning here. (This subset has the structure of an ideal of
. No fancy notation/meaning here. (This subset has the structure of an ideal of ![{\bf R}[\mathrm{x}]](https://s0.wp.com/latex.php?latex=%7B%5Cbf+R%7D%5B%5Cmathrm%7Bx%7D%5D&bg=ffffff&fg=545454&s=0&c=20201002) )
)
This the “quotient ring” approach rather than the “adjoining a new element” approach for defining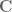 . See Remark 2.
. See Remark 2.
2. If we define to be the coset
to be the coset
then it is clear from construction that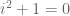 .
.
One has because we are defining the symbol
because we are defining the symbol  to be so. In order to understand the logic here, one should throw away what one assumes he knows about “complex numbers”: until this point, there is no
to be so. In order to understand the logic here, one should throw away what one assumes he knows about “complex numbers”: until this point, there is no  in the world and the excerpt above is what this symbol means. Whenever one sees
in the world and the excerpt above is what this symbol means. Whenever one sees  following this definition, one should automatically replace it with the coset
following this definition, one should automatically replace it with the coset  .
.
3. For any non-zero , the multiplication map
, the multiplication map  is an
is an  -linear map from this finite-dimensional vector space to itself.
-linear map from this finite-dimensional vector space to itself.
The multiplication map is defined on . So the variable
. So the variable 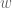 takes values in
takes values in 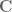 , which is the “domain” of the multiplication map. “Why is this map injective?” Because the kernel of this linear map is
, which is the “domain” of the multiplication map. “Why is this map injective?” Because the kernel of this linear map is 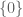 . Now you can apply the rank-nullity theorem you know to conclude that it must be subjective as well.
. Now you can apply the rank-nullity theorem you know to conclude that it must be subjective as well.
4 October, 2020 at 4:25 pm
Anonymous
1) if how is
how is 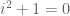 ?
? ? It would be zero if $w$ has a zero kernel. But that is not stated.
? It would be zero if $w$ has a zero kernel. But that is not stated.
3) For 3, why is the kernel map
4 October, 2020 at 5:41 pm
Terence Tao
1): use the laws of addition and multiplication in the quotient ring![{\mathbb R}[x]/\langle x^2+1 \rangle](https://s0.wp.com/latex.php?latex=%7B%5Cmathbb+R%7D%5Bx%5D%2F%5Clangle+x%5E2%2B1+%5Crangle&bg=ffffff&fg=545454&s=0&c=20201002) , as laid out in the displays shortly before the definition of
, as laid out in the displays shortly before the definition of  .
.
3): use the fact that![{\mathbb R}[x]/\langle x^2+1 \rangle](https://s0.wp.com/latex.php?latex=%7B%5Cmathbb+R%7D%5Bx%5D%2F%5Clangle+x%5E2%2B1+%5Crangle&bg=ffffff&fg=545454&s=0&c=20201002) is an integral domain.
is an integral domain.
4 October, 2020 at 7:47 pm
Anonymous
Thank you!
3 October, 2020 at 10:58 pm
adityaguharoy
Could you please edit your comment to correct the typos in it.
5 October, 2020 at 7:30 am
Anonymous
Terry, the following note in the CCLE course page (https://ccle.ucla.edu/mod/page/view.php?id=3173126):
[Note for non-UCLA participants: only homework from enrolled UCLA students will be graded. Other participants are welcome to discuss the HW questions on the blog.]
is linking to your Fourier analysis blog posts.
[Corrected, thanks – T.]
7 October, 2020 at 10:07 am
Anonymous
Do you have a reference for the picture you drew in class for Remark 10?
7 October, 2020 at 11:39 am
Terence Tao
Szamuely’s book (cited in that remark) has some further elaboration of the analogy between etale fundamental groups and topological fundamental groups, though he may not have that precise picture. You also might find this comment of Will Sawin (in the function field setting) to be helpful, as well as the famous diagram of Mumford that is called “Mumford’s treasure map” in this web page.
7 October, 2020 at 11:04 am
Ray
Typo at: {\times: {\bf C} \rightarrow {\bf C} \rightarrow {\bf C}} for defining multiplication :)
[Corrected, thanks – T.]
7 October, 2020 at 11:07 am
Anonymous
(To be clear, it’s in the limit section right before “… thus we have the familiar limit laws”)
13 December, 2020 at 8:47 am
Anonymous
… Starting with the real numbers
Typo in the font for in
in 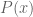 .
.
(A pedantic comment: the place holder is missing on the right—it is mentioned later in the notes that “… identifying each real number
is missing on the right—it is mentioned later in the notes that “… identifying each real number  with the degree zero polynomial
with the degree zero polynomial  )”. Otherwise the identification is already done in the definition of
)”. Otherwise the identification is already done in the definition of  .)
.)
(To be more pedantic, it is an exercise to find in the definition of the multiplicative identity that one can indeed later “identify”
that one can indeed later “identify”  with
with  and thus the real number
and thus the real number  . So it makes to write in the definition
. So it makes to write in the definition 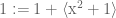 )
)
[Corrected, thanks – T.]
13 December, 2020 at 12:32 pm
Anonymous
At the beginning of section 2, to view the positive definiteness of the norm form, continuity of the norm form on the connected set
on the connected set  is used.
is used.
What “continuity argument” are you referring to in the following?
… the unit circle
[One can verify that the set of for which
for which  is orientation-preserving is non-empty, open, and closed. -T]
is orientation-preserving is non-empty, open, and closed. -T]
15 April, 2021 at 8:28 am
Ryan
Dear Terry,
I quite like your notes for the 246ABC sequence. Are there any plans to morph these into a textbook?
Warmly,
Ryan
18 April, 2021 at 10:15 pm
Terence Tao
I will teach the entire sequence again next year using this set of notes, at which point I may think about converting them to a text.
4 May, 2021 at 8:37 am
Anonymous
Dear Prof. Tao:
If classes continue to be online this coming fall, could you teach real analysis, or probability, or number theory other than complex analysis? Lots of students will benefit from your teaching.
27 September, 2021 at 9:00 am
246A, Notes 1: complex differentiation | What's new
[…] set of notes: Notes 0. Next set of notes: Notes […]
9 January, 2022 at 10:45 pm
Anonymous
Why is the closure of the reals (the complex numbers)is only twice as big, but the closure of other fields, i.e. closure of p-adiac field, and closure of the rationals are much bigger, both of infinite degree? What do you mean by infinite degree? Is the degree of complex numbers 2?
10 January, 2022 at 12:50 am
Aditya Guha Roy
The key intuition lies in observing that we need only a single element (or square root of any other negative real number) to be adjoined to
(or square root of any other negative real number) to be adjoined to 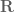 for forming the complex numbers
for forming the complex numbers  .
.
20 January, 2022 at 5:02 pm
Terence Tao
The degree of a field extension is the dimension of the extension as a vector space over the base field.
For me, one reason why the algebraic closure of the reals is only of degree 2 is that the reals are already pretty close to being algebraically closed by virtue of the intermediate value theorem, which easily implies that any polynomial of odd degree over the reals has a real root. Since the reals are already to find roots for half of the available degrees, it’s not so surprising that the algebraic completion has degree 2 as well. My intuition for the p-adics is not as good, but certainly as a bare minimum one needs to adjoin all the roots of p to the p-adics to even have a chance of being algebraically closed, which is already enough to demonstrate that the algebraic closure has infinite degree.
10 January, 2022 at 10:44 am
Anonymous
When we say dimension of a field, we usually mean dimension of the field as a vector space over another field, e.g , and
, and  . If the dimension as a vector space is not finite, we say it is infinite.
. If the dimension as a vector space is not finite, we say it is infinite.