Previous set of notes: Notes 0. Next set of notes: Notes 2.
At the core of almost any undergraduate real analysis course are the concepts of differentiation and integration, with these two basic operations being tied together by the fundamental theorem of calculus (and its higher dimensional generalisations, such as Stokes’ theorem). Similarly, the notion of the complex derivative and the complex line integral (that is to say, the contour integral) lie at the core of any introductory complex analysis course. Once again, they are tied to each other by the fundamental theorem of calculus; but in the complex case there is a further variant of the fundamental theorem, namely Cauchy’s theorem, which endows complex differentiable functions with many important and surprising properties that are often not shared by their real differentiable counterparts. We will give complex differentiable functions another name to emphasise this extra structure, by referring to such functions as holomorphic functions. (This term is also useful to distinguish these functions from the slightly less well-behaved meromorphic functions, which we will discuss in later notes.)
In this set of notes we will focus solely on the concept of complex differentiation, deferring the discussion of contour integration to the next set of notes. To begin with, the theory of complex differentiation will greatly resemble the theory of real differentiation; the definitions look almost identical, and well known laws of differential calculus such as the product rule, quotient rule, and chain rule carry over verbatim to the complex setting, and the theory of complex power series is similarly almost identical to the theory of real power series. However, when one compares the “one-dimensional” differentiation theory of the complex numbers with the “two-dimensional” differentiation theory of two real variables, we find that the dimensional discrepancy forces complex differentiable functions to obey a real-variable constraint, namely the Cauchy-Riemann equations. These equations make complex differentiable functions substantially more “rigid” than their real-variable counterparts; they imply for instance that the imaginary part of a complex differentiable function is essentially determined (up to constants) by the real part, and vice versa. Furthermore, even when considered separately, the real and imaginary components of complex differentiable functions are forced to obey the strong constraint of being harmonic. In later notes we will see these constraints manifest themselves in integral form, particularly through Cauchy’s theorem and the closely related Cauchy integral formula.
Despite all the constraints that holomorphic functions have to obey, a surprisingly large number of the functions of a complex variable that one actually encounters in applications turn out to be holomorphic. For instance, any polynomial with complex coefficients will be holomorphic, as will the complex exponential
. From this and the laws of differential calculus one can then generate many further holomorphic functions. Also, as we will show presently, complex power series will automatically be holomorphic inside their disk of convergence. On the other hand, there are certainly basic complex functions of interest that are not holomorphic, such as the complex conjugation function
, the absolute value function
, or the real and imaginary part functions
. We will also encounter functions that are only holomorphic at some portions of the complex plane, but not on others; for instance, rational functions will be holomorphic except at those few points where the denominator vanishes, and are prime examples of the meromorphic functions mentioned previously. Later on we will also consider functions such as branches of the logarithm or square root, which will be holomorphic outside of a branch cut corresponding to the choice of branch. It is a basic but important skill in complex analysis to be able to quickly recognise which functions are holomorphic and which ones are not, as many of useful theorems available to the former (such as Cauchy’s theorem) break down spectacularly for the latter. Indeed, in my experience, one of the most common “rookie errors” that beginning complex analysis students make is the error of attempting to apply a theorem about holomorphic functions to a function that is not at all holomorphic. This stands in contrast to the situation in real analysis, in which one can often obtain correct conclusions by formally applying the laws of differential or integral calculus to functions that might not actually be differentiable or integrable in a classical sense. (This latter phenomenon, by the way, can be largely explained using the theory of distributions, as covered for instance in this previous post, but this is beyond the scope of the current course.)
Remark 1 In this set of notes it will be convenient to impose some unnecessarily generous regularity hypotheses (e.g. continuous second differentiability) on the holomorphic functions one is studying in order to make the proofs simpler. In later notes, we will discover that these hypotheses are in fact redundant, due to the phenomenon of elliptic regularity that ensures that holomorphic functions are automatically smooth.
— 1. Complex differentiation and power series —
Recall in real analysis that if is a function defined on some subset
of the real line
, and
is an interior point of
(that is to say,
contains an interval of the form
for some
), then we say that
is differentiable at
if the limit
exists (note we have to exclude from the possible values of
to avoid division by zero. If
is differentiable at
, we denote the above limit as
or
, and refer to this as the derivative of
at
. If
is open (that is to say, every element of
is an interior point), and
is differentiable at every point of
, then we say that
is differentiable on
, and call
the derivative of
. (One can also define differentiability at non-interior points if they are not isolated, but for simplicity we will restrict attention to interior derivatives only.)
We can adapt this definition to the complex setting without any difficulty:
Definition 2 (Complex differentiability) Let
be a subset of the complex numbers
, and let
be a function. If
is an interior point of
(that is to say,
contains a disk
for some
), we say that
is complex differentiable at
if the limit
exists, in which case we denote this limit as
,
, or
, and refer to this as the complex derivative of
at
. If
is open (that is to say, every point in
is an interior point), and
is complex differentiable at every point at
, we say that
is complex differentiable on
, or holomorphic on
.
In terms of epsilons and deltas: is complex differentiable at
with derivative
if and only if, for every
, there exists
such that
whenever
is such that
. Another way of writing this is that we have an approximate linearisation
as approaches
, where
denotes a quantity of the form
for
in a neighbourhood of
, where
goes to zero as
goes to
. Making the change of variables
, one can also write the derivative
in the familiar form
where is the translation of
by
.
If is differentiable at
, then from the limit laws we see that
and hence
that is to say that is continuous at
. In particular, holomorphic functions are automatically continuous. (Later on we will see that they are in fact far more regular than this, being smooth and even analytic.)
It is usually quite tedious to verify complex differentiability of a function, and to compute its derivative, from first principles. We will give just one example of this:
Proposition 3 Let
be a non-negative integer. Then the function
is holomorphic on the entire complex plane
, with derivative
(with the convention that
is zero when
).
Proof: This is clear for , so suppose
. We need to show that for any complex number
, that
But we have the geometric series identity
which is valid (in any field) whenever , as can be seen either by induction or by multiplying both sides by
and cancelling the telescoping series on the right-hand side. The claim then follows from the usual limit laws.
Fortunately, we have the familiar laws of differential calculus, that allow us to more quickly establish the differentiability of functions if they arise as various combinations of functions that are already known to be differentiable, and to compute the derivative:
Exercise 4 (Laws of differentiation) Let
be an open subset of
, let
be a point in
, and let
be functions that are complex differentiable at
.
- (i) (Linearity) Show that
is complex differentiable at
, with derivative
. For any constant
, show that
is differentiable at
, with derivative
.
- (ii) (Product rule) Show that
is complex differentiable at
, with derivative
.
- (iii) (Quotient rule) If
is non-zero, show that
(which is defined in a neighbourhood of
, by continuity) is complex differentiable at
, with derivative
.
- (iv) (Chain rule) If
is a neighbourhood of
, and
is a function that is complex differentiable at
, show that the composition
(which is defined in a neighbourhood of
) is complex differentiable at
, with derivative
(Hint: take your favourite proof of the real-variable version of these facts and adapt them to the complex setting.)
One could also state and prove a complex-variable form of the inverse function theorem here, but the proof of that statement is a bit more complicated than the ones in the above exercise, so we defer it until later in the course when it becomes needed.
If a function is holomorphic on the entire complex plane, we call it an entire function; clearly such functions remain holomorphic when restricted to any open subset
of the complex plane. Thus for instance Proposition 3 tells us that the functions
are entire, and from linearity we then see that any complex polynomial
will be an entire function, with derivative given by the familiar formula
A function of the form , where
are polynomials with
not identically zero, is called a rational function, being to polynomials as rational numbers are to integers. Such a rational function is well defined as long as
is not zero. From the factor theorem (which works over any field, and in particular over the complex numbers) we know that the number of zeroes of
is finite, being bounded by the degree of
(of course we will be able to say something stronger once we have the fundamental theorem of algebra). Because of these singularities, rational functions are rarely entire; but from the quotient rule we do at least see that
is complex differentiable wherever the denominator is non-zero. Such functions are prime examples of meromorphic functions, which we will discuss later in the course.
Exercise 5 (Gauss-Lucas theorem) Let
be a complex polynomial that is factored as
for some non-zero constant
and roots
(not necessarily distinct) with
.
- (i) Suppose that
all lie in the upper half-plane
. Show that any root of the derivative
also lies in the upper half-plane. (Hint: use the product rule to decompose the log-derivative
into partial fractions, and then investigate the sign of the imaginary part of this log-derivative for
outside the upper half-plane.)
- (ii) Show that all the roots of
lie in the convex hull of the set
of roots of
, that is to say the smallest convex polygon that contains
.
Now we discuss power series, which are infinite degree variants of polynomials, and which turn out to inherit many of the algebraic and analytic properties of such polynomials, at least if one stays within the disk of convergence.
Definition 6 (Power series) Let
be a complex number. A formal power series with complex coefficients around the point
is a formal series of the form
for some complex numbers
, with
an indeterminate.
One can attempt to evaluate a formal power series at a given complex number
by replacing the formal indeterminate
with the complex number
. This may or may not produce a convergent (or absolutely convergent) series, depending on where
is; for instance, the power series
is always absolutely convergent at
, but the geometric power series
fails to be even conditionally convergent whenever
(since the summands do not go to zero). As it turns out, the region of convergence is always essentially a disk, the size of which depends on how rapidly the coefficients
decay (or how slowly they grow):
Proposition 7 (Convergence of power series) Let
be a formal power series, and define the radius of convergence
of the series to be the quantity
with the convention that
is infinite if
. (Note that
is allowed to be zero or infinite.) Then the formal power series is absolutely convergent for any
in the disk
(known as the disk of convergence), and is divergent (i.e., not convergent) for any
in the exterior region
.
Proof: The proof is nearly identical to the analogous result for real power series. First suppose that is a complex number with
(this of course implies that
is finite). Then by (3), we have
for infinitely many
, which after some rearranging implies that
for infinitely many
. In particular, the sequence
does not go to zero as
, which implies that
is divergent.
Now suppose that is a complex number with
(this of course implies that
is non-zero). Choose a real number
with
, then by (3), we have
for all sufficiently large
, which after some rearranging implies that
for all sufficiently large . Since the geometric series
is absolutely convergent, this implies that
is absolutely convergent also, as required.
Remark 8 Note that this proposition does not say what happens on the boundary
of this disk (assuming for sake of discussion that the radius of convergence
is finite and non-zero). The behaviour of power series on and near the boundary of the disk of convergence is in fact remarkably subtle; see for instance Example 11 below.
The above proposition gives a “root test” formula for the radius of convergence. The following “ratio test” variant gives convenient lower and upper bounds for the radius of convergence which suffices in many applications:
Exercise 9 (Ratio test) If
is a formal power series with the
non-zero for all sufficiently large
, show that the radius of convergence
of the series obeys the lower bound
In particular, if the limit
exists, then it is equal to
. Give examples to show that strict inequality can hold in either of the bounds in (4). (For an extra challenge, provide an example where both bounds are simultaneously strict.)
If a formal power series has a positive radius of convergence, then it defines a function
in the disk of convergence by setting
We refer to such a function as a power series, and refer to as the radius of convergence of that power series. (Strictly speaking, a formal power series and a power series are different concepts, but there is little actual harm in conflating them together in practice, because of the uniqueness property established in Exercise 17 below.)
Example 10 The formal power series
has a zero radius of convergence, thanks to the ratio test, and so only converges at
. Conversely, the exponential formal power series
has an infinite radius of convergence (thanks to the ratio test), and converges of course to
when evaluated at any complex number
.
Example 11 (Geometric series) The formal power series
has radius of convergence
. If
lies in the disk of convergence
, then we have
and thus after some algebra we obtain the geometric series formula
as long as
is inside the disk
. The function
does not extend continuously to the boundary point
of the disk, but does extend continuously (and even smoothly) to the rest of the boundary, and is in fact holomorphic on the remainder
of the complex plane. However, the geometric series
diverges at every single point of this boundary (when
, the coefficients
of the series do not converge to zero), and of course definitely diverge outside of the disk as well. Thus we see that the function that a power series converges to can extend well beyond the disk of convergence, which thus may only capture a portion of the domain of definition of that function. For instance, if one formally applies (5) with, say,
, one ends up with the apparent identity
This identity does not make sense if one interprets infinite series in the classical fashion, as the series
is definitely divergent. However, by formally extending identities such as (5) beyond their disk of convergence, we can generalise the notion of summation of infinite series to assign meaningful values to such series even if they do not converge in the classical sense. This leads to generalised summation methods such as zeta function regularisation, which are discussed in this previous blog post. However, we will not use such generalised interpretations of summation very much in this course.
Exercise 12 For any complex numbers
, show that the formal power series
has radius of convergence
(with the convention that this is infinite for
), and is equal to the function
inside the disk of convergence.
Exercise 13 For any positive integer
, show that the formal power series
has radius of convergence
, and converges to the function
in the disk
. Here of course
is the usual binomial coefficient.
We have seen above that power series can be well behaved as one approaches the boundary of the disk of convergence, while being divergent at the boundary. However, the converse scenario, in which the power series converges at the boundary but does not behave well as one approaches the boundary, does not occur:
Exercise 14
(i) (Summation by parts formula) Let be a finite sequence of complex numbers, and let
be the partial sums for
. Show that for any complex numbers
, that
(ii) Let be a sequence of complex numbers such that
is convergent (not necessarily absolutely) to zero. Show that for any
, the series
is absolutely convergent, and
(Hint: use summation by parts and a limiting argument to express
in terms of the partial sums
.)
(iii) (Abel’s theorem) Let be a power series with a finite positive radius of convergence
, and let
be a point on the boundary of the disk of convergence at which the series
converges (not necessarily absolutely). Show that
. (Hint: use various translations and rotations to reduce to the case considered in (ii).)
As a general rule of thumb, as long as one is inside the disk of convergence, power series behave very similarly to polynomials. In particular, we can generalise the differentiation formula (2) to such power series:
Theorem 15 Let
be a power series with a positive radius of convergence
. Then
is holomorphic on the disk of convergence
, and the derivative
is given by the power series
that has the same radius of convergence
as
.
Proof: From (3), the standard limit and the usual limit laws, it is easy to see that the power series
has the same radius of convergence
as
. To show that this series is actually the derivative of
, we use first principles. If
lies in the disk of convergence, we consider the Newton quotient
for . Expanding out the absolutely convergent series
and
, we can write
The ratio vanishes for
, and for
it is equal to
as in the proof of Proposition 3. Thus
As approaches
, each summand
converges to
. This almost proves the desired limiting formula
but we need to justify the interchange of a sum and limit. Fortunately we have a standard tool for this, namely the Weierstrass -test (which works for complex-valued functions exactly as it does for real-valued functions; one could also use the dominated convergence theorem here). It will be convenient to select two real numbers
with
. Clearly, for
close enough to
, we have
. By the triangle inequality we then have
On the other hand, from (3) we know that for sufficiently large
, hence
for sufficiently large
. From the ratio test we know that the series
is absolutely convergent, hence the series
is also. Thus, for
sufficiently close to
, the summands
are uniformly dominated by an absolutely summable sequence of numbers
. Applying the Weierstrass
-test (or dominated convergence theorem), we obtain the claim.
Exercise 16 Prove the above theorem directly using epsilon and delta type arguments, rather than invoking the
-test or the dominated convergence theorem.
We remark that the above theorem is a little easier to prove once we have the complex version of the fundamental theorem of calculus, but this will have to wait until the next set of notes, where we will also prove a remarkable converse to the above theorem, in that any holomorphic function can be expanded as a power series around any point in its domain.
A convenient feature of power series is the ability to equate coefficients: if two power series around the same point agree, then their coefficients must also agree. More precisely, we have:
Exercise 17 (Taylor expansion and uniqueness of power series) Let
be a power series with a positive radius of convergence. Show that
, where
denotes the
complex derivative of
. In particular, if
is another power series around
with a positive radius of convergence which agrees with
on some neighbourhood
of
(thus,
for all
), show that the coefficients of
and
are identical, that is to say that
for all
.
Of course, one can no longer compare coefficients so easily if the power series are based around two different points. For instance, from Exercise 11 we see that the geometric series and
both converge to the same function
on the unit disk
, but have differing coefficients. The precise relation between the coefficients of power series of the same function is given as follows:
Exercise 18 (Changing the origin of a power series) Let
be a power series with a positive radius of convergence
. Let
be an element of the disk of convergence
. Show that the formal power series
, where
has radius of convergence at least
, and converges to
on the disk
. Here of course
is the usual binomial coefficient.
Theorem 15 gives us a rich supply of complex differentiable functions, particularly when combined with Exercise 4. For instance, the complex exponential function
has an infinite radius of convergence, and so is entire, and is its own derivative:
This makes the complex trigonometric functions
entire as well, and from the chain rule we recover the familiar formulae
Of course, one can combine these functions together in many ways to create countless other complex differentiable functions with explicitly computable derivatives, e.g. is an entire function with derivative
, the tangent function
is holomorphic outside of the discrete set
with derivative
, and so forth.
Exercise 19 (Multiplication of power series) Let
and
be power series that both have radius of convergence at least
. Show that on the disk
, we have
where the right-hand side is another power series of radius of convergence at least
, with coefficients
given as the convolution
of the sequences
and
.
— 2. The Cauchy-Riemann equations —
Thus far, the theory of complex differentiation closely resembles the analogous theory of real differentiation that one sees in an introductory real analysis class. But now we take advantage of the Argand plane representation of to view a function
of one complex variable as a function
of two real variables. This gives rise to some further notions of differentiation. Indeed, if
is a function defined on an open subset of
, and
is a point in
, then in addition to the complex derivative
already discussed, we can also define (if they exist) the partial derivatives
and
these will be complex numbers if the limits on the right-hand side exist. There is also (if it exists) the gradient (or Fréchet derivative) , defined as the vector
with the property that
where is the Euclidean norm of
.
These notions of derivative are of course closely related to each other. If a function is Fréchet differentiable at
, in the sense that the gradient
exists, then on specialising the limit in (7) to vectors
of the form
or
we see that
and
leading to the familiar formula
for the gradient of a function
that is Fréchet differentiable at
. We caution however that it is possible for the partial derivatives
of a function to exist without the function being Fréchet differentiable, in which case the formula (8) is of course not valid. (A typical example is the function
defined by setting
for
, with
; this function has both partial derivatives
existing at
, but
is not differentiable here.) On the other hand, if the partial derivatives
exist everywhere on
and are additionally known to be continuous, then the fundamental theorem of calculus gives the identity
for and
sufficiently small (with the convention that
if
), and from this it is not difficult to see that
is then Fréchet differentiable everywhere on
.
Similarly, if is complex differentiable at
, then by specialising the limit (6) to variables
of the form
or
for some non-zero real
near zero, we see that
and
leading in particular to the Cauchy-Riemann equations
that must be satisfied in order for to be complex differentiable. More generally, from (6) we see that if
is complex differentiable at
, then
which on comparison with (7) shows that is also Fréchet differentiable with
Finally, if is Fréchet differentiable at
and one has the Cauchy-Riemann equations (9), then from (7) we have
which after making the substitution gives
which on comparison with (6) shows that is complex differentiable with
We summarise the above discussion as follows:
Proposition 20 (Differentiability and the Cauchy-Riemann equations) Let
be an open subset of
, let
be a function, and let
be an element of
.
- (i) If
is complex differentiable at
, then it is also Fréchet differentiable at
, with
In particular, the Cauchy-Riemann equations (9) hold at
.
- (ii) Conversely, if
is Fréchet differentiable at
and obeys the Cauchy-Riemann equations at
, then
is complex differentiable at
.
Remark 21 From part (ii) of the above proposition we see that if
is Fréchet differentiable on
and obeys the Cauchy-Riemann equations on
, then it is holomorphic on
. One can ask whether the requirement of Fréchet differentiability can be weakened. It cannot be omitted entirely; one can show, for instance, that the function
defined by
for non-zero
and
obeys the Cauchy-Riemann equations at every point
, but is not complex differentiable (or even continuous) at the origin. But there is a somewhat difficult theorem of Looman and Menchoff that asserts that if
is continuous on
and obeys the Cauchy-Riemann equations on
, then it is holomorphic. We will not prove or use this theorem in this course; generally in modern applications, when one wants to weaken the regularity hypotheses of a theorem involving classical differentiation, the best way to do so is to replace the notion of a classical derivative with that of a weak derivative, rather than insist on computing derivatives in the classical pointwise sense. See this blog post for more discussion.
Combining part (i) of the above proposition with Theorem 15, we also conclude as a corollary that any power series will be smooth inside its disk of convergence, in the sense all partial derivatives to all orders of this power series exist.
Remark 22 From the geometric perspective, one can interpret complex differentiability at a point
as a requirement that a map
is conformal and orientation-preserving at
, at least in the non-degenerate case when
is non-zero. In more detail: suppose that
is a map that is complex differentiable at some point
with
. Let
be a differentiable curve with
; we view this as the trajectory of some particle which passes through
at time
. The derivative
(defined in the usual manner by limits of Newton quotients) can then be viewed as the velocity of the particle as it passes through
. The map
takes this particle to a new particle parameterised by the curve
; at time
, this new particle passes through
, and by the chain rule we see that the velocity of the new particle at this time is given by
Thus, if we write
in polar coordinates as
, the map
transforms the velocity of the particle by multiplying the speed by a factor of
and rotating the direction of travel counter-clockwise by
. In particular, we consider two differentiable trajectories
both passing through
at time
(with non-zero speeds), then the map
preserves the angle between the two velocity vectors
, as well as their orientation (e.g. if
is counterclockwise to
, then
is counterclockwise to
. This is in contrast to, for instance, shear transformations such as
, which preserve orientation but not angle, or the complex conjugation map
, which preserve angle but not orientation. The same preservation of angle is present for real differentiable functions
on an interval
, but is much less impressive in that case since the only angles possible between two vectors on the real line are
and
; it is the geometric two-dimensionality of the complex plane that makes conformality a much stronger and more “rigid” property for complex differentiable functions.
One consequence of the first component of Proposition 20(i) is that the complex notion of differentiation and the real notion of differentiation are compatible with each other. More precisely, if
is holomorphic and
is the restriction of
to the real line, then the real derivative
of
exists and is equal to the restriction of the complex derivative
to the real line. For instance, since
for a complex variable
, we also have
for a real variable
. For similar reasons, it will be a safe “abuse of notation” to use the notation
both to refer to the complex derivative of a function
, and also the real derivative of the restriction of that function to the real line.
If one breaks up a complex function into real and imaginary parts
for some
, then on taking real and imaginary parts one can express the Cauchy-Riemann equations as a system
of two partial differential equations for two functions . This gives a quick way to test if various functions are differentiable. Consider for instance the conjugation function
. In this case,
and
. These functions, being polynomial in
, is certainly Fréchet differentiable everywhere; the equation (11) is always satisfied, but the equation (10) is never satisfied. As such, the conjugation function is never complex differentiable. Similarly for the real part function
, the imaginary part function
, or the absolute value function
. The function
has real part
and imaginary part
; one easily checks that the system (10), (11) is only satisfied when
, so this function is only complex differentiable at the origin. In particular, it is not holomorphic on any non-empty open set.
The general rule of thumb that one should take away from these examples is that complex functions that are constructed purely out of “good” functions such as polynomials, the complex exponential, complex trigonometric functions, or other convergent power series are likely to be holomorphic, whereas functions that involve “bad” functions such as complex conjugation, the real and imaginary part, or the absolute value, are unlikely to be holomorphic.
Exercise 23 (Wirtinger derivatives) Let
be an open subset of
, and let
be a Fréchet differentiable function. Define the Wirtinger derivatives
,
by the formulae
- (i) Show that
is holomorphic on
if and only if the Wirtinger derivative
vanishes identically on
.
- (ii) If
is given by a polynomial
in both
and
for some complex coefficients
and some natural number
, show that
and
(Hint: first establish a Leibniz rule for Wirtinger derivatives.) Conclude in particular that
is holomorphic if and only if
vanishes whenever
(i.e.
does not contain any terms that involve
).
- (iii) If
is a point in
, show that one has the Taylor expansion
as
, where
denotes a quantity of the form
, where
goes to zero as
goes to
(compare with (1)). Conversely, show that this property determines the numbers
and
uniquely (and thus can be used as an alternate definition of the Wirtinger derivatives).
Remark 24 Any polynomial
in the real and imaginary parts
of
can be rewritten as a polynomial in
and
as per (17), using the usual identities
for
. Thus such a non-holomorphic polynomial of one complex variable
can be viewed as the restriction of a holomorphic polynomial
of two complex variables
to the anti-diagonal
, and the Wirtinger derivatives can then be interpreted as genuine (complex) partial derivatives in these two complex variables. More generally, Wirtinger derivatives are convenient tools in the subject of several complex variables, which we will not cover in this course.
The Cauchy-Riemann equations couple the real and imaginary parts of a holomorphic function to each other. But it is also possible to eliminate one of these components from the equations and obtain a constraint on just the real part
, or just the imaginary part
. Suppose for the moment that
is a holomorphic function which is twice continuously differentiable (thus the second partial derivatives
,
,
,
all exist and are continuous on
); we will show in the next set of notes that this extra hypothesis is in fact redundant. Assuming continuous second differentiability for now, we have Clairaut’s theorem
everywhere on . Similarly for the real and imaginary parts
. If we then differentiate (10) in the
direction, (11) in the
direction, and then sum, the derivatives of
cancel thanks to Clairaut’s theorem, and we obtain Laplace’s equation
which is often written more compactly as
where is the Laplacian operator
A similar argument gives ; by linearity we then also have
.
Functions for which
is continuously twice differentiable and
are known as harmonic functions: thus we have shown that (continuously twice differentiable) holomorphic functions are automatically harmonic, as are the real and imaginary parts of such functions. The converse is not true: not every harmonic function
is holomorphic. For instance, the conjugate function
is clearly harmonic on
, but not holomorphic. We will return to the precise relationship between harmonic and holomorphic functions shortly.
Harmonic functions have many remarkable properties. Since the second derivative in a given direction is a local measure of “convexity” of a function, we see from (13) that any convex behaviour of a harmonic function in one direction has to be balanced by an equal and opposite amount of concave behaviour in the orthogonal direction. A good example of a harmonic function to keep in mind is the function
which exhibits convex behavior in and concave behavior in
in exactly opposite amounts. This function is the real part of the holomorphic function
, which is of course consistent with the previous observation that the real parts of holomorphic functions are harmonic.
We will discuss harmonic functions more in later notes. For now, we record just one important property of these functions, namely the maximum principle:
Theorem 25 (Maximum principle) Let
be an open subset of
, and let
be a harmonic function. Let
be a compact subset of
, and let
be the boundary of
. Then
Informally, the maximum principle asserts that the maximum of a real-valued harmonic function on a compact set is always attained on the boundary, and similarly for the minimum. In particular, any bound on the harmonic function that one can obtain on the boundary is automatically inherited by the interior. Compare this with a non-harmonic function such as , which is bounded by
on the boundary of the compact unit disk
, but is not bounded by
on the interior of this disk.
Proof: We begin with an “almost proof” of this principle, and then repair this attempted proof so that it is an actual proof.
We will just prove (14), as (15) is proven similarly (or one can just observe that if is harmonic then so is
). Clearly we have
so the only scenario that needs to be excluded is when
Suppose that this is the case. As is continuous and
is compact,
must attain its maximum at some point
in
; from (16) we see that
must be an interior point. Since
is a local maximum of
, and
is twice differentiable, we must have
and similarly
This almost, but does not quite, contradict the harmonicity of , since it is still possible that both of these partial derivatives vanish. To get around this problem we use the trick of creating an epsilon of room, adding a tiny bit of convexity to
. Let
be a small number to be chosen later, and let
be the modified function
Since is compact, the function
is bounded on
. Thus, from (16), we see that if
is small enough we have
Arguing as before, must attain its maximum at some interior point
of
, and so we again have
and similarly
On the other hand, since is harmonic, we have
on . These facts contradict each other, and we are done.
Exercise 26 (Maximum principle for holomorphic functions) If
is a continuously twice differentiable holomorphic function on an open set
, and
is a compact subset of
, show that
(Hint: use Theorem 25 and the fact that
for any complex number
. You may find the proof of Lemma 8 in the next set of notes to be helpful as inspiration.) What happens if we replace the suprema on both sides by infima? This result is also known as the maximum modulus principle.
Exercise 27 Recall the Wirtinger derivatives defined in Exercise 23(i).
- (i) If
is twice continuously differentiable on an open subset
of
, show that
Use this to give an alternate proof that (
) holomorphic functions are harmonic.
- (ii) If
is given by a polynomial
in both
and
for some complex coefficients
and some natural number
, show that
is harmonic on
if and only if
vanishes whenever
and
are both positive (i.e.
only contains terms
or
that only involve one of
or
).
- (iii) If
is a real polynomial
in
and
for some real coefficients
and some natural number
, show that
is harmonic if and only if it is the real part of a polynomial
of one complex variable
.
We have seen that the real and imaginary parts of any holomorphic function
are harmonic functions. Conversely, let us call a harmonic function
a harmonic conjugate of another harmonic function
if
is holomorphic on
; this is equivalent by Proposition 20 to
satisfying the Cauchy-Riemann equations (10), (11). Here is a short table giving some examples of harmonic conjugates:
| |
|
|
| |
|
|
| |
|
|
| |
|
|
| |
|
|
| |
|
|
| |
|
|
(for the last example one of course has to exclude the origin from the domain ).
From Exercise 27(ii) we know that every harmonic polynomial has at least one harmonic conjugate; it is natural to ask whether the same fact is true for more general harmonic functions than polynomials. In the case that the domain is the entire complex plane, the answer is affirmative:
Proposition 28 Let
be a harmonic function. Then there exists a harmonic conjugate
of
. Furthermore, this harmonic conjugate is unique up to constants: if
are two harmonic conjugates of
, then
is a constant function.
Proof: We first prove uniqueness. If is a harmonic conjugate of
, then from the fundamental theorem of calculus, we have
and hence by the Cauchy-Riemann equations (10), (11) we have
Similarly for any other harmonic conjugate of
. It is now clear that
and
differ by a constant.
Now we prove existence. Inspired by the above calculations, we define to be the define
explicitly by the formula
From the fundamental theorem of calculus, we see that is differentiable in the
direction with
This is one of the two Cauchy-Riemann equations needed. To obtain the other one, we differentiate (18) in the variable. The fact that
is continuously twice differentiable allows one to differentiate under the integral sign (exercise!) and conclude that
As is harmonic, we have
, so by the fundamental theorem of calculus we conclude that
Thus we now have both of the Cauchy-Riemann equations (10), (11) in . Differentiating these equations again, we conclude that
is twice continuously differentiable, and hence by Proposition 20 we have
holomorphic on
, giving the claim.
The same argument would also work for some other domains than , such as rectangles
. To handle the general case, though, it becomes convenient to introduce the notion of contour integration, which we will do in the next set of notes. In some cases (specifically, when the underlying domain
fails to be simply connected), it will turn out that some harmonic functions do not have conjugates!
Exercise 29 Show that an entire function
can be real-valued on
only if it is constant.
Exercise 30 Let
be a complex number. Show that if
is an entire function such that
for all
, then
for all
.

80 comments
Comments feed for this article
23 September, 2016 at 1:16 am
g
Typo in exercise 13: you have a fraction instead of a binomial coefficient. (Either that or there’s a TeX rendering bug somewhere.)
[Corrected, thanks – T.]
23 September, 2016 at 1:34 am
Sébastien Boisgérault
Could you categorize this document as “246A — complex analysis” ?
(otherwise it won’t be listed in ).
Regards, SB.
[Done, thanks – T.]
23 September, 2016 at 4:55 am
Anonymous
In exercise 5(ii), it seems that the convex hull of the roots of is the smallest possible convex set containing the roots of
is the smallest possible convex set containing the roots of 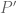 if and only if
if and only if  has multiple(!) roots on all the vertices of the convex hull of its roots.
has multiple(!) roots on all the vertices of the convex hull of its roots.
23 September, 2016 at 5:03 am
Anonymous
In the second line of definition 6, “is” is missing before “a formal”.
[Corrected, thanks – T.]
23 September, 2016 at 5:06 am
Jhon Manugal
I would hardly debate the Maximum principle as stated here and yet it has such profound consequences. I never quite see it coming. It is a bit like following a game of 3 card monte.
23 September, 2016 at 6:12 am
Anonymous
In remark 21, it seems that should be
should be 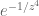 for
for 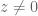 (in order to be smooth on the real and imaginary axes.)
(in order to be smooth on the real and imaginary axes.)
[Corrected, thanks – T.]
23 September, 2016 at 6:50 am
Dirk
When reading the notes, it appeared to my that the fact that holomorphic functions are so rigid can be seen also (and probably most clearly) in the formulation of complex differentiability by linearization: If we view as mapping from
as mapping from 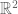 to itself, we would allow for an arbitrary linear map as derivative. However, we view
to itself, we would allow for an arbitrary linear map as derivative. However, we view  as map from
as map from 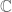 to itself and only allow for very special linear maps, namely those given by complex multiplication. This greatly restricts the class of linear maps that are allowed to use for linearization, namely to
to itself and only allow for very special linear maps, namely those given by complex multiplication. This greatly restricts the class of linear maps that are allowed to use for linearization, namely to  matrices which have constant diagonal and are skew symmetric. As far as I remember, I haven’t seen this view in any textbook – do you know any book where complex differentiability is discussed this way?
matrices which have constant diagonal and are skew symmetric. As far as I remember, I haven’t seen this view in any textbook – do you know any book where complex differentiability is discussed this way?
[Ah, I had forgotten to add a remark on precisely this; done so now. I think this is discussed for instance in Ahlfors’ book. -T.]
23 September, 2016 at 8:35 am
Anonymous
In exercise 26(ii), it seems that “whenever ” should be “whenever
” should be “whenever 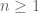 or
or 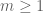 “.
“.
[Remark clarified – T.]
23 September, 2016 at 10:10 pm
Anonymous
Dear Terry,
I am a female teacher of math.Iam 32.Iam still alone.I admire and like(even I love you,but what a pity you have got married).I always care and follow you,I wonder that this september(nearly end of 2016 ),I do not still your breakththrough,while every year your name attached with great events(2013-Terry Tao and Twin primes,2014-Terry Tao and Navier Stokes,2015-Terry Tao and Erdos problem,2016-?????)
Best wishes,
Natasha,
23 September, 2016 at 11:09 pm
Anonymous
Suppose that is any(!) local coordinate system for a neighborhood of the origin in
is any(!) local coordinate system for a neighborhood of the origin in 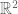 , is it possible by defining
, is it possible by defining  to develop a completely analogous theory for holomorphic and analytic functions with respect to the complex variable
to develop a completely analogous theory for holomorphic and analytic functions with respect to the complex variable 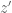 ?
?
24 September, 2016 at 9:35 am
Terence Tao
Certainly! Of course, the underlying vector space, topological, or smooth structure of may have little to do with the complex structure thus created if the local coordinate system used is nonlinear, discontinuous, or non-smooth respectively.
may have little to do with the complex structure thus created if the local coordinate system used is nonlinear, discontinuous, or non-smooth respectively.
24 September, 2016 at 12:55 pm
Anonymous
As a nice application, suppose that the new coordinates are sufficiently smooth functions of the (“reference”) coordinates
are sufficiently smooth functions of the (“reference”) coordinates  (e.g.
(e.g.  with nonsingular Jacobian matrix near the origin) and
with nonsingular Jacobian matrix near the origin) and  are also smooth functions of
are also smooth functions of 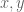 . Then to check if the complex variable $w’ = u’ + v’$ can be represented as a power series of $z’ = x’ + i y’$ near the origin, one needs only to check if
. Then to check if the complex variable $w’ = u’ + v’$ can be represented as a power series of $z’ = x’ + i y’$ near the origin, one needs only to check if  satisfy the Cauchy-Riemann equations (with respect to
satisfy the Cauchy-Riemann equations (with respect to 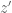 ) near the origin.
) near the origin.
24 September, 2016 at 1:04 pm
Anonymous
Correction: it should be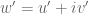
26 September, 2016 at 2:52 am
Anonymous
Remark 21 : There seems to be a missing link under “this blog post”
A bit later : “\href{harmonic conjugate}” should probably link to something as well.
[Corrected, thanks – T.]
26 September, 2016 at 5:39 pm
Steven Gubkin
I remember being frustrated by the definition of Wirtinger derivatives when I was learning this subject. Two points which might be helpful:
Any real linear map can be uniquely decomposed into a complex linear map and a complex antilinear map. When you apply this to the real linear derivative of a complex function
can be uniquely decomposed into a complex linear map and a complex antilinear map. When you apply this to the real linear derivative of a complex function  at a point
at a point  , you obtain exactly the formulas for the Wirtinger derivatives:
, you obtain exactly the formulas for the Wirtinger derivatives: 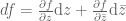 .
.
Another thing: the Wirtinger derivatives are perhaps more clearly written as
and
[Good suggestions, I have added them to the text – T.]
27 September, 2016 at 6:01 am
Anonymous
Typo in the delta-epsilon definition near beginning: should say |z – z0| < delta.
Thanks for making these notes!
[Corrected, thanks – T.]
27 September, 2016 at 10:58 am
Anonymous
It seems that in exercise 26 (and also in theorem 25), one can assume (without loss of generality) that is closed (not necessarily compact), since by appropriate bilinear transformation it can be mapped to a compact set.
is closed (not necessarily compact), since by appropriate bilinear transformation it can be mapped to a compact set.
27 September, 2016 at 11:22 am
Terence Tao
This is only true if one works in the Riemann sphere (with its attendant topological and complex structures), which is where bilinear transformations live as complex automorphisms. Otherwise there are many counterexamples, e.g. is unbounded on the upper half-plane, but is bounded on the boundary of that half-plane. (See however the Phragmen-Lindelof principle for an important partial result in this direction.)
is unbounded on the upper half-plane, but is bounded on the boundary of that half-plane. (See however the Phragmen-Lindelof principle for an important partial result in this direction.)
1 October, 2016 at 9:38 pm
Anonymous
Hello professor, for the ratio test (Ex 9), we also have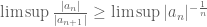 , right? Thank you for your time.
, right? Thank you for your time.
2 October, 2016 at 9:05 am
Math 246A, Notes 3: Cauchy’s theorem and its consequences | What's new
[…] this and Proposition 7 of Notes 1, we see that the radius of convergence of is indeed at least […]
9 October, 2016 at 4:13 am
Fred Lunnon
Following equn. (8) —
for “existing at {z_0}, but {f} is not differentiable here”
read “existing at {z_0 = 0}, but {f} is not differentiable here”
prop. 20, remark 21 — “Fréchet” (3 times)
[Corrected, thanks – T.]
12 October, 2016 at 2:00 pm
Anonymous
May be in Proposition 20 “ ” and “
” and “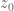 be an element of
be an element of  .” are typos and they should be “
.” are typos and they should be “ ” and “element of
” and “element of  “.
“.
[Corrected, thanks – T.]
18 October, 2016 at 9:32 pm
246A, Notes 5: conformal mapping | What's new
[…] Exercise 2 Establish Lemma 1(ii) by direct calculation, avoiding the use of holomorphic functions. (Hint: the calculations are cleanest if one uses Wirtinger derivatives, as per Exercise 27 of Notes 1.) […]
23 December, 2016 at 5:27 am
Venky
Great notes! Two typos: in the proof of Proposition 7, there is a badly formed expression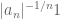 , and there is an extra
, and there is an extra  in the equation right after equation (18).
in the equation right after equation (18).
[Corrected, thanks – T.]
12 February, 2017 at 5:27 am
Anonymous
There is also (if it exists) the gradient (or Fréchet derivative) {Df(z_0) \in {\bf C}^2}, defined as the vector {(D_1 f(z_0), D_2 f(z_0)) \in {\bf C}^2} with the property that…
Should be
be 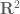 instead? I cannot make sense of this part.
instead? I cannot make sense of this part.
12 February, 2017 at 9:06 am
Terence Tao
No, I intend to lie in
to lie in  (thus each of the components
(thus each of the components  ,
,  of this vector are complex numbers). For instance, if
of this vector are complex numbers). For instance, if  and
and  , then
, then  ,
,  , and
, and  .
.
12 February, 2017 at 9:54 am
Anonymous
Ah. When you define ,
, 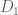 and
and  are used without having a definition… And later, it is said that
are used without having a definition… And later, it is said that
we see that
and
This looks circular. Would you please elaborate what definition do you use for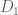 and
and  ?
?
12 February, 2017 at 12:31 pm
nightmartyr
12 February, 2017 at 2:56 pm
Anonymous
Maybe typos in (7). and
and  should be
should be  and
and  I think.
I think.
[Corrected, thanks – T.]
5 June, 2017 at 10:04 am
Five-Value Theorem of Nevanlinna – Elmar Klausmeier's Weblog
[…] 246A, Notes 1: complex differentiation […]
4 September, 2017 at 4:45 am
Anonymous
Do we have the mean value theorem and L’Hopital rule as in real analysis?
4 September, 2017 at 7:12 pm
Terence Tao
L’Hopital’s rule carries over (with basically the same proof), but the mean value theorem is now false. For instance, if is the exponential function, there is no complex number
is the exponential function, there is no complex number  for which
for which 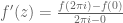 , despite
, despite  being complex differentiable on the entire complex plane. (It is instructive to figure out what property of the real line, that is not shared by the complex numbers, is responsible for the mean value theorem being true for real-valued functions but not complex-valued functions. It is a good exercise to revisit the proof of the real-variable mean value theorem to answer this question.)
being complex differentiable on the entire complex plane. (It is instructive to figure out what property of the real line, that is not shared by the complex numbers, is responsible for the mean value theorem being true for real-valued functions but not complex-valued functions. It is a good exercise to revisit the proof of the real-variable mean value theorem to answer this question.)
5 September, 2017 at 4:07 am
Anonymous
I’m a bit confused with the L’Hopital rule. Rudin gave an example that with
with  and
and 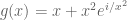 and
and
Is this a contradiction to the L’Hopital rule in complex analysis?
5 September, 2017 at 12:42 pm
Terence Tao
Hmm, you’re right. The argument I had in mind assumed that the denominator was analytic at the limit point, which is not the case in Rudin’s example.
3 November, 2017 at 6:20 am
Cong Ma
I wonder whether the mean value theorem carries over to the Wirtinger derivative. That is for , do we have
, do we have ![f(z_1)-f(z_2) = \int_{0}^{1}\nabla f(z(\tau))d\tau \left[\begin{array}{c} z_{1}-z_{2}\\ \overline{z_{1}-z_{2}} \end{array}\right]](https://s0.wp.com/latex.php?latex=f%28z_1%29-f%28z_2%29+%3D+%5Cint_%7B0%7D%5E%7B1%7D%5Cnabla+f%28z%28%5Ctau%29%29d%5Ctau+%5Cleft%5B%5Cbegin%7Barray%7D%7Bc%7D+z_%7B1%7D-z_%7B2%7D%5C%5C+%5Coverline%7Bz_%7B1%7D-z_%7B2%7D%7D+%5Cend%7Barray%7D%5Cright%5D&bg=ffffff&fg=545454&s=0&c=20201002) , where
, where  ,
,  denotes the conjugate of
denotes the conjugate of  and
and  is the Wirtinger Jacobian.
is the Wirtinger Jacobian.
7 November, 2017 at 4:03 pm
Terence Tao
This identity is true (for continuously differentiable functions ), as can be seen from the fundamental theorem of calculus and the chain rule, but I am not sure if it deserves to be named the mean value theorem.
), as can be seen from the fundamental theorem of calculus and the chain rule, but I am not sure if it deserves to be named the mean value theorem.
7 November, 2017 at 4:47 pm
Cong Ma
Thank you very much!
7 October, 2020 at 8:18 pm
adityaguharoy
Does the mean value theorem fail mainly because we don’t have an ordering of the complex numbers anymore, and so things like the intermediate value property or Rolle’s theorem fail.
In other words, we cannot say that the derivative is zero at a point of extremum because now the extremum doesn’t make sense for a complex valued function anymore.
Is that correct ?
[Yes – T.]
4 September, 2017 at 10:40 pm
Fan
Probably there is a type in Exercise 29 “can real-valued”.
[Corrected, thanks – T.]
11 March, 2018 at 4:01 pm
James Fullwood
In the definition of radius of convergence, should lim inf be replaced with lim sup? (If not, then I am curious as to why most references use lim sup.)
11 March, 2018 at 8:59 pm
Terence Tao
One can write the radius of convergence either as the limit inferior of , or as the reciprocal of the limit superior of
, or as the reciprocal of the limit superior of  ; the two definitions are equivalent.
; the two definitions are equivalent.
27 June, 2018 at 7:42 am
অরিত্র
There’s a typo in exercise 4(iv): the g’s should be replaced by h
[Corrected, thanks – T.]
1 July, 2018 at 6:13 am
Aritra Bhattacharya
What is that in line 3 of proof of proposition 7?
in line 3 of proof of proposition 7?
[HTML formatting error; should be fixed now – T.]
16 November, 2018 at 6:29 am
Aritra Biswas
Respected Sir,
As you mention in the ‘power Series’ section “As it turns out, the region of convergence is always essentially a disk”, I am wandering as to why the region of convergence is essentially a disk and nothing else, i.e I am curious to know if there is any topological subtle reason for such uniform behavior of the region of convergence. Since I am a new-learner, it may happen that my question bears some logical error or pointless per se. I am apologetic beforehand for such occurrences. Pleasr help me go through.
Thank you.
21 November, 2018 at 2:52 pm
Terence Tao
The fact that the region of convergence is a disk (possibly with or without portions of the circular boundary of the disk) is a corollary of the root test. It reflects the fact that if a series converges conditionally, then any other series with exponentially smaller summands will converge absolutely.
5 December, 2018 at 11:07 pm
Aritra Biswas
Thank you Sir. Thanks a lot.
23 December, 2018 at 4:56 pm
keej
Thank you for posting these notes. I have a question (possible typo?)
In Remark 22, regarding the statement “The same preservation of angle is present for real differentiable functions”, do you mean functions from complex numbers to reals, as written, or do you mean functions from reals to reals? If the former, I’m not sure how to interpret what it means for such a map to be conformal.
23 December, 2018 at 10:17 pm
Terence Tao
I meant the latter; I have modified the text to clarify this.
6 April, 2020 at 4:44 am
Maxis Jaisi
I’ve never seen gradient defined for a complex valued function. How do you define the gradient of a map , for example?
, for example?
6 April, 2020 at 9:16 am
Terence Tao
There would be two possible gradients one could use here. In analogy to the gradient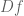 used in these notes, one could define the gradient
used in these notes, one could define the gradient  of a continuously (real) differentiable
of a continuously (real) differentiable 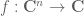 by identifying
by identifying  with
with 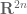 and taking the usual real gradient. If the function
and taking the usual real gradient. If the function  depends holomorphically on its inputs
depends holomorphically on its inputs  (or equivalently if
(or equivalently if  obeys the Cauchy-Riemann equations in each variable separately), one can also define the complex gradient
obeys the Cauchy-Riemann equations in each variable separately), one can also define the complex gradient  as
as 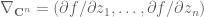 .
.
7 October, 2020 at 2:42 am
Jiayun Meng
At the beginning of section two, shall the denominator of partial derivative in direction of y be ih instead of h?
7 October, 2020 at 3:30 am
Jiayun Meng
Sorry! I understood the material wrongly. It should be h. But I am a bit confused about why it is defined like this. Can I view it as the partial derivative in sense of R^2 plane? Thanks in advance!
12 October, 2020 at 2:36 pm
Ben Johnsrude
Yes, it’s just a partial derivative in the usual sense of a function on R^2 (taking values in the complex plane), the vertical partial derivative. – Ben
7 October, 2020 at 7:58 pm
adityaguharoy
Yesterday during the lectures the following question was asked :
“Does there exist a function which satisfies the Cauchy Riemann equations at a point but is not holomorphic there ?”
The answer is yes (as we all agreed), and here is an example (I will leave the verification for the reader) :
The function satisfies the Cauchy Riemann conditions at
satisfies the Cauchy Riemann conditions at  but is NOT holomorphic there.
but is NOT holomorphic there.
The easiest way to verify is to go via the definition of complex differentiability to verify that is indeed not holomorphic at 0, and the Cauchy Riemann conditions can be verified in a straightforward manner.
is indeed not holomorphic at 0, and the Cauchy Riemann conditions can be verified in a straightforward manner.
7 October, 2020 at 8:05 pm
adityaguharoy
I just forgot to mention that we should have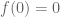 in the above example.
in the above example.
7 October, 2020 at 10:53 pm
Prateek P Kulkarni
Well,it was me who asked the question. My question wasn’t exactly about one point, but your answer has got it all. Thanks for the examples @adityaguharoy
9 October, 2020 at 10:17 am
Anonymous
There are three notions of differentiability at a point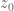 in this set of notes and Stein-Shakarchi’s book.
in this set of notes and Stein-Shakarchi’s book.
(I) The “gradient” (or Fréchet derivative) , defined as the vector
, defined as the vector  with the property that
with the property that
where is the Euclidean norm of
is the Euclidean norm of 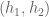 .
.
In this definition, .
.
(II) The complex derivative in Definition 2.
In this definition is a
is a 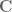 -linear map from
-linear map from 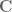 to
to 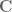 .
.
(III) In Stein-Shakarchi, the complex-valued function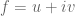 is associated with the mapping
is associated with the mapping 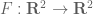 where
where 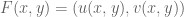 . In this definition,
. In this definition, 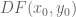 is a
is a 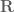 -linear map from
-linear map from 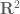 to
to 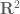 .
.
Are the notions in (I) and (III) equivalent?
9 October, 2020 at 10:51 am
Terence Tao
Yes; the linear map in (III) corresponds in the notation of (I) to the map
in (III) corresponds in the notation of (I) to the map  (identifying
(identifying  with
with 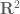 as necessary).
as necessary).
9 October, 2020 at 1:46 pm
Anonymous
Ah. I was confused when trying to identify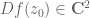 in notion (I) with the
in notion (I) with the  -linear map
-linear map  in notion (III).
in notion (III).
So the map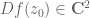 is a
is a 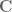 -linear map from
-linear map from 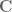 to
to  , not
, not  to
to  . The
. The 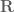 dimensions then match in the two notions.
dimensions then match in the two notions.
9 October, 2020 at 4:22 pm
Anonymous
Maybe it is better to mention that the Fréchet differentiable defined in part two is the real Fréchet differentiable which is a generalization real differentiable so it is weaker than complex differentiable. Nevertheless the complex Fréchet differentiability of a function from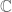 to
to 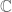 is exactly the complex differentiability in Definition 2 and same for the derivative because complex Fréchet derivative is a generalization of complex derivative.
is exactly the complex differentiability in Definition 2 and same for the derivative because complex Fréchet derivative is a generalization of complex derivative.
12 October, 2020 at 9:59 am
Anonymous
Can one adapt the proof of Theorem 25 to show the strong version of the maximum principle?
12 October, 2020 at 10:16 am
Terence Tao
Hmm, with a fair amount of additional effort, yes, but I don’t know of a proof of comparable length to this one. (At a bare minimum, one now has to use the fact that the domain is connected.) If one has an additional tool such as the mean value theorem or Harnack’s inequality then it is straightforward, but the “first principles” proofs I am aware of are somewhat lengthy.
14 October, 2020 at 7:29 am
Anonymous
I am confused by the statement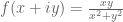 has partial derivatives
has partial derivatives 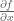 and
and  exist at f(0). Aren’t they both 0/0?
exist at f(0). Aren’t they both 0/0?
14 October, 2020 at 10:47 am
Terence Tao
No; try computing the partial derivatives from first principles.
14 October, 2020 at 11:22 am
Anonymous
Thank you! Now that makes sense. Why do the two processes give different results?
14 October, 2020 at 12:24 pm
Anonymous
Because partial derivatives need not be the same.
14 October, 2020 at 6:24 pm
max_principle
In the proof of maximum principle, we have , clearly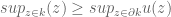 .why?
.why?
15 October, 2020 at 8:45 am
Anonymous
K is compact, so attains its sup (either in interior of K or on boundary of K). Think of it as a generalization of Bolzano–Weierstrass theorem.
15 October, 2020 at 10:40 am
Anonymous
Simply because is a subset of
is a subset of  .
.
16 October, 2020 at 5:06 pm
Anonymous
In the proof of Theorem 15, as , you said each summand converges to
, you said each summand converges to  . Where does the
. Where does the  come from? I thought it is just
come from? I thought it is just  .
.
[Here the summand refers to the summand of the series . (The summand is itself a sum of
. (The summand is itself a sum of  sub-summands, each of which converge individually to
sub-summands, each of which converge individually to  .) -T]
.) -T]
25 October, 2020 at 6:16 am
Anonymous
In the proof Proposition 28,
… The fact that
I think here “ ” should be “
” should be “ ” since one is not defining the partial derivative on the left but concluding it from (18).
” since one is not defining the partial derivative on the left but concluding it from (18).
[Corrected – T.]
13 December, 2020 at 5:50 pm
Anonymous
The Newton quotient is also used in the proof of Theorem 27 and 30 (the two fundamental theorems of calculus) in Notes 2. Instead of proving from the first principle as in this set of notes, can one somehow use the FTCs to show Theorem 15 in a non-circular way? (It seems that Theorem 15 has been used in various places in later notes.)
[Yes, this is possible, and I encourage you to work out this as an exercise -T.]
13 December, 2020 at 6:00 pm
Anonymous
As
should be
… converges to
This almost proves the desired limiting formula
but we need to justify the interchange of a sum and limit.
The right-hand side should be ?
?
[Corrected, thanks – T.]
23 January, 2021 at 12:56 pm
246B, Notes 2: Some connections with the Fourier transform | What's new
[…] maximum modulus principle (Exercise 26 from 246A Notes 1) for holomorphic functions asserts that if a function continuous on a compact subset of the plane […]
27 September, 2021 at 8:59 am
246A, Notes 0: the complex numbers | What's new
[…] Next set of notes: Notes 1. […]
27 September, 2021 at 9:02 am
246A, Notes 2: complex integration | What's new
[…] set of notes: Notes 1. Next set of notes: Notes […]
10 January, 2022 at 6:48 am
kirtanvora
There’s a typo in a paragraph after exercise 17, 2^{n-1} should be 2^{n+1}
[Corrected, thanks – T.]
27 December, 2022 at 5:42 am
Anonymous
By Exercise 17, given a sequence , if
, if  is a power series with a positive radius of convergence, then
is a power series with a positive radius of convergence, then  for all
for all  . If the mentioned power series fails to have a positive radius of convergence, can one still construct a smooth function
. If the mentioned power series fails to have a positive radius of convergence, can one still construct a smooth function  with
with  for all
for all  ?
?
31 December, 2022 at 7:03 pm
Terence Tao
For real-variable functions, this is the zero-dimensional case of Borel’s lemma. For complex-variable functions, it hinges on what you mean by “smooth”. Functions that are complex differentiable in a neighbourhood of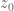 are analytic and so the Taylor series has to have a positive radius of convergence.
are analytic and so the Taylor series has to have a positive radius of convergence.
29 December, 2022 at 7:12 am
Anonymous
Some part of the formula is missing in (7)



[Changed to
to 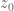 -T.]
-T.]