Let be a field, and let
be a finite extension of that field; in this post we will denote such a relationship by
. We say that
is a Galois extension of
if the cardinality of the automorphism group
of
fixing
is as large as it can be, namely the degree
of the extension. In that case, we call
the Galois group of
over
and denote it also by
. The fundamental theorem of Galois theory then gives a one-to-one correspondence (also known as the Galois correspondence) between the intermediate extensions between
and
and the subgroups of
:
Theorem 1 (Fundamental theorem of Galois theory) Let
be a Galois extension of
.
- (i) If
is an intermediate field betwen
and
, then
is a Galois extension of
, and
is a subgroup of
.
- (ii) Conversely, if
is a subgroup of
, then there is a unique intermediate field
such that
; namely
is the set of elements of
that are fixed by
.
- (iii) If
and
, then
if and only if
is a subgroup of
.
- (iv) If
is an intermediate field between
and
, then
is a Galois extension of
if and only if
is a normal subgroup of
. In that case,
is isomorphic to the quotient group
.
Example 2 Let
, and let
be the degree
Galois extension formed by adjoining a primitive
root of unity (that is to say,
is the cyclotomic field of order
). Then
is isomorphic to the multiplicative cyclic group
(the invertible elements of the ring
). Amongst the intermediate fields, one has the cyclotomic fields of the form
where
divides
; they are also Galois extensions, with
isomorphic to
and
isomorphic to the elements
of
such that
modulo
. (There can also be other intermediate fields, corresponding to other subgroups of
.)
Example 3 Let
be the field of rational functions of one indeterminate
with complex coefficients, and let
be the field formed by adjoining an
root
to
, thus
. Then
is a degree
Galois extension of
with Galois group isomorphic to
(with an element
corresponding to the field automorphism of
that sends
to
). The intermediate fields are of the form
where
divides
; they are also Galois extensions, with
isomorphic to
and
isomorphic to the multiples of
in
.
There is an analogous Galois correspondence in the covering theory of manifolds. For simplicity we restrict attention to finite covers. If is a connected manifold and
is a finite covering map of
by another connected manifold
, we denote this relationship by
. (Later on we will change our function notations slightly and write
in place of the more traditional
, and similarly for the deck transformations
below; more on this below the fold.) If
, we can define
to be the group of deck transformations: continuous maps
which preserve the fibres of
. We say that this covering map is a Galois cover if the cardinality of the group
is as large as it can be. In that case we call
the Galois group of
over
and denote it by
.
Suppose is a finite cover of
. An intermediate cover
between
and
is a cover of
by
, such that
, in such a way that the covering maps are compatible, in the sense that
is the composition of
and
. This sort of compatibilty condition will be implicitly assumed whenever we chain together multiple instances of the
notation. Two intermediate covers
are equivalent if they cover each other, in a fashion compatible with all the other covering maps, thus
and
. We then have the analogous Galois correspondence:
Theorem 4 (Fundamental theorem of covering spaces) Let
be a Galois covering.
- (i) If
is an intermediate cover betwen
and
, then
is a Galois extension of
, and
is a subgroup of
.
- (ii) Conversely, if
is a subgroup of
, then there is a intermediate cover
, unique up to equivalence, such that
.
- (iii) If
and
, then
if and only if
is a subgroup of
.
- (iv) If
, then
is a Galois cover of
if and only if
is a normal subgroup of
. In that case,
is isomorphic to the quotient group
.
Example 5 Let
, and let
be the
-fold cover of
with covering map
. Then
is a Galois cover of
, and
is isomorphic to the cyclic group
. The intermediate covers are (up to equivalence) of the form
with covering map
where
divides
; they are also Galois covers, with
isomorphic to
and
isomorphic to the multiples of
in
.
Given the strong similarity between the two theorems, it is natural to ask if there is some more concrete connection between Galois theory and the theory of finite covers.
In one direction, if the manifolds have an algebraic structure (or a complex structure), then one can relate covering spaces to field extensions by considering the field of rational functions (or meromorphic functions) on the space. For instance, if
and
is the coordinate on
, one can consider the field
of rational functions on
; the
-fold cover
with coordinate
from Example 5 similarly has a field
of rational functions. The covering
relates the two coordinates
by the relation
, at which point one sees that the rational functions
on
are a degree
extension of that of
(formed by adjoining the
root of unity
to
). In this way we see that Example 5 is in fact closely related to Example 3.
Exercise 6 What happens if one uses meromorphic functions in place of rational functions in the above example? (To answer this question, I found it convenient to use a discrete Fourier transform associated to the multiplicative action of the
roots of unity on
to decompose the meromorphic functions on
as a linear combination of functions invariant under this action, times a power
of the coordinate
for
.)
I was curious however about the reverse direction. Starting with some field extensions , is it is possible to create manifold like spaces
associated to these fields in such a fashion that (say)
behaves like a “covering space” to
with a group
of deck transformations isomorphic to
, so that the Galois correspondences agree? Also, given how the notion of a path (and associated concepts such as loops, monodromy and the fundamental group) play a prominent role in the theory of covering spaces, can spaces such as
or
also come with a notion of a path that is somehow compatible with the Galois correspondence?
The standard answer from modern algebraic geometry (as articulated for instance in this nice MathOverflow answer by Minhyong Kim) is to set equal to the spectrum
of the field
. As a set, the spectrum
of a commutative ring
is defined as the set of prime ideals of
. Generally speaking, the map
that maps a commutative ring to its spectrum tends to act like an inverse of the operation that maps a space
to a ring of functions on that space. For instance, if one considers the commutative ring
of regular functions on
, then each point
in
gives rise to the prime ideal
, and one can check that these are the only such prime ideals (other than the zero ideal
), giving an almost one-to-one correspondence between
and
. (The zero ideal corresponds instead to the generic point of
.)
Of course, the spectrum of a field such as is just a point, as the zero ideal
is the only prime ideal. Naively, it would then seem that there is not enough space inside such a point to support a rich enough structure of paths to recover the Galois theory of this field. In modern algebraic geometry, one addresses this issue by considering not just the set-theoretic elements of
, but more general “base points”
that map from some other (affine) scheme
to
(one could also consider non-affine base points of course). One has to rework many of the fundamentals of the subject to accommodate this “relative point of view“, for instance replacing the usual notion of topology with an étale topology, but once one does so one obtains a very satisfactory theory.
As an exercise, I set myself the task of trying to interpret Galois theory as an analogue of covering space theory in a more classical fashion, without explicit reference to more modern concepts such as schemes, spectra, or étale topology. After some experimentation, I found a reasonably satisfactory way to do so as follows. The space that one associates with
in this classical perspective is not the single point
, but instead the much larger space consisting of ring homomorphisms
from
to arbitrary integral domains
; informally,
consists of all the “models” or “representations” of
(in the spirit of this previous blog post). (There is a technical set-theoretic issue here because the class of integral domains
is a proper class, so that
will also be a proper class; I will completely ignore such technicalities in this post.) We view each such homomorphism
as a single point in
. The analogous notion of a path from one point
to another
is then a homomorphism
of integral domains, such that
is the composition of
with
. Note that every prime ideal
in the spectrum
of a commutative ring
gives rise to a point
in the space
defined here, namely the quotient map
to the ring
, which is an integral domain because
is prime. So one can think of
as being a distinguished subset of
; alternatively, one can think of
as a sort of “penumbra” surrounding
. In particular, when
is a field,
defines a special point
in
, namely the identity homomorphism
.
Below the fold I would like to record this interpretation of Galois theory, by first revisiting the theory of covering spaces using paths as the basic building block, and then adapting that theory to the theory of field extensions using the spaces indicated above. This is not too far from the usual scheme-theoretic way of phrasing the connection between the two topics (basically I have replaced étale-type points with more classical points
), but I had not seen it explicitly articulated before, so I am recording it here for my own benefit and for any other readers who may be interested.
— 1. Some notation on functions —
It will be convenient to adopt notation in which many of the basic hypotheses we use take the form of an associativity-type law. To this end, we will use two non-standard notations for functions (which is implicit in the usual notation for left and right group actions), sometimes referred to as reverse Polish and Polish notation (for left and right actions respectively).
Definition 7 (Polish and reverse Polish notation) Let
be sets. A function
acting on the right is a function
in which the notation for evaluating
at an element
is denoted
rather than the more standard
. If
are two functions acting on the right, we write
for the composition that is more commonly denoted
; this way we have the associativity-type property
Similarly, a function
acting on the left is a function
in which the notation for evaluating
at an element
is denoted
rather than the more standard
. If
are two functions acting on the left, we write
for the composition that is more commonly denoted
; this way we have the associativity type property
for
. We do not define a composition between a function acting on the right and a function acting on the left.
Remark 8 Functions acting on the left largely correspond to the traditional notion of a function, despite the reversed arrow in the notation
; functions acting on the right can be thought of as “antifunctions”, in which the composition law is reversed.
As a general rule, in this post covering maps and deck transformations will be functions acting on the left, while paths will be functions acting on the right.
When viewing the (left or right) automorphisms of a set as a group, we use juxtaposition
rather than composition
as the group law; thus, in the case of automorphisms acting on the right, the group structure we will use is the opposite of the usual composition group structure, whereas for automorphisms acting on the left the group structure agrees with the standard composition group structure. In particular, the group of right-automorphisms of a space
is canonically identified with the opposite group of the group of left-automorphisms of a space
. (Of course, the opposite of a group
is in turn canonically identified with the group itself through the inversion operation
, but we will refrain from using this further identification in this text as it can cause some additional confusion.)
As is customary, we will adopt the notational convention of omitting parentheses whenever there is an associativity-type law to prevent any ambiguity. For instance, if and
,
are functions acting on the right, we may write
without any ambiguity thanks to (1).
— 2. Covers of manifolds —
We begin by revisiting the theory of covering spaces of manifolds. To align with the way we will be thinking about Galois theory, it will be convenient to assume the existence of a (connected) base manifold , such that all the other manifolds
we will be considering are finite extensions of that base
. Again, for simplicity (and to make the theory more closely resemble Galois theory) we will restrict attention to finite covers, though one could extend most of this discussion to infinite covers without much difficulty.
One can think of the base manifold as a category, in which the objects are the points
of the manifold, and the morphisms are the paths
in
connecting one point
to another
, with the composition
of two paths
(connecting
to
) with
(connecting
to
) being a path connecting
with
formed by concatenating the two paths together. We leave the composition
undefined if the terminal point of
does not agree with the starting point of
. We will not distinguish a path from a reparameterisation of that path (in fact we will not mention parameterisations at all); in particular, we have the associativity law
We denote the space of all paths (up to reparameterisations) by . One should think of
as being somewhat like a group, except that the multiplication law is not always defined. (More precisely,
is not just a category, but is in fact a groupoid, although we will not explicitly use this fact here.)
To signify the fact that a path has starting point
and terminal point
, we write
If is not the starting point of
, we leave
undefined. Note this way that we obtain the associativity-type law
whenever one of the two sides is well-defined (which forces the other side to be well-defined also).
Now let be a finite cover with covering map
; here all covering maps are understood to act on the left. Given a point
lying above a base point
(thus
), and a path
with starting point
, we may lift
up to a path in
that starts at
and ends at some point which we will denote by
. This point will lie above
in
, thus we have the associativity-type law
whenever one of the two sides (and hence the other) is well-defined. It is easy to see that this defines an (right) action of in the sense that one has the associativity type law
whenever and
are such that one of the two sides (and hence the other) is well-defined.
Note that if is connected and
, then any other point
can be connected to
by a path in
, which is the lift of some path in
. Thus the action of
is transitive in the sense that for every
there exists
such that
.
If we have finite covers then the actions of
on
and
are compatible in the sense that one has the associativity-type law
whenever one of the two sides (and hence the other) is well-defined. A deck transformation of (viewed as a cover of
) is a continuous map
(acting on the left) such that
The space of deck transformations is clearly a group that acts on the left on
. By working locally we see that deck transformations map lifts to lifts, thus one has the associativity-type law
whenever ,
,
are such that one of the two sides (and hence the other) is well-defined. Conversely, one can check that any map
that obeys the two properties (2), (3) is a deck transformation (even without assuming continuity of
!). Hence one can in fact take (2), (3) to be the definition of a deck transformation; all the topological structure is now concealed within the path groupoid
and its actions on
and
.
One consequence of (3) is that the action of this group is free: if
is such that
for some point
, then we also have
whenever
makes sense, and hence by transitivity
for all
, so
is the identity.
In particular, if is a degree
cover of
(so that all fibres
for
have cardinality
), then the order of the group
cannot exceed
, since the orbit
of any given point under this free action lies in a fibre of
above
and has the same cardinality as
. If the order equals
, we say that the cover is a Galois cover, use
to denote the group
, and conclude that the action of
is transitive on fibres. Thus, if
are such that
, then there exists a unique
such that
.
We can now prove Theorem 4. Let be a degree
cover. Let
be an intermediate cover between
and
, and suppose that
has degree
over
. A fibre
of
over
has degree
, and splits into
fibres
of
over
, each of which has cardinality
(so in particular
divides
). Pick one of these fibres, and pick a point
in it. By the above discussion, there are precisely
elements
of
such that
lies in the same fibre over
as
:
Applying paths in on the right and using transitivity (and associativity), we conclude that
, thus
. As we have located
elements of this group, this is in fact the entire group of automorphisms, so we conclude that
is a Galois cover of
and
is a subgroup of
. This proves part (i) of the theorem.
A similar argument shows that if then
is a subgroup of
. In particular, if
and
are equivalent then
. Conversely, suppose that
and
are such that
is a subgroup of
. If
are such that
, then by the Galois nature of
over
we can find
such that
. But then
, hence
. Thus we can factor
for some uniquely defined function
. It is not hard to verify that
is a finite covering map that is compatible with the existing covering maps, and hence
. This proves (iii). Reversing the roles of
and
, we conclude in particular that if
then
and
are equivalent. This gives the “unique up to equivalence” portion of (ii).
To finish the proof of (ii), let be a subgroup of
, then we can define an equivalence relation
on
by declaring
for every
and
. If we set
to be the quotient space
with the obvious quotient map
, then one has
whenever
(which is equivalent to
). Thus we may factor
for some unique map . One may easily verify that
are both covering maps, so that we have
. To finish the proof of (Ii) we need to show that
. Unpacking the definitions, our goal is to show that
is the set of all
such that
for all
. Clearly if
then
for all
. Conversely, suppose that
is such that
for all
. In particular, if one fixed a point
, then
for some
. This implies that
for all
; but the action of
on
is transitive, and hence
, giving the claim.
Finally, we prove (iv). By parts (i), (ii), we may assume without loss of generality that , where
if
for some
.
First suppose that is a normal subgroup of
. Then
implies
whenever
and
. Thus the action of
on
descends to that of
; since the former is transitive on fibres above
, so is the latter. Hence
is a Galois extension of
. Conversely, suppose that
is Galois. Then for any
and
, there must exist
such that
. Since the right action of
on
is transitive,
does not actually depend on
, and is uniquely specified by
. Replacing
by
for any
, we have
but , hence
or equivalently . This implies that
, thus
is preserved by conjugation by arbitrary elements
of
. In other words,
is a normal subgroup. The map
described here can easily be verified to be a homomorphism from
to
with kernel
, so the claim (iv) follows from the first isomorphism theorem.
Remark 9 Let
be a Galois cover, let
be a point in the base
, and let
be a point in the fibre
. For any loop
starting and ending at
(so that
, the point
lies in the same fibre
of
as
, hence by the Galois nature of the cover there is a unique
such that
It is easy to see that homotopic deformations of
(preserving the initial and final point
) do not affect the value of
. Thus, we have constructed a map
from the fundamental group
of
at
to the Galois group
, such that
As
is connected, we see that this map is surjective. From (4) and the fact that that
acts freely on
) we also see that the map is a homomorphism. (In many texts, the notation is set up so that this correspondence is an antihomomorphism rather than a homomorphism; we have avoided this by making the paths act on the right and the deck transformations act on the left, thus implicitly introducing an order reversal when identifying the two.) Thus we see that the Galois group
is isomorphic to a quotient of the fundamental group
. However, this isomorphism is not canonical, even if one fixes the base point
, because it depends on
! If one replaces
by another point
in the same fibre for some
, then the associated map
, defined by
has to be conjugate to
in order to remain compatible with (4):
Thus, if one does not specify the reference point
in the covering space
, the identification of
with a quotient of
is only unique up to conjugation. Thus the relationship between fundamental groups and Galois groups are a little subtle, requiring one to be aware of what base points have been selected, unless one is willing to just work up to conjugacy. (See also the above-mentioned post of Kim for some further discussion of this point.)
— 3. Extensions of fields —
We can now give an analogous treatment of the Galois correspondence for finite extensions of fields.
In this setting, we will take the base space to be the category of integral domains (with morphisms now interpreted as “paths”). Thus, points
in this space are integral domains, and the paths in this space are ring homomorphisms
from one integral domain to another, which we will think of as functions acting on the right, in particular the composition of
and
will be denoted
(rather than the more traditional
). As before, we use the notation
to denote the assertion that
is a ring homomorphism from
to
, so in particular we have the associativity type law
whenever either side is well-defined. As previously mentioned, we will ignore all set-theoretic issues caused by the fact that is a proper class rather than a set, and similarly for the covers of
introduced below. We let
denote the collection of all ring homomorphisms
connecting points in
. This is analogous to the space of collections of paths in the base manifold
in the covering space context. Oen caveat however is that while paths in manifolds always have inverses, the same is not true in
, because not every ring homomorphism between integral domains is invertible. This complicates the situation somewhat compared to the covering space case, but it turns out that the additional level of complication is manageable.
Given a field , we define an associated space
, whose points
are ring homomorphisms
to some ring
, where we view these homomorphism as acting on the right. There is an obvious map
(viewed as a function acting on the left) that maps a ring homomorphism
to its codomain
. If
,
are such that
and
, then the composition
is a ring homomorphism from
to
and is thus also an element of
. Thus
acts on the right on
in the sense that
whenever either side is well-defined, and the action is compatible with the base in the sense that
whenever either side is well-defined.
Remark 10 One can define
for any commutative ring
in the same fashion. If one takes
to be the integers
, then
is in one-to-one correspondence with
, since for every integral domain
there is a unique ring homomorphism from
to
. Thus we are really thinking of all our spaces
as being covers of
. In the usual scheme-theoretic language, one views the schemes
as lying above the base scheme
.
Remark 11 The characteristic of the field
naturally restricts the base points
that
actually lies above. For instance, if
has characteristic zero, then points
of
only lie above those base points
for which the unit
of
has infinite order; similarly, if
has a positive characteristic
, then points of
only lie above base points
for which the unit of
has order
. This helps explain why fields of different characteristic seem to inhabit “different worlds” – they lie above disjoint (and disconnected) portions of the base space
! However, we will not exploit the field characteristic in this post.
As mentioned in the introduction, each space has a distinguished point
, which is the identity map on
and is the representative in this formalism of
. This point makes
is “directionally connected” in the following sense: every other point
in
is connected to
by a path
in the sense that
. Indeed, one just takes
to be precisely the same homomorphism as
. (More generally, in every commutative ring
, every point
of
will be connected via a path from a point in
, namely the kernel of
which is necessarily a prime ideal since
is an integral domain. I like to think of
as a sort of “penumbra” lurking around the much smaller set
.) However, the connectedness does not flow the other way: not every point
in
is connected back to
by a path, because paths need not be invertible. (For instance, if
is an embedding of
into a larger field
, there is no way to map
back into
by a ring homomorphism while preserving
, as homomorphisms of fields have to be injective.)
Suppose we have a finite extension of fields, then the inclusion map
, viewed as a function acting on the right, is a ring homomorphism. As such, it also can be viewed as a map from
to
: any point
of
, when composed with
, gives rise to a point
of
. We relabel this composition map as
(now viewed as a function acting on the left), thus
for all . By construction we see that
and similarly for any nested sequence of fields one has
Now let us look at the fibres of above
. We need the following basic result, which relates the degree of the field extension
to the degree of the cover
:
Proposition 12 Let
be a degree
extension of a field
. Then every fibre
in
of a point
in
has cardinality at most
.
Proof: Unpacking all the definitions, we are asking to show that every ring homomorphism into an integral domain
has at most
extensions to a ring homomorphism
.
We induct on . If
the claim is trivial, so suppose
and the claim has already been proven for smaller values of
. Then
is larger than
, so we may find an element
that lies in
but not
. Let
be the degree of
, thus
,
is a degree
extension of
and
is a degree
extension of
(in particular,
divides
). By induction hypothesis, every ring homomorphism on
has at most
extensions to
, so it suffices to show that
has at most
extensions to
.
Let be the minimal polynomial of
with coefficients in
, thus
is monic with degree
, and
. Any extension
of
to
must obey the law
, where
is the monic polynomial of degree
with coefficients in
formed by applying
to each coefficient of
. As
is an integral domain,
has at most
roots. Thus there are at most
possible values of
; since
is completely determined by
and
, we obtain the claim.
Example 13 Let
and
be the fields from Example 3. The inclusion map
is a point in
. The fibre
consists of
points
, with
being the field automorphism of
that sends
to
(in particular,
is the distinguished point
of
). In contrast, the distinguished point
of
has empty fibre
, since there is no ring homomorphism from
to
that fixes
.
Remark 14 If two points
in
are connected by an invertible path
, thus
and
, then it is easy to see that
induces a one-to-one correspondence between the fibre
and the fibre
; in particular, the two have the same cardinality. However, in contrast to the situation with covering spaces, not all paths are invertible, and so the cardinality of a fibre
can vary with the base
, as can already be seen in the preceding example. However the situation is better for Galois extensions, as we shall shortly see, in which all non-empty fibres are isomorphic.
We continue analysing a field extension , viewing
as analogous to a covering space for
. By analogy with covering spaces, we could define a “deck transformation” of
over
to be a map
(acting on the left) such that
whenever ,
are such that one side (and hence the other) of the above equation is well-defined. Let us see what a deck transformation actually is. If we apply
to the distinguished point
of
, we obtain a ring homomorphism
. From (5) we have
which on chasing definitions means that is the identity on
. Thus
is a
-linear map; it also preserves
, so it has trivial kernel and is thus injective. As
is finite dimensional over
, it is also surjective; hence
is in fact a field automorphism of
that fixes
. The action of
on any other point
of
can then be computed by writing
where
is the path connecting
to
and using (6) to conclude that
. Conversely, given any field automorphism
that fixes
, one can generate a deck transformation
by setting
for all ring homomorphisms
; by chasing definitions one verifies that this is a deck transformation. Thus we have a one-to-one correspondence between deck transformations and field automorphisms of
fixing
. (This correspondence feels reminiscent of the Yoneda lemma, though I was not able to find a direct link between the two.)
Exercise 15 Show that the correspondence between deck transformations and field automorphisms given above is a group isomorphism. (When functions are expressed in more traditional language, this correspondence is an antiisomorphism rather than an isomorphism. We are able to avoid this reversal of order by making deck transformations act on the left and field automorphisms act on the right.)
One consequence of the above correspondence is that the space of deck transformations of
over
is in one-to-one correspondence with the group
of field automorphisms of
fixing
. If
is an intermediate field, then certainly any deck transformation of
over
is also a deck transformation of
over
, so
is a subgroup of
.
From the above discussion, we see that a deck transformation of over
is completely determined by its action on the distinguished point
. In particular, the action of
is free on the distinguished point
of
in the sense that the points
for
are all distinct. As they also lie in the same fibre of
above
, we conclude from Proposition 12 that the order of
cannot exceed the degree of the extension:
As stated in the introduction, we call a Galois extension of
if we in fact have equality
and then we rename as
. This is canonically equivalent to the usual Galois group
over fields. Thus, if
is a degree
Galois extension of
, then implies that the fibre containing
above
must have cardinality exactly
, with
acting freely and transitively on this fibre. In fact the same is true for every non-empty fibre:
Lemma 16 Let
be a degree
Galois extension of
, and let
be a point in
. Then the fibre
containing
above
has cardinality exactly
, and
acts freely and transitively on this fibre. In other words, whenever
are such that
, then there is a unique
such that
.
Proof: As is a field and
is an integral domain, the ring homomorphism
must be injective (it maps invertible elements to invertible elements, and hence maps non-zero elements to non-zero elements). Each Galois group element
corresponds to a different field automorphism of
, hence the
homomorphisms
,
are all distinct. This produces
distinct elements of the fibre of
; by Proposition 12 this is the entire fibre. The claim follows.
Thanks to this lemma, we see that behaves like a degree
covering map on some subset of
(the space of ring homomorphisms
for which
is “large enough” that there is at least one extension of
to
).
We can now prove part (i) of Theorem 1, in analogy with the covering space theory argument:
Proposition 17 If
is a Galois extension of
, and
is an intermediate field, then
is a Galois extension of
.
Note that we have already demonstrated that is a subgroup of
, so this proposition completes the proof of Theorem 1(i).
Proof: Let denote the degree of
over
, and
the degree of
over
, thus
is a degree
extension of
. Consider a non-empty fibre of
above
. By Lemma 16, this fibre consists of
points. It also can be decomposed into fibres of
above
, indexed by a fibre of
above
. By Lemma 16, the latter fibre consists of
points, while by Proposition 12, the former fibres all have cardinality at most
. Hence all the former fibres must have cardinality exactly
. In particular, the fibre of
above
has cardinality
. This fibre consists of those ring homomorphisms
that fix
. As discussed previously, these ring homomorphisms must be field automorphisms, and thus generate elements of
(or
. Thus
has cardinality at least
, and hence by (7) it has cardinality exactly
. Thus
is a Galois extension of
as required.
Proof: By definition, every element of is fixed by
, thus
and hence
On the other hand, by Proposition 17 we have . Finally, from (7) we have
Therefore all inequalities must be equalities, and as claimed.
Now we prove Theorem 1(ii). Let be a subgroup of
, which we can also identify with a subgroup of
. Let
denote the set of elements of
that are fixed by
; this is clearly an intermediate field between
and
:
On the one hand, every element of can be identified with an element of
. By Proposition 17,
has order exactly equal to
. Thus
To prove the reverse inequality, we use an argument of Artin. We first need a simple lemma:
Lemma 19 (Producing an invariant vector) Let the notation be as above. Let
be the
-fold Cartesian product of
(viewed as a vector space over
), and let
act componentwise on
:
Let
be an
-invariant subspace of
(i.e.,
is a vector space over
such that
whenever
and
). If
contains a non-zero element of
, then it also contains a non-zero element of
.
Proof: Let be a non-zero element of
with a minimal number of non-zero entries. By relabeling, we may assume that
is non-zero; by dividing by
, we may normalise
. If all the other coefficients lie in
then we are done; by relabeling we may thus assume without loss of generality that
. By definition of
, we may thus find
such that
. The vector
is then a non-zero element of
with fewer non-zero entries than
, contradicting the minimality of
, and the claim follows.
Remark 20 This argument is reminiscent of the abstract ergodic theorem from this previous blog post, except that now we minimise the
norm rather than the
norm, since the latter is unavailable over arbitrary fields
. While this lemma is simple, it seems to be the one aspect of the Galois correspondence for field extensions that does not seem to have an obvious analogue in the covering space setting; on the other hand, I do not know how to prove the fundamental theorem of Galois theory without this lemma or something like it (though presumably the original arguments of Galois proceed differently).
Corollary 21 We have
.
Proof: Suppose for contradiction that , thus we may find elements
of
that are linearly independent over
. We form a vector
out of these elements, and consider the orbit
of this vector. Let
be the space of vectors orthogonal to this orbit, where we use the usual dot product
in . This space has codimension at most
in
and thus has a non-zero vector since
. Clearly
is
-invariant. By Lemma 19,
contains a non-zero vector
whose entries lie in
. By construction,
is orthogonal to
, thus there is a non-trivial linear relation amongst the
with coefficients in
, contradicting linear independence.
We thus have , giving the existence part of Theorem 1(ii); the uniqueness part is immediate from Corollary 18.
Theorem 1(iii) is also immediate from Corollary 18, so we turn to Theorem 1(iv). Let . First suppose that
is a normal subgroup of
. If
and
, then
fixes
, thus
fixes
. Thus
, hence by Corollary 17 we have
. Thus the action of
descends to that of
; equivalently, every deck transformation of
above
descends to a deck transformation of
above
. Since the fibre of
above
has cardinality
, and splits into fibres of cardinality
above
indexed by a fibre of
above
that has cardinality at most
by Proposition 12, and
, we conclude that the latter fibre must have cardinality exactly
. As
acts transitively on the fibre of
, it must also act transitively on this fibre of
. Thus there at least
distinct deck transformations of
above
, and so
is a Galois extension of
thanks to (7), and every deck transformation of
above
arises from a deck transformation of
above
. Thus we have constructed a surjective map from
to
which can easily be verified to be a homomorphism. The kernel of this homomorphism consists of all deck transformations of
above
that preserve the fibres of
above
; applying the deck transformation to the distinguished point
, one sees in particular that the field automorphism of
associated to this transformation preserves
, and hence this transformation lies in
. Conversely every deck transformation in
descends to the identity transformation on
. Thus the kernel of the homomorphism is precisely
, and the isomorphism of
with
then follows from the first isomorphism theorem.
Conversely, suppose that is a Galois extension of
. Let
and
. The points
,
of
lie above the same point of
; from Lemma 16 there thus exists
such that
On the other hand, as is the distinguished point of
, there exists
such that
. Applying
on the right to the above equation, we thus have
But lie above the same point of
, thus
, and hence
By Lemma 16 again, this implies that for some
. As
connects to every other point in
by a path in
, we conclude that
, thus
. In other words,
is a normal subgroup of
.

18 comments
Comments feed for this article
28 August, 2018 at 2:38 pm
Fausto di Biase
This seems reminiscent of some recent work of Peter Scholze.
28 August, 2018 at 6:28 pm
test
No it doesn’t.
29 August, 2018 at 6:46 am
Ben Spitz
I think part (iv) of the fundamental theorem of galois theory should say that Gal(F/k) is isomorphic to Gal(E/k)/Gal(E/F)
[Corrected, thanks – T.]
4 September, 2018 at 12:16 pm
Anonymous
I still see the wrong version.
[Hopefully fixed for good now – T.]
29 August, 2018 at 1:09 pm
Trying to understand the Galois correspondence | What's new - Nevin Manimala's Blog
[…] by /u/tick_tock_clock [link] […]
29 August, 2018 at 1:40 pm
Frank Murphy
Reblogged this on fmurphyrng.
29 August, 2018 at 2:08 pm
hmmm
Are there nice geometric reformulations of the classical applications of Galois theory (solvability in radicals of the quintic, ruler-and-compass constructions, and the like), in terms of deck coverings?
29 August, 2018 at 4:18 pm
Terence Tao
For trisection, I did something like this in this previous blog post. For unsolvability of the quintic by radicals, there is a Riemann surface argument of Arnold which one can think of as a covering space argument.
29 August, 2018 at 4:33 pm
francisrlb
In the last paragraph, is there an issue in saying that M_{F} is a quotient of M_{E}, since the point 1 : F -> F, would need to come from a map E -> F?
29 August, 2018 at 8:59 pm
Terence Tao
Oops, you’re right, the argument here is a little trickier than in the covering space case (and also I forgot to write up the converse implication for this step). I’ve rewritten the argument to fix this.
30 August, 2018 at 5:03 am
Akshaya
Dear Terry,
Could you please try to similarly explain Etale topology, cohomology, point-counting trace formula?
31 August, 2018 at 4:30 pm
Quick Links | Not Even Wrong
[…] Terry Tao has come up with his own take on arithmetic geometry, available here. […]
3 September, 2018 at 8:35 am
Anonymous
Dear Terry,
I would like to confide with you some words:Last night, I had a strange dream.I found that you solved 6 clay millenium problems that I could arrange the order of them below:
*1)Yang-Mills existence and mass gaps
*2)Navier-Stokes existence and smoothness
*3)Riemann hypothesis
*4)Birch-Swinerton Dyer conjecture
*5)Hodge conjecture
*6)P vs NP
In all of them, I found that Yang Mills you solved very quickly.You had too many proofs for Navier Stokes.Riemann is the best difficult problem in all of 7 ,because I found that you spend a lot of time doing it.
Aha,there are many things that science never can prove.Many great inventions which comes from a dream.I do not need anyone believe this.Pro.Tao will see my dream is right
4 September, 2018 at 9:33 am
Nick
Terry: Great exposition. However, in Example 2 (under Theorem 1), I don’t think any intermediate field of a cyclotomic extension is another cyclotomic extension. For example, if you take the fixed field of a cyclotomic extension under complex conjugation, it will consist of real numbers and so generally is not a cyclotomic extension.
You probably meant to say “some intermediate fields are of the form”.
[Oops, had overlooked that point. Corrected now, thanks – T.]
7 September, 2018 at 2:30 am
mathcination
I assume this is strongly related to the following book:
Khovanskii: Galois Theory, Coverings, and Riemann Surfaces
https://www.springer.com/de/book/9783642388408
7 September, 2018 at 7:45 am
Terence Tao
Yes, I should have mentioned some references on this (I am partial to Szamuely’s “Galois groups and fundamental groups“, for instance). For fields of meromorphic functions on Riemann surfaces and their finite covers there is a very close correspondence between the Galois groups of the fields and the (profinite completion of the) fundamental groups of the Riemann surfaces, as is discussed in Szamuely’s book (and presumably also in Khovanskii, which I have not read). For more general schemes than this, the philosophy in most of the literature is to try to move away from the topological, path-based perspective and try to unify these topics in a more abstract setting (e.g. using Grothendieck’s functorial point of view). My aim here was slightly different, namely to try to recast Galois theory using the path-based framework. Probably this framework is nowhere near as general as the more category-theoretic approaches, but I found it to be helpful in allowing one to transfer topological intuition to more algebraic settings (as opposed to vice versa).
9 September, 2018 at 1:48 pm
Samuel Vidal
Hi, Sorry if I’m wrong, but I think there is a little typo in example 2. The nth cyclotomic field is an extension of degree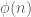 over
over 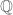 .
. is of degree 2. I really like the clarity of your blog. Regards
is of degree 2. I really like the clarity of your blog. Regards
For example
[Corrected, thanks – T.]
18 October, 2020 at 3:58 pm
Aidan Backus
I think there’s a typo in Theorem 4, iv; namely that $Gal(N/L) \cong Gal(M/L)/Gal(M/N)$ rather than $Gal(M/L)/Gal(N/L)$.
[Corrected, thanks – T.]