William Banks, Kevin Ford, and I have just uploaded to the arXiv our paper “Large prime gaps and probabilistic models“. In this paper we introduce a random model to help understand the connection between two well known conjectures regarding the primes , the Cramér conjecture and the Hardy-Littlewood conjecture:
Conjecture 1 (Cramér conjecture) If
is a large number, then the largest prime gap
in
is of size
. (Granville refines this conjecture to
, where
. Here we use the asymptotic notation
for
,
for
,
for
, and
for
.)
Conjecture 2 (Hardy-Littlewood conjecture) If
are fixed distinct integers, then the number of numbers
with
all prime is
as
, where the singular series
is defined by the formula
(One can view these conjectures as modern versions of two of the classical Landau problems, namely Legendre’s conjecture and the twin prime conjecture respectively.)
A well known connection between the Hardy-Littlewood conjecture and prime gaps was made by Gallagher. Among other things, Gallagher showed that if the Hardy-Littlewood conjecture was true, then the prime gaps with
were asymptotically distributed according to an exponential distribution of mean
, in the sense that
as for any fixed
. Roughly speaking, the way this is established is by using the Hardy-Littlewood conjecture to control the mean values of
for fixed
, where
ranges over the primes in
. The relevance of these quantities arises from the Bonferroni inequalities (or “Brun pure sieve“), which can be formulated as the assertion that
when is even and
when is odd, for any natural number
; setting
and taking means, one then gets upper and lower bounds for the probability that the interval
is free of primes. The most difficult step is to control the mean values of the singular series
as
ranges over
-tuples in a fixed interval such as
.
Heuristically, if one extrapolates the asymptotic (1) to the regime , one is then led to Cramér’s conjecture, since the right-hand side of (1) falls below
when
is significantly larger than
. However, this is not a rigorous derivation of Cramér’s conjecture from the Hardy-Littlewood conjecture, since Gallagher’s computations only establish (1) for fixed choices of
, which is only enough to establish the far weaker bound
, which was already known (see this previous paper for a discussion of the best known unconditional lower bounds on
). An inspection of the argument shows that if one wished to extend (1) to parameter choices
that were allowed to grow with
, then one would need as input a stronger version of the Hardy-Littlewood conjecture in which the length
of the tuple
, as well as the magnitudes of the shifts
, were also allowed to grow with
. Our initial objective in this project was then to quantify exactly what strengthening of the Hardy-Littlewood conjecture would be needed to rigorously imply Cramer’s conjecture. The precise results are technical, but roughly we show results of the following form:
Theorem 3 (Large gaps from Hardy-Littlewood, rough statement)
- If the Hardy-Littlewood conjecture is uniformly true for
-tuples of length
, and with shifts
of size
, with a power savings in the error term, then
.
- If the Hardy-Littlewood conjecture is “true on average” for
-tuples of length
and shifts
of size
for all
, with a power savings in the error term, then
.
In particular, we can recover Cramer’s conjecture given a sufficiently powerful version of the Hardy-Littlewood conjecture “on the average”.
Our proof of this theorem proceeds more or less along the same lines as Gallagher’s calculation, but now with allowed to grow slowly with
. Again, the main difficulty is to accurately estimate average values of the singular series
. Here we found it useful to switch to a probabilistic interpretation of this series. For technical reasons it is convenient to work with a truncated, unnormalised version
of the singular series, for a suitable cutoff ; it turns out that when studying prime tuples of size
, the most convenient cutoff
is the “Pólya magic cutoff“, defined as the largest prime for which
(this is well defined for ); by Mertens’ theorem, we have
. One can interpret
probabilistically as
where is the randomly sifted set of integers formed by removing one residue class
uniformly at random for each prime
. The Hardy-Littlewood conjecture can be viewed as an assertion that the primes
behave in some approximate statistical sense like the random sifted set
, and one can prove the above theorem by using the Bonferroni inequalities both for the primes
and for the random sifted set, and comparing the two (using an even
for the sifted set and an odd
for the primes in order to be able to combine the two together to get a useful bound).
The proof of Theorem 3 ended up not using any properties of the set of primes other than that this set obeyed some form of the Hardy-Littlewood conjectures; the theorem remains true (with suitable notational changes) if this set were replaced by any other set. In order to convince ourselves that our theorem was not vacuous due to our version of the Hardy-Littlewood conjecture being too strong to be true, we then started exploring the question of coming up with random models of
which obeyed various versions of the Hardy-Littlewood and Cramér conjectures.
This line of inquiry was started by Cramér, who introduced what we now call the Cramér random model of the primes, in which each natural number
is selected for membership in
with an independent probability of
. This model matches the primes well in some respects; for instance, it almost surely obeys the “Riemann hypothesis”
and Cramér also showed that the largest gap was almost surely
. On the other hand, it does not obey the Hardy-Littlewood conjecture; more precisely, it obeys a simplified variant of that conjecture in which the singular series
is absent.
Granville proposed a refinement to Cramér’s random model
in which one first sieves out (in each dyadic interval
) all residue classes
for
for a certain threshold
, and then places each surviving natural number
in
with an independent probability
. One can verify that this model obeys the Hardy-Littlewood conjectures, and Granville showed that the largest gap
in this model was almost surely
, leading to his conjecture that this bound also was true for the primes. (Interestingly, this conjecture is not yet borne out by numerics; calculations of prime gaps up to
, for instance, have shown that
never exceeds
in this range. This is not necessarily a conflict, however; Granville’s analysis relies on inspecting gaps in an extremely sparse region of natural numbers that are more devoid of primes than average, and this region is not well explored by existing numerics. See this previous blog post for more discussion of Granville’s argument.)
However, Granville’s model does not produce a power savings in the error term of the Hardy-Littlewood conjectures, mostly due to the need to truncate the singular series at the logarithmic cutoff . After some experimentation, we were able to produce a tractable random model
for the primes which obeyed the Hardy-Littlewood conjectures with power savings, and which reproduced Granville’s gap prediction of
(we also get an upper bound of
for both models, though we expect the lower bound to be closer to the truth); to us, this strengthens the case for Granville’s version of Cramér’s conjecture. The model can be described as follows. We select one residue class
uniformly at random for each prime
, and as before we let
be the sifted set of integers formed by deleting the residue classes
with
. We then set
with Pólya’s magic cutoff (this is the cutoff that gives
a density consistent with the prime number theorem or the Riemann hypothesis). As stated above, we are able to show that almost surely one has
and that the Hardy-Littlewood conjectures hold with power savings for up to
for any fixed
and for shifts
of size
. This is unfortunately a tiny bit weaker than what Theorem 3 requires (which more or less corresponds to the endpoint
), although there is a variant of Theorem 3 that can use this input to produce a lower bound on gaps in the model
(but it is weaker than the one in (3)). In fact we prove a more precise almost sure asymptotic formula for
that involves the optimal bounds for the linear sieve (or interval sieve), in which one deletes one residue class modulo
from an interval
for all primes
up to a given threshold. The lower bound in (3) relates to the case of deleting the
residue classes from
; the upper bound comes from the delicate analysis of the linear sieve by Iwaniec. Improving on either of the two bounds looks to be quite a difficult problem.
The probabilistic analysis of is somewhat more complicated than of
or
as there is now non-trivial coupling between the events
as
varies, although moment methods such as the second moment method are still viable and allow one to verify the Hardy-Littlewood conjectures by a lengthy but fairly straightforward calculation. To analyse large gaps, one has to understand the statistical behaviour of a random linear sieve in which one starts with an interval
and randomly deletes a residue class
for each prime
up to a given threshold. For very small
this is handled by the deterministic theory of the linear sieve as discussed above. For medium sized
, it turns out that there is good concentration of measure thanks to tools such as Bennett’s inequality or Azuma’s inequality, as one can view the sieving process as a martingale or (approximately) as a sum of independent random variables. For larger primes
, in which only a small number of survivors are expected to be sieved out by each residue class, a direct combinatorial calculation of all possible outcomes (involving the random graph that connects interval elements
to primes
if
falls in the random residue class
) turns out to give the best results.

37 comments
Comments feed for this article
26 August, 2019 at 11:17 am
thebirdreader
Why do you reveal the journal you submitted it to? More generally, what’s the policy around this?
26 August, 2019 at 11:33 am
domotorp
It’s nice of William Banks and Kevin Ford that they’ve helped you in uploading your own paper ;)
[Corrected, thanks – T.]
26 August, 2019 at 11:49 am
Anonymous
In the very first sentence, “my paper” should be “our paper”.
26 August, 2019 at 1:05 pm
Anonymous
Is it possible to improve the upper bound in (3) by optimizing “Polya magic cutoff” (perhaps by a slight modification of (2))?
26 August, 2019 at 2:12 pm
Terence Tao
Varying the cutoff significantly would vary the density of the set
significantly would vary the density of the set  , which would then also vary the lower and upper bounds we obtain for the largest gap (but the ratio between the upper and lower bounds would be essentially unchanged). The more precise version of (3) given in the paper involves the function
, which would then also vary the lower and upper bounds we obtain for the largest gap (but the ratio between the upper and lower bounds would be essentially unchanged). The more precise version of (3) given in the paper involves the function  , defined as the largest
, defined as the largest  for which it is possible to delete one residue class mod
for which it is possible to delete one residue class mod  from
from ![[0,y]](https://s0.wp.com/latex.php?latex=%5B0%2Cy%5D&bg=ffffff&fg=545454&s=0&c=20201002) for each prime
for each prime  and end up with at most
and end up with at most 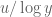 survivors. We basically show that the largest gap
survivors. We basically show that the largest gap  is almost surely asymptotic to
is almost surely asymptotic to  . On the other hand, the best known bounds on
. On the other hand, the best known bounds on  are
are
which is where the bounds (3) are coming from. We believe the lower bound here is closer to the truth, but improving the upper bound requires improving Iwaniec’s bound on the linear sieve, which is likely to be a very difficult problem (relating to breaking the notorious “parity barrier”). In an appendix to our paper we elaborate on the link with the parity problem by recording the folklore observation that a sufficiently strong Siegel zero can lead to a significant improvement in the lower bound for and hence for
and hence for  . So showing that the lower bound is sharp is at least as hard as ruling out Siegel zeroes.
. So showing that the lower bound is sharp is at least as hard as ruling out Siegel zeroes.
28 August, 2019 at 5:27 am
Anonymous
Is it necessary to use the same cutoff for both (upper and lower) bounds? Is it possible to optimize the cutoff for the lower bound and use another optimized cutoff for the upper bound?
26 August, 2019 at 3:03 pm
Two conjectures in one – The nth Root
[…] William Banks, Kevin Ford, and I have just uploaded to the arXiv my paper “Large prime gaps and probabilistic models“, submitted to Inventiones. In this paper we introduce a random model to help understand the connection between two well known conjectures regarding the primes {{mathcal P} := {2,3,5,dots}}, the Cramér conjecture and the Hardy-Littlewood conjecture: … (Terence Tao) […]
26 August, 2019 at 6:23 pm
Zachary Kyle Knutson
Research gate my sample 2 that was my idea…
27 August, 2019 at 6:19 am
Zachary Kyle Knutson
https://www.researchgate.net/publication/327477654_Sample_2_Update_J_Equation
27 August, 2019 at 6:28 am
Zachary Kyle Knutson
yall misunderstand that was to comment not lol to Mr.Terrance…
27 August, 2019 at 3:33 pm
Some Math News | Not Even Wrong
[…] too bad Pat didn’t live to see the latest from Terry Tao, who describes recent results which are related to old work of Gallagher’s by “Our […]
28 August, 2019 at 1:34 am
Vincent
Sorry can I ask a very basic question about the constant S(H) in the Hardy-Littlewood conjecture? I would have looked it up on Wikipedia but curiously the first HL-conjecture doesn’t have a page (while the probably-false second HL-conjecture does). As written here it seems to me that the constant equals 0 when all $h_i$ lie in the same congruence class mod $p$ for some $p$, e.g. when they are all even. That seems a bit strange in light of the twin prime conjecture. Conversely I would expect the constant to become 0 when for some $p$ we have$|H mod p| = p$, i.e. the $h_i$ together cover all congruence classes mod $p$, but in this case the contribution of the prime $p$ to the constant seems to be non-zero. Am I missing something obvious here? What is the rationale behind the product making up $S(H)$?
[Oops, there was a typo in the definition of the singular series in the blog post, which has now been fixed. -T]
28 August, 2019 at 8:26 pm
年轻的数学家
Dear Prof. Tao,
first of all, there seems to be a typo in the conclusion of thm. 1.5 (or do they also use the lower index for iteration?). Then, I wonder whether even stronger Hardy‒Littlewood-type estimates would imply even stronger bounds on . Also, what about upper bounds? Without having read the paper, the Bonferroni inequalities as stated above seem pretty symmetrical.
. Also, what about upper bounds? Without having read the paper, the Bonferroni inequalities as stated above seem pretty symmetrical.
30 August, 2019 at 7:52 am
Terence Tao
The lower index is indeed used for iteration (see the top of page 2).
Unfortunately, it appears that Hardy-Littlewood type conjectures can only be used to impose lower bounds on gaps, not upper bounds. To show that there is a prime gap of size at least H, it suffices to show that the number of in a given range such that the tuple
in a given range such that the tuple  is free of primes is positive; and this can in principle be done by the lower bound Bonferroni inequality and Hardy-Littlewood. But to show that all prime gaps have size at most H, one has to show that the number of
is free of primes is positive; and this can in principle be done by the lower bound Bonferroni inequality and Hardy-Littlewood. But to show that all prime gaps have size at most H, one has to show that the number of  for which the tuple
for which the tuple  is zero. One could only achieve this from an upper bound Bonferroni inequality if the upper bound was absolutely tight (no error term allowed at all), which is basically impossible from analytic number theory techniques (for instance, the Hardy-Littlewood conjectures contain an error term and are thus not usable for such a strategy).
is zero. One could only achieve this from an upper bound Bonferroni inequality if the upper bound was absolutely tight (no error term allowed at all), which is basically impossible from analytic number theory techniques (for instance, the Hardy-Littlewood conjectures contain an error term and are thus not usable for such a strategy).
One can also see this using the “redacted primes” test. One can “plant” a large gap in the primes by deleting an interval from the set of primes. For
from the set of primes. For  much smaller than the range
much smaller than the range  (e.g.
(e.g.  ), such a deletion will hardly make an impact on any of the Hardy-Littlewood conjectures (it will easily get absorbed into the error term). Thus these conjectures cannot prevent the creation of an extremely large gap.
), such a deletion will hardly make an impact on any of the Hardy-Littlewood conjectures (it will easily get absorbed into the error term). Thus these conjectures cannot prevent the creation of an extremely large gap.
28 August, 2019 at 8:38 pm
年轻的数学家
I’d also be interested in estimates for that would prove stronger bounds on
that would prove stronger bounds on  .
.
28 August, 2019 at 8:51 pm
年轻的数学家
I realise that according to the above, one would need to disprove the existence of Siegel zeroes. So I’m in fact asking for upper bounds in the event that both the Riemann hypothesis and strong Hardy‒Littlewood-type estimates are true.
30 August, 2019 at 5:54 am
Mefes
Good connection, but seems that landau’s problems are not provable though
30 August, 2019 at 2:03 pm
Anonymous
Dr.Tao, we can deduce the Hardy-Littlewood conjectures without using probabilistic models. You can see my article: https://lagrida.com/conjecture_k_uple.html
Where i prove
With : and
and 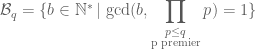 and
and  is the largest prime verify
is the largest prime verify 
30 August, 2019 at 2:06 pm
Anonymous
And f course
With is the number of distinct residues $\pmod p$ in $\mathcal{H}_k$.
is the number of distinct residues $\pmod p$ in $\mathcal{H}_k$.
30 August, 2019 at 3:25 pm
Anonymous
Hmm. On the largest gap or space, G(X), between consecutive primes less than or equal to large real X, I believe G(x) ≤ (log X)^2 is true according to an analysis involving the Prime Number Theorem and the average spacing between consecutive primes less than or equal to large real X.
Relevant Reference Link:
“LARGE GAPS BETWEEN CONSECUTIVE PRIME NUMBERS”,
https://www.math10.com/forum/viewtopic.php?f=63&t=8263
David Cole.
30 August, 2019 at 3:33 pm
Anonymous
Of course, the calculations are estimates/approximations within the known bounds of error associated with PNT/Riemann Prime-Counting Function for all large X… Our model/proof appears to be sound. David Cole.
30 August, 2019 at 3:38 pm
Anonymous
Remark: Riemann Hypothesis is true! David Cole. :-)
31 August, 2019 at 1:36 pm
Anonymous
Now I wonder why I even bother to visit this website/webpage… I always receive no positive feedback or worse. I will stop visiting this site in the future and this is my last comment and visit too. However, I do appreciate the information I gain here in the past. Thank you and goodbye. David Cole.
30 August, 2019 at 6:06 pm
anonymous
A possibly naive question: do you know if the constant 3/2 is optimal your Theorem 1.4, for the random model?
Also, does this model make predictions for the number of primes in short intervals much larger than log(x), along the lines of this paper of Montgomery and Soundararajan https://arxiv.org/pdf/math/0409258.pdf (e.g. Corollary 1 there)? I guess Theorem 1.3 of your paper allows one to directly reproduce Montgomery and Soundararajan’s computation for intervals of length up to exp(log(x)^{1/2}/loglog(x)), but for this model is there a more direct route that doesn’t pass through the computation of that paper, and is it feasible to consider short intervals larger than this?
30 August, 2019 at 6:32 pm
Terence Tao
We didn’t seriously try to optimise the exponent in Theorem 1.4, which arises basically from the second moment method and the Borel-Cantelli lemma. One could perhaps do a bit better by exploiting higher moments, but they become more difficult to compute.
I was planning to ask a graduate student to look into how what this model predicts for primes in short intervals; as we remark in Section 2.5, one does have the analogue of the Maier fluctuations in this model, but we didn’t quantify the size of these fluctuations precisely.
2 September, 2019 at 7:07 am
Mark
If you assume a Heath-Brown-type “conjecture” that the Hardy-Littlewood asymptotic holds with O(1) error term, can you deduce anything more about gaps?
2 September, 2019 at 7:42 am
Mark
I just noticed that the Heath-Brown’s “conjecture” already precludes the qualitative Hardy-Littlewood conjecture, as well as the Granville-Cramer gap prediction, so I’m not sure if there is much sense to be made from my question.
8 September, 2019 at 10:58 pm
Buzzman
Let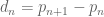 , then there exists
, then there exists  such that for
such that for  one obtains
one obtains  , with the implied constant depending on
, with the implied constant depending on 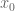 .
.
11 September, 2019 at 7:34 am
humble suggestion
I wonder if it might be worthwhile for Terry to hire an undergrad to periodically delete the nonsense in the comment sections. The posts about high profile results (and to a lesser extent, many other posts) tend to attract a lot of personal or crackpottish comments that are either off topic or nonsensical.
11 September, 2019 at 9:49 am
Kipperock
I think that this type of moderation would be welcome, both to the writer and the serious visitors.
This blog’s comment section is quite important, since, for example, in the comments about Prof. Tao’s books there are both errata and many super important explanations – I’m working through his book on measure theory rn and I just feel how invaluable a neat comment section is.
When reading other posts, expository or research – it would be very cool to see a neat comment section where serious discussions take place and are not spoiled by – sometimes dozens or more! – comments that are clearly.. not in the right neighborhood.
I guess I understand why the author refrains from flat out full time moderation – he’s got important research to do, teaching duties, two kids and a wife [this list is not written by order of importance :)))], and there probably are things I simply didn’t think of.
From my experience(see above, and take my word for it that it was me), it is also very, very tiring – since I would like to see certain comments completely gone, but others deserve at least an attempt at an answer.
I don’t even read the comments on other posts, in order to not get dragged down into the same mess of time and nerve consuming keyboard kung-fu..
Honestly I think this comment was just a very long way of saying “I agree”, since this comment section already had it’s way with me. I hope Prof. Tao would eventually accept your suggestion.
23 September, 2019 at 5:23 pm
Anonymous
Is it really a good idea to publish this where anyone can read it when it could help hackers break cryptography or evil governments conduct unjust wars. Even if new cryptographic software could be written people in third world countries could be greatly harmed and would not be able to update in time.
20 March, 2020 at 3:57 am
Zhang Tan
Proof of the Twin Prime Conjecture
Let $p_n$ be the nth prime number

Let $P_n$ be the first n prime numbers multiplied together
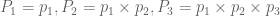
Arithmetic Progression
where
There always exist numbers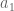 and
and  in
in  succh that
succh that 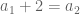 where
where 
Base Case in
in 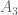
Induction Case
Let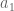 and
and  in
in 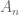 such that
such that  will propagate at least
will propagate at least 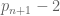 pairs of numbers which differs by
pairs of numbers which differs by  in
in 
There are a total of elements generated by arithmetic progression
elements generated by arithmetic progression 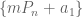 and out of all of the generated elements there is unique element
and out of all of the generated elements there is unique element  divisible by
divisible by 
There are a total of elements generated by arithmetic progression
elements generated by arithmetic progression  and out of all of the generated elements there is unique element
and out of all of the generated elements there is unique element  divisible by
divisible by 
When there are
there are 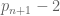 pairs of numbers
pairs of numbers  differs by
differs by  in
in 
When there are
there are 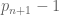 pairs of numbers
pairs of numbers  differs by
differs by  in
in 
Arithmetic Progression
If there exist an element in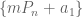 divisible by
divisible by  than in
than in  consecutive elements
consecutive elements  generated by arithmetic progression
generated by arithmetic progression 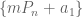 there exist unique element
there exist unique element  divisble by
divisble by 
Proof of twin prime conjecture by contradiction
For there to not exist two prime numbers which differs by
 in either
in either 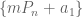 or $\{mP_n+a_2\}$
or $\{mP_n+a_2\}$
There must exist a non-prime number for every value of
All non-prime numbers greater than 1 in where
where  in
in 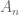 where
where  in relatively prime to
in relatively prime to 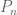 and less than
and less than 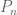 and
and 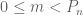 must be divisible by an odd number
must be divisible by an odd number  where
where 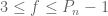
Removing pairs of numbers from where either
where either 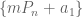 or
or  divisible by
divisible by 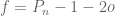 where
where 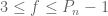
Consider consective elements
consective elements  generated by arithmetic progression
generated by arithmetic progression 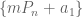 Assume there exist
Assume there exist  divisible by
divisible by  it is unique in these consecutive elements.
it is unique in these consecutive elements.
Consider consective elements
consective elements  generated by arithmetic progression
generated by arithmetic progression  Assume there exist
Assume there exist  divisible by
divisible by  it is unique in these consecutive elements.
it is unique in these consecutive elements.
Assume
Assume the remaining pairs not divisible by
pairs not divisible by  are consective.
are consective.
Taking the remaining consecutive pairs not divisible by
pairs not divisible by  remove pairs divisible by
remove pairs divisible by 
Consider consective elements
consective elements  generated by arithmetic progression
generated by arithmetic progression 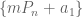 Assume there exist
Assume there exist  divisible by
divisible by  it is unique in these consecutive elements.
it is unique in these consecutive elements.
Consider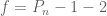 consective elements
consective elements  generated by arithmetic progression
generated by arithmetic progression  Assume there exist
Assume there exist  divisible by
divisible by  it is unique in these consecutive elements.
it is unique in these consecutive elements.
Assume
Assume the remaining pairs not divisible by
pairs not divisible by  are consective.
are consective.
Continue repeating until with all smaller odd numbers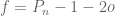 where
where  until
until 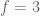
There must exist a prime number in and
and  where
where 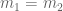 and
and 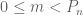
Therefore there are infinite number of prime numbers which differ by 2.
7 November, 2020 at 12:21 am
Thomas Pickett
My paper titled:
“Structure is found in Prime Numbers and Gaps are Unbounded as the Quantity of Twin and Cousin Primes Run Neck and Neck Through Infinity”
Addresses “Large Prime Gaps”.
It can be found at:
http://www.primealignmentmatrix.com
26 January, 2022 at 6:22 pm
Leigh
How does the GUE hypothesis ‘know’ that the prime counting function (or related counting functions) are piecewise constant? When you say “…we have the GUE hypothesis which appears to accurately model the zeta function, but does not capture such basic properties of the primes as the fact that the primes are all natural numbers,” it sounds like you are taking for granted that other distributions of the zeros will still lead to a sensible counting function. Or maybe I am reading too much into this statement.
27 January, 2022 at 8:27 am
Terence Tao
In fact none of the plausible models for the distribution for the zeta functions are able to detect the piecewise constancy of the prime counting function. This can be explained in terms of the uncertainty principle (see e.g., the discussion at the end of Section 2 of this blog post of mine): when trying to use the zeta function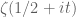 to understand sums like
to understand sums like  , the uncertainty principle tells us that
, the uncertainty principle tells us that
or by the chain rule
To see the piecewise constancy of the prime counting function, one has to resolve the spatial uncertainty down to unit scales, so we need , which by the uncertainty principle forces
, which by the uncertainty principle forces  . That is to say, we need information on the zeroes on an interval of length
. That is to say, we need information on the zeroes on an interval of length 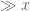 before we could even hope to detect this piecewise constancy. On the other hand, GUE and related models only cover intervals in
before we could even hope to detect this piecewise constancy. On the other hand, GUE and related models only cover intervals in  -space of length
-space of length 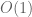 (or even
(or even  ) at best, and so have nowhere near the resolution to see these effects; as far as the GUE model (or any other local model for the zeroes) is concerned, the integers and primes may well be continuously distributed.
) at best, and so have nowhere near the resolution to see these effects; as far as the GUE model (or any other local model for the zeroes) is concerned, the integers and primes may well be continuously distributed.
It would be a major breakthrough if there was some new way to exploit the discrete nature of the integers and primes that would be visible on the zeta function side, thus circumventing this uncertainty principle barrier. The most obvious instance of this is the functional equation, which ultimately derives from the Poisson summation formula applied to the integers which one can view as a discrete subgroup of the reals. Some of the more advanced bounds on exponential sums related to the zeta function also rely more heavily on the arithmetic structure of the integers, but again not at anywhere near the resolution needed to say much about zeroes on the critical line (though they can help for instance with zero free regions and some zero density estimates, as well as subconvexity bounds).
27 January, 2022 at 7:25 pm
Leigh
OK that makes sense, thanks very much. I posted the above question on Math Stack Exchange (https://math.stackexchange.com/questions/4321777/riemanns-explicit-prime-counting-formula-how-is-it-piecewise-constant) a while ago, before posting it here. Do you mind if I copy your answer over there, with proper attribution? Or would you prefer to do so yourself if you do?
[Sure, any comment here is public and can be posted with attribution elsewhere. -T]
14 August, 2023 at 8:29 pm
The convergence of an alternating series of Erdos, assuming the Hardy–Littlewood prime tuples conjecture | What's new
[…] this obstacle, we take advantage of the random sifted model of the primes that was introduced in a paper of Banks, Ford, and myself. To model the primes in an interval such as with drawn randomly from say , we remove one random […]