Compactness and contradiction.
Terence TaoAmerican Mathematical Society
Publication Year: 2013
ISBN-10: 0-8218-9492-7
ISBN-13: 978-0-8218-9492-7
Last updated: Sep 1, 2023
This continues my series of books derived from my blog. The preceding books in this series were “Structure and Randomness“, “Poincaré’s legacies“, “An epsilon of room“, “An introduction to measure theory“, “Topics in random matrix theory“, and “Higher order Fourier analysis“.
A draft version of the MS can be found here.
Pre-errata (corrected in the published version):
- Page 78: In the first paragraph, “at least the” should be “at least one of the”. In the second paragraph, “generated by
” and “generated by
” should be “generated by
” and “generated by
” respectively. In the third paragraph, after the first sentence, add “We may take
to be a normal subgroup of
“. In the last paragraph, replace “cannot grow polynomially” by “cannot grow exponentially (as otherwise the number of subsums of
for
and
would grow exponentially in
, contradicting the polynomial growth hypothesis)”
- Page 79, footnote 12: replace the first sentence by “Proof: the algebraic integers
for natural number
have bounded degree and all Galois conjugates bounded, so the minimal polynomials have bounded integer coefficients and must thus repeat themselves after finitely many
.”
Errata:
- Page ???: In Section 1.3, “Wittingstein” should be “Wittgenstein”.
- Page 82: The first a in “dips below a on a” should be in math mode.
- Page 92: In the third display,
should be
.
- Page 94: “quarternionic” should be “quaternionic” (two occurrences).
- Page ???: In the paragraph before (3.17), (3.13) should be (3.12).
- Page 110: “considing” should be “considering”.
- Page ???: After equation (3.24),
should be
. Also, all occurrences of
in this section should be
for consistency.
- Page 131: in Section 3.10.2, at the end of the treatment of the non-transverse case, “the exponent of
here is positive” should be “the exponent of
here is negative”.
- Page 140: In Theorem 4.3.5, “there exists
” should be “there exists
“. In the definition of the shift
and the set
,
should be
respectively.
- Page 143: The à in Arzelà-Ascoli is missing.
- Page 220?: In Section 5.4.1, all occurrences of
should be
.
- Page 240: A, H should be in math mode in “determine how likely A would have occurred… under hypothesis H”. The second display should have
rather than >=. Just before and in the last display, the P(A_i) should have P in bold face. “infinity” should be
.
- Page 242: after display: “
” should be “
.
Thanks to Clément Caubel, Doron Lessure, Benjamin Sprung, Felix Voigtlaender, Bill Zajc, and an anonymous contributor for corrections.

16 comments
Comments feed for this article
1 July, 2011 at 10:49 am
Compactness and contradiction « What’s new
[…] of the last of my books based on my 2010 blog posts (and also my Google buzzes), entitled “Compactness and contradiction“. The PDF of this draft is available here. This is a somewhat assorted (and lightly […]
14 July, 2011 at 10:01 am
Tom
Small error (of a non-mathematical nature) on page 153
“each of the constants, operations, and relations as an elements, functions, and relations”
[Thanks, this will be corrected in the next version of the ms – T.]
18 August, 2016 at 9:35 am
BriefcaseJoe
This comment concerns the first subsection “1.1 Material implication”:
Interpreting “If A, then B” as saying “B is at least as true as A” sheds bright light on how one can prove the equivalence of two or more statements, that is, that they have the same truth value: Given “If A, then B” and “If B, then A”, we can infer that A is both at least and at most as true as B, allowing us to conclude that A and B are equivalent. In general, if we have proven a chain of implication of the form
then we can interpret this as saying that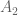 is at least as true as
is at least as true as 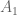 , that
, that 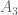 is at least as true as
is at least as true as 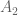 etc. and that *
etc. and that *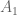 is at least as true as
is at least as true as 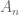 *. Thus, the statements
*. Thus, the statements 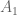 ,
, 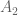 , …,
, …, 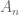 are equivalent.
are equivalent.
Indeed, until learning this way of looking at implications I didn’t fully understand proof by contrapositive (which is also evident when interpreting “If A, then B” as “B is at least as true as A” and “If not B, then not A” as “A is at least as false as B”) and the method of proving the equivalence of several statements discussed above. Does this mean that I am stupid? Or are there other ways of understanding these proof methods?
I am also wondering why this way of looking at implications isn’t mentioned in other text books or on the internet. Can you guys find an explanation of that?
10 December, 2016 at 9:06 am
Anonymous
Found a typo on page 4: “The early twentieth century philosopher Ludwig Wittingstein”. The austrian philosopher was called “Witt*gen*stein” instead.
At least this typo appears in the online version which can be found at
Click to access blog-book.pdf
[Typo added to errata, thanks – T.]
4 April, 2017 at 10:35 pm
Anonymous
P2, LINE 5, Is should be “If”
p13, correct comma “,”
p17, remove “it” this type of …..
p 18, correct Gdel to “Godel”
p24, proof of 1.10.11, we define G “as” or “to be”
[These are corrected in the printed version of the book – T.]
10 January, 2018 at 7:35 am
Thomas Arnold
Hey ho, after reading your thoughts on your no-self defeating object argument, I was just wondering whether you have looked into Graham Priest’s account of paraconsistent logics and what your thoughts on it are. Self-defeating objects appear at what he calls “the limits of thought” (or conception or expression, depending on the context) and are quite a common theme within philosophy (e.g. there is a debate about whether the world is such an object and should therefore be considered not to exist).
Now, Priest argues that these objects do in fact exist (and can be constructed and explained through what he calls “inclosure schema”, cf. Priest, Beyond the Limits of Thought, 2nd ed., 135) and simply show that we should reject classical logic as there can be ‘true contradictions’ (he and other proponents of dialethism have argued for this at length in several books, but cf https://plato.stanford.edu/entries/dialetheism/).
Most mathematicians I know simply reject this without argument, so I’m very interested in your thoughts on this.
24 December, 2020 at 9:31 am
Anonymous
Section 1.1 of the book says that “Material implication is not causal.” On the other hand, “if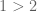 , then Riemann hypothesis is true” would not be considered as a proof.
, then Riemann hypothesis is true” would not be considered as a proof.
Should one say that material implication in a “proof” of a mathematical statement is supposed to be “causal”?
24 December, 2020 at 12:36 pm
Terence Tao
The material implication “if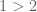 , then the Riemann hypothesis is true” is a true statement, but does not prove the Riemann hypothesis, since the antecedent is false. It is an example of a vacuously true statement – one which is technically true but unlikely to be of substantive value (though sometimes vacuous truths are still useful in mathematical arguments, e.g., as a convenient base case for an induction).
, then the Riemann hypothesis is true” is a true statement, but does not prove the Riemann hypothesis, since the antecedent is false. It is an example of a vacuously true statement – one which is technically true but unlikely to be of substantive value (though sometimes vacuous truths are still useful in mathematical arguments, e.g., as a convenient base case for an induction).
It is certainly good practice to structure one’s proofs so that the implications one uses in the arguments do have a causal connection from their hypotheses to their conclusions, though it is not strictly necessary; for instance a formal proof assistant will happily accept any valid material implication in a proof even if the conclusion has no obvious connection to the hypothesis. But even when a proof is aimed at human readers rather than computers, it can sometimes be useful to use acausal implications. For instance, if the proof needs to split into two cases X and Y, and there is a statement Z that holds in both cases, it may still be preferable to organize the argument to explicitly state the material implications “X implies Z” and “Y implies Z” to manage the two separate cases (e.g., if one wishes to add Z to a long list of conculsions in a proposition exploring the consequences of X, and also add Z to a long list of conclusions in a separate proposition exploring the consequences of Y), even though there is no causal relationship between Z and either X or Y. (In these sorts of cases though one often adds a remark after the implication to the effect that the conclusion Z holds under more general assumptions than just X or Y though, to avoid the reader drawing an incorrect conclusion regarding the causal relationship. One could also consider structuring the argument so that Z is established before one splits into the cases X and Y, though sometimes for notational or organisational reasons this is not always feasible or desirable.)
5 January, 2024 at 10:19 am
Anonymous
6 January, 2024 at 9:23 am
Anonymous
well, should be a natural number that encodes a sequence that encode the summation as usual. For sure,
should be a natural number that encodes a sequence that encode the summation as usual. For sure,  may be non-standard again.
may be non-standard again.
So, a few hours left. OK!
T.
27 February, 2024 at 1:34 am
Anonymous
7 March, 2024 at 7:14 pm
Anonymous
number, combination, finite function espcially Boolean, …
If one stayed away from those…
17 March, 2024 at 3:07 am
Anonymous
So, only arithmetization (IP=PSPACE) and probabilistically program checking are left to be read through. Note that even if they hold proven, that does not affect any protocol in use, for sure. Fame-only pursuit!
T. N.
19 March, 2024 at 3:23 am
Anonymous
It is called, they call it: function-restricted interactive protocol.
Input and every prover message/answer are all of the same length
and every prover message/answer are all of the same length  .
.
T. N.
5 April, 2024 at 11:28 pm
Anonymous
Green-Tao theorem is severely utilized in derandomization papers.
So is Szemeredi theorem.
TDN
11 March, 2024 at 10:10 pm
Anonymous
We will feature the paper
In Search of an Easy Witness: Exponential Time vs. Probabilistic Polynomial Time
in the last episode of our miniseries.