We continue the discussion of sieve theory from Notes 4, but now specialise to the case of the linear sieve in which the sieve dimension is equal to
, which is one of the best understood sieving situations, and one of the rare cases in which the precise limits of the sieve method are known. A bit more specifically, let
be quantities with
for some fixed
, and let
be a multiplicative function with
for all primes and some fixed
(we allow all constants below to depend on
). Let
, and for each prime
, let
be a set of integers, with
for
. We consider finitely supported sequences
of non-negative reals for which we have bounds of the form
for all square-free and some
, and some remainder terms
. One is then interested in upper and lower bounds on the quantity
The fundamental lemma of sieve theory (Corollary 19 of Notes 4) gives us the bound
This bound is strong when is large, but is not as useful for smaller values of
. We now give a sharp bound in this regime. We introduce the functions
by
where we adopt the convention . Note that for each
one has only finitely many non-zero summands in (6), (7). These functions are closely related to the Buchstab function
from Exercise 28 of Supplement 4; indeed from comparing the definitions one has
for all .
Exercise 1 (Alternate definition of
) Show that
is continuously differentiable except at
, and
is continuously differentiable except at
where it is continuous, obeying the delay-differential equations
for
, with the initial conditions
for
and
for
. Show that these properties of
determine
completely.
For future reference, we record the following explicit values of :
for .
We will show
Theorem 2 (Linear sieve) Let the notation and hypotheses be as above, with
. Then, for any
, one has the upper bound
if
is sufficiently large depending on
. Furthermore, this claim is sharp in the sense that the quantity
cannot be replaced by any smaller quantity, and similarly
cannot be replaced by any larger quantity.
Comparing the linear sieve with the fundamental lemma (and also testing using the sequence for some extremely large
), we conclude that we necessarily have the asymptotics
for all ; this can also be proven directly from the definitions of
, or from Exercise 1, but is somewhat challenging to do so; see e.g. Chapter 11 of Friedlander-Iwaniec for details.
Exercise 3 Establish the integral identities
and
for
. Argue heuristically that these identities are consistent with the bounds in Theorem 2 and the Buchstab identity (Equation (16) from Notes 4).
Exercise 4 Use the Selberg sieve (Theorem 30 from Notes 4) to obtain a slightly weaker version of (12) in the range
in which the error term
is worsened to
, but the main term is unchanged.
We will prove Theorem 2 below the fold. The optimality of is closely related to the parity problem obstruction discussed in Section 5 of Notes 4; a naive application of the parity arguments there only give the weak bounds
and
for
, but this can be sharpened by a more careful counting of various sums involving the Liouville function
.
As an application of the linear sieve (specialised to the ranges in (10), (11)), we will establish a famous theorem of Chen, giving (in some sense) the closest approach to the twin prime conjecture that one can hope to achieve by sieve-theoretic methods:
Theorem 5 (Chen’s theorem) There are infinitely many primes
such that
is the product of at most two primes.
The same argument gives the version of Chen’s theorem for the even Goldbach conjecture, namely that for all sufficiently large even , there exists a prime
between
and
such that
is the product of at most two primes.
The discussion in these notes loosely follows that of Friedlander-Iwaniec (who study sieving problems in more general dimension than ).
— 1. Optimality —
We first establish that the quantities appearing in Theorem 2 cannot be improved. We use the parity argument of Selberg, based on weight sequences
related to the Liouville function.
We argue for the optimality of ; the argument for
is similar and is left as an exercise. Suppose that there is
for which the claim in Theorem 2 is not optimal, thus there exists
such that
for as in that theorem, with
sufficiently large.
We will contradict this claim by specialising to a special case. Let be a large parameter going to infinity, and set
. We set
, then by Mertens’ theorem we have
. We set
to be the residue class
, thus (3) becomes
and (14) becomes
where .
Now let be a small fixed quantity to be chosen later, set
, and let
be the sequence
This is clearly finitely supported and non-negative. For any , we have
from the multiplicativity of . If
, then
, and then by the prime number theorem for the Liouville function (Exercise 41 from Notes 2, combined with Exercise 18 from Supplement 4) we have
(say), annd hence the remainder term in (15) is of size
As such, the error term in (16) may be absorbed into the
term, and so
Now we count the left-hand side. Observe that is supported on those numbers
that are the product of an odd number of primes
(possibly with repetition), in which case
. To be coprime to
, all these primes must be at least
; since we are restricting
, we thus must have
. The left-hand side of (18) may thus be written as
This expression may be computed using the prime number theorem:
Exercise 6 Show that the expression (19) is equal to
.
Since is continuous for
, we obtain a contradiction if
is sufficiently small.
Exercise 7 Verify the optimality of
in Theorem 2. (Hint: replace
by
in the above arguments.)
— 2. The linear sieve —
We now prove the forward direction of Theorem 2. Again, we focus on the upper bound (12), as the lower bound case is similar.
Fix . Morally speaking, the most natural sieve to use here is the (upper bound) beta sieve from Notes 4, with the optimal value of
, which for the linear sieve turns out to be
. Recall that this sieve is defined as the sum
where is the set of divisors
of
with
, such that
for all odd . From Proposition 14 of Notes 4 this is indeed an upper bound sieve; indeed we have
where is the set of divisors
of
with
, such that
for all odd . Now for the key heuristic point: if
lies in the support of
, then the sum in (20) mostly vanishes. Indeed, if
is such that
and
for some
and odd
, then one has
for some
that is not divisible by any prime less than
. On the other hand, from (21), (22) one has
and
which (morally) implies from the sieve of Erathosthenes that is prime, thus
and so
is not in the support of
. As such, we expect the upper bound sieve
to be extremely efficient on the support of
, which when combined with the analysis of the previous section suggests that this sieve should produce the desired upper bound (12).
One can indeed use this sieve to establish the required bound (12); see Chapter 11 of Friedlander-Iwaniec for details. However, for various technical reasons it will be convenient to modify this sieve slightly, by increasing the parameter to be slightly greater than
, and also by using the fundamental lemma to perform a preliminary sifting on the small primes.
We turn to the details. To prove (12) we may of course assume that is suitably small. It will be convenient to worsen the error
in (12) a little to
, since one can of course remove the logarithm by reducing
appropriately.
Set and
. By the fundamental lemma of sieve theory (Lemma 17 of Notes 4), one can find combinatorial upper and lower bound sieve coefficients
at sifting level
supported on divisors of
, such that
for all .
We will use the upper bound sieve as a preliminary sieve to remove the
for
; the lower bound sieve
plays only a minor supporting role, mainly to control the difference between the upper bound sieve
.
Next, we set , and let
be the upper bound beta sieve with parameter
on the primes dividing
up to level of distribution
. In other words,
consists of those divisors
of
with
such that
for all odd ; in particular,
for all
. By Proposition 14 of Notes 4, this is indeed an upper bound sieve for the primes dividing
:
Multiplying this with the second inequality in (24) (this is the method of composition of sieves), we obtain an upper bound sieve for the primes up to :
Multiplying this by and summing in
, we conclude that
Note that each product appears at most once in the above sum, and all such products are squarefree and at most
. Applying (3), we thus have
Thus to prove (12), it suffices to show that
for sufficiently large depending on
. Factoring out the
summation using (23), it thus suffices to show that
Now we eliminate the role of . From (1), (5) and Mertens’ theorem we have
for large enough. Also, if
, then
and all prime factors of
are at least
. Thus
has at most
prime factors, each of which are at least
. From (1) we then have
The contribution of the error term is then easily seen to be
for
large enough, and so we reduce to showing that
One can proceed here by evaluating the left-hand side directly. However, we will proceed instead by using the weight function from the previous section. More precisely, we will evaluate the expression
in two different ways, where is as before (but with the role of
now replaced by the function
). Firstly, since
, we see from the argument used to establish (17) that
(say). Since each appears at least once, we can thus write (26) as
which upon factoring the sum using (23) and Mertens’ theorem
Thus to verify (25), it will suffice to show that (26) is of the form
for sufficiently large.
To do this, we abbreviate (26) as
where are the sieves
By Proposition 14 of Notes 4, we can expand as
where for any ,
is the collection of all divisors
of
with
such that
for all with the same parity as
. For technical reasons, we will also impose the additional inequality
for all with the opposite parity as
; this follows from (30) when
, but is an additional constraint when
and
is even, but in the above identity
is odd, so this additional constraint is harmless. For similar reasons we impose the inequality
which follows from (30) or (31) except when , but then this inequality is automatic from our hypothesis
, which implies
if
is chosen small enough.
Inserting the identity (28), we can write (26) as
where
and
We first estimate . By(24), we can write
as the sum of
plus an error of size at most
(where we bound by
). The error may be rearranged as
which by (23) is of size for
small enough. As for the main term (33), we see from Exercise 6 (and the arguments preceding that exercise) that this term is equal to
for
sufficiently large. Thus, to obtain the desired approximation for (26), it will suffice to show that
Next, we establish an exponential decay estimate on the :
Lemma 8 For
sufficiently large depending on
, we have
for all
and some absolute constant
.
Proof: (Sketch) Note that if is in
, then
and all prime factors are at least
, thus we may assume without loss of generality that
.
We bound
Note that if lies in
, then
thanks to (29), (32). From this and the fundamental lemma of sieve theory we see (Exercise!) that
and so it will suffice to show that
By the prime number theorem, the left-hand side is bounded (Exercise!) by as
, where
and is the set of points
with
,
and such that
for all with the same parity as
, and
for all . It thus suffices to prove the bound
for all and some absolute constant
.
We use an argument from the book of Harman. Observe that vanishes for
, which makes the claim (35) routine for
(Exercise!) for
sufficiently large. We will now inductively prove (35) for all odd
. From the change of variables
, we obtain the identity
where when
is odd and
when
is even (Exercise!). In particular, if
is odd and (35) was already proven for
, then
One can check (Exercise!) that the quantity is maximised at
, where its value is less than
(in fact it is
) if
is small enough. As such, we obtain (35) if
is sufficiently close to
.
Finally, (35) for even follows from the odd
case (with a slightly larger choice of
) by one final application of (36).
Exercise 9 Fill in the steps marked (Exercise!) in the above proof.
In view of this lemma, the total contribution of with
for some sufficiently large
is acceptable. Thus it suffices to show that
whenever is odd.
By (24), we can write as
plus an error of size
Arguing as in the treatment of the term, we see from (23) that the error term is bounded by
as desired for large enough, since
and
. Thus it suffices to show that
If and
appear in the above sum, then we have
where
has no prime factor less than
, has an even number of prime factors, and obeys the bounds
thanks to (29). Note that (29) also gives , and thus (since
and
) we see that
if
is small enough and
is large enough. This forces
to either equal
, or be the product of two primes between
and
. The contribution of the
case is bounded by
, which is acceptable. As for the contribution of those
that are the product of two primes, the prime number theorem shows that there are at most
values of that can contribute to the sum, and so this contribution to
is at most
but by (34) the sum here is for
large enough, and the claim follows. This completes the proof of (12).
Exercise 10 Establish the lower bound (13) in Theorem 2. (Note that one can assume without loss of generality that
, which will now be needed to ensure (31) when
.)
— 3. Chen’s theorem —
We now prove Chen’s theorem for twin primes, loosely following the treatment in Chapter 25 of Friedlander-Iwaniec. We will in fact show the slightly stronger statement that
for sufficiently large , where
is the set of all numbers that are products of at most two primes, and
. Indeed, after removing the (negligible) contribution of those
that are powers of primes, this estimate would imply that there are infinitely many primes
such that
is the product of at most two primes, each of which is at least
.
Chen’s argument begins with the following simple lower bound sieve for :
Lemma 11 If
, then
Proof: If has no prime factors less than or equal to
, then
and the claim follows. If
has two or more factors less than or equal to
, then
and the claim follows. Finally, if
has exactly one factor less than or equal to
, then (as
) it must be of the form
for some
, or it is divisible by
for some
, and the claim again follows.
In view of this sieve (trivially managing the contribution of or of the case where
, and using the restriction of
to be coprime to
), it suffices to show that
for sufficiently large , where
and
We thus seek sufficiently good lower bounds on and sufficiently good upper bounds on
and
. As it turns out, the linear sieve, combined with the Bombieri-Vinogradov theorem, will give bounds on
with numerical constants that are sufficient for this purpose.
We begin with . We use the lower bound linear sieve, with
equal to the residue class
for all
, so that
is the residue class
. We approximate
where is the multiplicative function with
and
for
. From the Bombieri-Vinogradov theorem (Theorem 17 of Notes 3) we have
(say) if for some small fixed
. Applying the lower bound linear sieve (13), we conclude that
where
We can compute an asymptotic for :
as
, where
is the twin prime constant.
From (11) we have . Sending
slowly to zero, we conclude that
Now we turn to . Here we use the upper bound linear sieve. Let
be as before. For any
dividing
and
, we have
where and
are as previously. We apply the upper bound linear sieve (12) with level of distribution
, to conclude that
We sum over . Since
is at most
, and each number less than or equal to
has at most
prime factors, we have
The error term is thanks to (39). Since
, we thus have
for sufficiently large , thanks to Exercise 12. We can compute the sum using Exercise 37 of Notes 1, to obtain
which by (10) and sending slowly gives
A routine computation shows that
Finally, we consider , which is estimated by “switching” the sieve to sift out small divisors of
, rather than small divisors of
. Removing those
with
, as well as those
that are powers of primes, and then shifting
by
, we have
where is the finitely supported non-negative sequence
Here we are sifting out the residue classes , so that
.
The sequence has good distribution up to level
:
Proposition 13 One has
where
is as before, and
(say), with
as before.
Proof: Observe that the quantity in (42) is bounded above by
if the summand is to be non-zero. We now use a finer-than-dyadic decomposition trick similar to that used in the proof of the Bombieri-Vinogradov theorem in Notes 3 to approximate
as a combination of Dirichlet convolutions. Namely, we set
, and partition
(plus possibly a little portion to the right of
) into
consecutive intervals
each of the form
for some
. We similarly split
(plus possibly a tiny portion of
) into
intervals
each of the form
for some
. We can thus split
as
Observe that for each there are only
choices of
for which the summand can be non-zero. As such, the contribution of the diagonal case
can be easily seen to be absorbed into the
error, as can those cases where the product set
is not contained completely in
. If we let
be the set of triplets
obeying these properties, we can thus approximate
by
, where
is the Dirichlet convolution
From the general Bombieri-Vinogradov theorem (Theorem 16 of Notes 3) and the Siegel-Walfisz theorem (Exercise 64 of Notes 2) we see that
where
(say) and
This gives the claim with replaced by the quantity
; but by undoing the previous decomposition we see that this quantity is equal to
up to an error of
(say), and the claim follows.
Applying the upper bound sieve (12) (with sifting level ), we thus have
and hence by (10) and Exercise 12
for sufficiently large.
Note that
From the prime number theorem and Exercise 37 of Notes 1, we thus have
(In fact one also has a matching lower bound, but we will not need it here.) We thus conclude that
where
The left-hand side of (38) is then at least
One can calculate that , and the claim follows.
Exercise 14 Establish Chen’s theorem for the even Goldbach conjecture.
Remark 15 If one is willing to use stronger distributional claims on the primes than is provided by the Bombieri-Vinogradov theorem, then one can use a simpler sieve than Chen’s sieve to establish Chen’s theorem, but then the required distributional theorem will then either be conjectural or more difficult to establish than the Bombieri-Vinogradov theorem. See Chapter 25 of Friedlander-Iwaniec for further discussion.

23 comments
Comments feed for this article
29 January, 2015 at 4:16 pm
Eytan Paldi
It seems that in the RHS of (6)-(7), “ ” (in the integrands) should be “
” (in the integrands) should be “ “.
“.
[Corrected, thanks – T.]
29 January, 2015 at 5:32 pm
Eytan Paldi
Also in the line below (7).
[Corrected, thanks – T.]
29 January, 2015 at 7:41 pm
arch1
In the last two integrals preceding Exercise 9, the upper integration limit is misplaced.
[Corrected, thanks -T.]
29 January, 2015 at 7:50 pm
arch1
3 lines up from (37): we see from (23) *that the error*(?) is bounded by
[Corrected, thanks -T.]
1 February, 2015 at 8:46 am
Lior Silberman
In the proof of Chen’s Theorem, in the paragraph “We begin with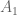 “,
“, 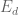 is said to be the class of -2 mod
is said to be the class of -2 mod  rather than mod
rather than mod  .
.
[Corrected, thanks – T.]
31 March, 2015 at 7:58 am
Karaskas
Just after the fragment “and the Siegel-Walfisz theorem (Exercise 64 of Notes 2) we see that [Formula] where” it should probably be log^{-10}x instead of log^{-100x}.
[Corrected, thanks – T.]
31 March, 2015 at 1:20 pm
Karaskas
Right now it’s log^{-10x} instead of log^{-10}x.
[Corrected, thanks – T.]
10 April, 2015 at 3:07 pm
Karaskas
Chen’s theorem section: shouldn’t it be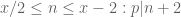 under the big sigma in the definition of
under the big sigma in the definition of  ? The same thing reappears a few lines later.
? The same thing reappears a few lines later.
Just after “Now we turn to “, what happens if p divides d?
“, what happens if p divides d?
[I was not able to locate this issue – T.]
11 April, 2015 at 12:43 am
Karaskas
In the same fragment it probably should be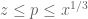 instead of
instead of  , shouldn’t it? That would also explain my last question.
, shouldn’t it? That would also explain my last question.
[Corrected, thanks – T.]
11 April, 2015 at 9:53 am
Karaskas
The issue wasn’t there anymore while I was writting about it. I think you had repaired it a few days before and I forgot to refresh the website. Sorry for the confusion.
issue wasn’t there anymore while I was writting about it. I think you had repaired it a few days before and I forgot to refresh the website. Sorry for the confusion.
By the way, thank you for writing posts about sieve theory. Some details and ideas are much easier for me to follow right now.
14 April, 2015 at 2:49 pm
Karaskas
The formula under “Applying the upper bound sieve” fragment: it should be instead of
instead of  in one place.
in one place.
[Corrected, thanks – T.]
15 December, 2015 at 5:04 pm
Karaskas
I have a little confusion: before the equation (40) we send {\varepsilon} to 0 slowly but in Theorem 2 we have “if {D} is sufficiently large depending on {\varepsilon, s, c}.” How should I understand this?
15 December, 2015 at 6:23 pm
Karaskas
It seems to me like we are using two different epsilons there. By the way, is it possible to relax conditions in Theorem 2 and let depend on z?
depend on z?
Theorem 2 also reminds me the Jurkat-Richert theorem, although we do not have any restriction on the sieve dimension. How do these two theorems are related to each other?
Sorry for doubling the post and using LaTeX wrongly in the previous one.
15 December, 2015 at 7:13 pm
Terence Tao
For any fixed choice of , the largeness condition on
, the largeness condition on  required for Theorem 2 will apply if
required for Theorem 2 will apply if  is large enough, thus
is large enough, thus
whenever is sufficiently large depending on
is sufficiently large depending on  (this allows for the o(1) errors to be absorbed into the
(this allows for the o(1) errors to be absorbed into the 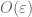 error). In particular, for any
error). In particular, for any 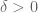 , one has
, one has
whenever is sufficiently large depending on
is sufficiently large depending on  (by choosing
(by choosing  appropriately depending on
appropriately depending on  ). This implies that
). This implies that
as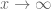 .
.
Another way to think about it as follows: if one has a bound of the form
as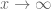 for any fixed choice of
for any fixed choice of  , then one automatically has the improvement
, then one automatically has the improvement
as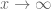 , by setting
, by setting  equal to a function of
equal to a function of  that goes to zero sufficiently slowly (slow enough so that the
that goes to zero sufficiently slowly (slow enough so that the  error in (1) still goes to zero even though
error in (1) still goes to zero even though  is now varying).
is now varying).
The Jurkat-Richert theorem has a slightly better error term replacing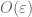 , and a slightly worse error term for the
, and a slightly worse error term for the 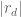 errors, but can easily be used as a substitute for Theorem 2 for the purpose of proving Chen’s theorem.
errors, but can easily be used as a substitute for Theorem 2 for the purpose of proving Chen’s theorem.
30 December, 2015 at 6:32 pm
Karaskas
I have one problem with Lemma 11. How do we rule out the numbers of the form , where
, where 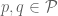 and
and  and
and 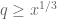 ?
?
I saw an another proof of Chen’s theorem in which the author (Nathanson, I guess) used the sum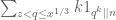 instead of
instead of  . By this trick we can easily avoid thinking about numbers which are not square-free.
. By this trick we can easily avoid thinking about numbers which are not square-free.
Are these two approaches equivalent in some easy way which I cannot see right now?
I would also like to thank you for your last answer.
[Oops, this case does need to be inserted, but it is easily dealt with (with , it contributes
, it contributes  from trivial estimates). -T.]
from trivial estimates). -T.]
10 July, 2019 at 2:51 pm
Anonymous
Why is of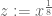 in Chen’s Theorem? Is it not the case that the closer
in Chen’s Theorem? Is it not the case that the closer  is to
is to 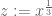 the better? I believe that using the same arguments and with same error term, one could set
the better? I believe that using the same arguments and with same error term, one could set 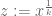 , where
, where  is the root of
is the root of  , i.e,
, i.e, 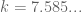 .
.
10 July, 2019 at 5:04 pm
Terence Tao
In this post I am not attempting to optimise the exponents in order to keep the exposition as clean as possible. I believe the text of Friedlander-Iwaniec contains further improvements to the exponent for , but I do not have the reference handy right now, and there may be further slight improvements in the literature.
, but I do not have the reference handy right now, and there may be further slight improvements in the literature.
UPDATE: Section 25.6 of Friedlander-Iwaniec allows to be as large as
to be as large as 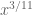 . It may be that further improvements are still possible beyond this exponent.
. It may be that further improvements are still possible beyond this exponent.
25 February, 2020 at 4:54 pm
Anonymous
Hi Prof Tao,
Just a quick question: why do we need eq. (31)? We seem to never use it in the proof. Apologies if I missed a clear usage of it.
26 February, 2020 at 4:43 pm
Terence Tao
(31) is needed to establish some cases of (32), which is then used in the proof of Lemma 8. (One could cut out the middle man and just impose (32), but this formalism is closer to the general beta-sieve formalism one sees for instance in the text of Iwaniec-Kowalski or Friedlander-Iwaniec.)
23 March, 2020 at 7:11 am
Michelangelo Mecozzi
A tiny detail: when we define and
and 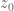 should the values be swapped? With the current values we have
should the values be swapped? With the current values we have 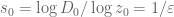 and I assume we want
and I assume we want 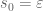 as in the proof.
as in the proof.
23 March, 2020 at 7:28 am
Michelangelo Mecozzi
My bad, actually we want that and it wouldn’t make sense to swap! I was working on the Exercise trying to show that the LHS of (34) is bounded by , this should be be
, this should be be  or I’m mistaken again? Doesn’t make any difference in the calculations…
or I’m mistaken again? Doesn’t make any difference in the calculations…
[Corrected, thanks – T.]
26 March, 2020 at 4:44 pm
Anonymous
Is it possible to get the following clarification: when you say (towards the end of the proof of the linear sieve) “Note that (29) also gives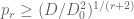 ” how can we deduce that?
” how can we deduce that?
[You are right, this is not the correct way to get a lower bound on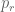 at this step. I will have to look at Friedlander-Iwaniec for the correct argument, but unfortunately due to the lockdown I will not be able to do so for a while. -T]
at this step. I will have to look at Friedlander-Iwaniec for the correct argument, but unfortunately due to the lockdown I will not be able to do so for a while. -T]
5 April, 2020 at 7:53 am
Terence Tao
I was finally able to retrieve my copy of Friedlander-Iwaniec. Theorem 2 is proven (in a stronger and more general form) as Theorem 11.12 from that paper. However the arguments are quite intricate, in particular the upper bounds on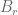 are proven recursively. I now vaguely remember finding an alternate approach (based on using the Selberg counterexample weights) to write the notes here, but as you pointed out the lower bounding of
are proven recursively. I now vaguely remember finding an alternate approach (based on using the Selberg counterexample weights) to write the notes here, but as you pointed out the lower bounding of 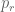 is incorrect. If one does compute what (29), (30) do give for lower bounds, they are more of the form
is incorrect. If one does compute what (29), (30) do give for lower bounds, they are more of the form 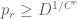 , thus the exponent degrades exponentially in
, thus the exponent degrades exponentially in  rather than linearly. This still gives satisfactory control on the
rather than linearly. This still gives satisfactory control on the 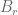 when
when  but now there is an intermediate region
but now there is an intermediate region  which is not currently covered by the above arguments. The issue is probably fixable, for instance by importing some of the recursive arguments from Friedlander-Iwaniec, but currently I will not have the time to address them and for now one should simply refer to Theorem 11.12 of Friedlander-Iwaniec for a proof of Theorem 2 in this post.
which is not currently covered by the above arguments. The issue is probably fixable, for instance by importing some of the recursive arguments from Friedlander-Iwaniec, but currently I will not have the time to address them and for now one should simply refer to Theorem 11.12 of Friedlander-Iwaniec for a proof of Theorem 2 in this post.