Kaisa Matomäki, Maksym Radziwill, Xuancheng Shao, Joni Teräväinen, and myself have just uploaded to the arXiv our preprint “Singmaster’s conjecture in the interior of Pascal’s triangle“. This paper leverages the theory of exponential sums over primes to make progress on a well known conjecture of Singmaster which asserts that any natural number larger than appears at most a bounded number of times in Pascal’s triangle. That is to say, for any integer
, there are at most
solutions to the equation
Our main result settles this conjecture in the “interior” region of the triangle:
Theorem 1 (Singmaster’s conjecture in the interior of the triangle) Ifand
is sufficiently large depending on
, there are at most two solutions to (1) in the region
and hence at most four in the region
Also, there is at most one solution in the region
To verify Singmaster’s conjecture in full, it thus suffices in view of this result to verify the conjecture in the boundary region
(or equivalentlyThe upper bound of two here for the number of solutions in the region (2) is best possible, due to the infinite family of solutions to the equation
coming from
The appearance of the quantity in Theorem 1 may be familiar to readers that are acquainted with Vinogradov’s bounds on exponential sums, which ends up being the main new ingredient in our arguments. In principle this threshold could be lowered if we had stronger bounds on exponential sums.
To try to control solutions to (1) we use a combination of “Archimedean” and “non-Archimedean” approaches. In the “Archimedean” approach (following earlier work of Kane on this problem) we view primarily as real numbers rather than integers, and express (1) in terms of the Gamma function as
Proposition 2 Let, and suppose
is sufficiently large depending on
. If
is a solution to (1) in the left half
of Pascal’s triangle, then there is at most one other solution
to this equation in the left half with
Again, the example of (4) shows that a cluster of two solutions is certainly possible; the convexity argument only kicks in once one has a cluster of three or more solutions.
To finish the proof of Theorem 1, one has to show that any two solutions to (1) in the region of interest must be close enough for the above proposition to apply. Here we switch to the “non-Archimedean” approach, in which we look at the
-adic valuations
of the binomial coefficients, defined as the number of times a prime
divides
. From the fundamental theorem of arithmetic, a collision
A key idea in our approach is to view this condition (6) statistically, for instance by viewing as a prime drawn randomly from an interval such as
for some suitably chosen scale parameter
, so that the two sides of (6) now become random variables. It then becomes advantageous to compare correlations between these two random variables and some additional test random variable. For instance, if
and
are far apart from each other, then one would expect the left-hand side of (6) to have a higher correlation with the fractional part
, since this term shows up in the summation on the left-hand side but not the right. Similarly if
and
are far apart from each other (although there are some annoying cases one has to treat separately when there is some “unexpected commensurability”, for instance if
is a rational multiple of
where the rational has bounded numerator and denominator). In order to execute this strategy, it turns out (after some standard Fourier expansion) that one needs to get good control on exponential sums such as
A modification of the arguments also gives similar results for the equation
where
Theorem 3 Ifand
is sufficiently large depending on
, there are at most two solutions to (7) in the region
Again the upper bound of two is best possible, thanks to identities such as

31 comments
Comments feed for this article
7 June, 2021 at 6:48 pm
William Verreault
What a coincidence, I was a coauthor on a paper that only recently appeared in Integers on Singmaster’s conjecture, called ”Repetitions of Multinomial Coefficients and a Generalization of Singmaster’s Conjecture”.
It is #A34 on Integers 2021 page: http://math.colgate.edu/~integers/current.html
It’d be interesting to see how these ideas hold up in higher dimensions!
8 June, 2021 at 7:41 am
Terence Tao
Thanks for the reference! It does seem plausible that the methods will extend to multinomial equations such as in the interior of the simplex
in the interior of the simplex 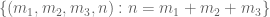 . It is tempting for instance to work in the region
. It is tempting for instance to work in the region 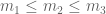 and express
and express  as an analytic function
as an analytic function 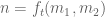 of
of 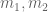 for a given
for a given  . If one can establish some convexity bounds on this function
. If one can establish some convexity bounds on this function  then the Archimedean arguments should largely go through (though now clusters can have three solutions instead of two). The types of correlations we compute in the non-Archimedean arguments would also be computable in the multinomial case, but the case analysis is likely to be more complicated. Still one should be able to get some partial results at least in this case (optimistically one could hope for an upper bound of three solutions in the interior of the simplex when
then the Archimedean arguments should largely go through (though now clusters can have three solutions instead of two). The types of correlations we compute in the non-Archimedean arguments would also be computable in the multinomial case, but the case analysis is likely to be more complicated. Still one should be able to get some partial results at least in this case (optimistically one could hope for an upper bound of three solutions in the interior of the simplex when 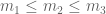 , and thus at most
, and thus at most  solutions without the order restriction, but there may be technical issues preventing one from getting this far).
solutions without the order restriction, but there may be technical issues preventing one from getting this far).
15 June, 2021 at 12:24 pm
William Verreault
That sounds good, I’ll have to try to work it out!
Have you looked at whether one can improve these results (and possibly prove Singmaster’s conjecture) conditionally on other various conjectures (e.g. GRH to get better exponential sum estimates, bounds on gaps between primes to modify the regions where you work, possibly abc conjecture, etc.)?
16 June, 2021 at 10:01 am
Terence Tao
This is briefly discussed in the footnote on page 2. The main thing that is needed in our arguments are estimates of the form
for various large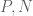 (this is roughly the same as asking that the fractional parts
(this is roughly the same as asking that the fractional parts 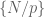 for prime
for prime  are uniformly distributed). [Actually for technical reasons (involving the need to also control prime powers
are uniformly distributed). [Actually for technical reasons (involving the need to also control prime powers 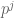 ) we work with a slightly shorter interval than
) we work with a slightly shorter interval than ![[P,2P]](https://s0.wp.com/latex.php?latex=%5BP%2C2P%5D&bg=ffffff&fg=545454&s=0&c=20201002) and need a slightly more general phase and slightly stronger error terms, but never mind these complications for now.] The estimates of Vinogradov basically let us get something like this as long as
and need a slightly more general phase and slightly stronger error terms, but never mind these complications for now.] The estimates of Vinogradov basically let us get something like this as long as 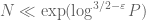 , but pseudorandomness heuristics predict a much larger range of
, but pseudorandomness heuristics predict a much larger range of  such as
such as 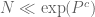 for some
for some  (perhaps even
(perhaps even  arbitrarily close to 1), which would lead to widening the applicability of our results to something like
arbitrarily close to 1), which would lead to widening the applicability of our results to something like  . In comparison, the Riemann hypothesis would (morally, at least) give results of the form
. In comparison, the Riemann hypothesis would (morally, at least) give results of the form
for such a wide range of , which certainly looks similar, but we could not obtain a direct connection between the two types of estimates.
, which certainly looks similar, but we could not obtain a direct connection between the two types of estimates.
22 August, 2021 at 5:55 am
思
Hello,professor. I am a Chinese student about to enter freshman year. These days, I think about the “3N + 1” conjecture. I think I should prove it. I wonder if you could have a look. If you can, please reply me! esteem it a favor!
8 June, 2021 at 2:21 am
Anonymous
Typo in the formula after (5): the sum should be over $P \le p \le P + P \log^{-100} P$.
[Corrected, thanks – T.]
8 June, 2021 at 4:44 am
Simple unsolved math problem, 5 | Yet Another Mathblog
[…] Xuancheng Shao, Joni Teräväinen, and Terrance Tao solved the conjecture below recently (see T. Tao’s blog post with the link to the paper and a […]
8 June, 2021 at 5:20 pm
Anonymous
Is it possible to extend these results (beyond binomial coefficients) for a larger class of functions (having certain regularity properties and sufficiently fast growth rate)?
(having certain regularity properties and sufficiently fast growth rate)?
9 June, 2021 at 9:12 am
Terence Tao
Such hypotheses would suffice for the “Archimedean” parts of the argument, but for the “non-Archimedean” parts one needs to know information about the prime factorisation of . For instance, a basic property about the prime factorisation of
. For instance, a basic property about the prime factorisation of  for
for 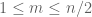 is that this binomial coefficient is divisible by every prime between
is that this binomial coefficient is divisible by every prime between  and
and  , but not by any prime larger than
, but not by any prime larger than  . This fact alone is already enough to establish non-collision
. This fact alone is already enough to establish non-collision 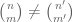 for a reasonable number of pairs
for a reasonable number of pairs  ; the argument we employ evolved from various attempts to try to generalise this type of argument (which already appears in an early work on this problem by Abbott, Erdos, and Hansen).
; the argument we employ evolved from various attempts to try to generalise this type of argument (which already appears in an early work on this problem by Abbott, Erdos, and Hansen).
12 June, 2021 at 7:11 pm
Anonymous
Non twin prime
After adding 1 and 3 to each natural number in the natural number set n, a pair of new numbers with 1 and 3 bits can be formed. If the pair of numbers are twin primes, the corresponding elements in the n set are put into the a set, otherwise they are put into the B set. For example, after adding the numbers 1 and 3 to the number “4” in the n set, two new numbers 41 and 43 are formed, which are a pair of twin prime numbers, then “4” is put into the a set.
For example, natural numbers within 10 can be divided into two categories as follows:
Class 1: there are four numbers, specifically 1, 4, 7 and 10. According to this rule, they should be put into a set,
Class 2: there are six numbers: 2, 3, 5, 6, 8, 9. According to this rule, they should be put into b set.
Obviously, a and B sets complement each other and refer to four pairs of twin primes, twin primes and six pairs of non twin primes with 1 and 3 in natural number 109 respectively.
Can we say that the elements in B set are “non twin primes” and complement of twin primes?
Here, we only study the twin prime numbers 11-13 and 41-43, which are 1 and 3.
8 June, 2021 at 11:19 pm
Anonymous
How can I read the inequalities if e.g. ? For Eq. (2) one gets
? For Eq. (2) one gets  which is…weird.
which is…weird.
9 June, 2021 at 6:39 am
Aunonymous
I mean, what he said is true. The interval is just empty.
9 June, 2021 at 11:43 am
Anonymous
Maksym’s webpage is mis-linked.
[Corrected, thanks – T.]
9 June, 2021 at 3:01 pm
Singmaster and Pascal – The nth Root
[…] Kaisa Matomäki, Maksym Radziwill, Xuancheng Shao, Joni Teräväinen, and myself have just uploaded to the arXiv our preprint “Singmaster’s conjecture in the interior of Pascal’s triangle“. This paper leverages the theory of exponential sums over primes to make progress on a well known conjecture of Singmaster which asserts that any natural number larger than {1} appears at most a bounded number of times in Pascal’s triangle. … (Terry Tao) […]
10 June, 2021 at 1:07 am
Singmaster’s conjecture – SPP 2026
[…] learned about this conjecture by a blog post of Terence Tao on his own blog. There he reported on recent progress on this conjecture […]
10 June, 2021 at 7:52 am
Antoine Deleforge
Really nice work! I noticed one small inconsistency between the elementary examples in your paper and the ones given on the Wikipedia page on Singmaster’s conjecture (https://en.wikipedia.org/wiki/Singmaster%27s_conjecture): you give (52, 22, 3) while the wikipedia page seems to give (56, 22, 3). Do you know which one is correct?
[Thanks for locating this typo; it will be corrected in the next version of the ms. -T]
11 June, 2021 at 10:42 am
Anonymous
It is not clear from the statement of the conjecture (both here and in the arXiv paper) if the number of solutions to (1) is dependent on (i.e.
(i.e. 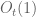 ) or is uniformly bounded wrt
) or is uniformly bounded wrt  .
.
[Uniformly bounded in , otherwise we would have used
, otherwise we would have used 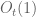 as in Section 1.5 of the paper. -T]
as in Section 1.5 of the paper. -T]
13 June, 2021 at 1:44 am
Anonymous
The upper bound of two here for the number of solutions in the region (8)
should be changed to
The upper bound of two here for the number of solutions in the region (2)
perhaps?
[Corrected, thanks – T.]
13 June, 2021 at 4:31 am
Anonymous
I don’t believe any random ways,
15 June, 2021 at 5:02 pm
JSE
The part of the argument where a set of integer points on a real-analytic subvariety (in this case three points on a curve) can’t cluster together too closely because the area of the simplex they determine would be too small (but also nonzero) feels reminiscent of the work of Bombieri and Pila, which also gives bounds for the number of integer points on a curve with bounded coordinates, those bounds being uniform in the curve in the same way your bounds are uniform in t. Did you have this stuff in mind and do you think there’s any relation?
16 June, 2021 at 10:06 am
Terence Tao
Nice observation! We were not directly inspired by the Bombieri–Pila determinant method (the argument we use comes instead from a paper of Kane) but now that you mention it, there is definitely a similarity that we will mention in the next revision of the ms.
This does raise the possibility though that it might be possible to use the determinant method (in either the Archimedean or non-Archimedean form) to improve the upper bound for the total number of solutions to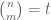 ; the best bound currently is
; the best bound currently is  , due to Kane, and relying primarily on derivative estimates for this real-analytic curve. There the problem comes more from the edge of Pascal’s triangle than the interior, and I don’t think the rest of the methods in our paper are directly useful for this problem, but perhaps it is something for an expert in the determinant method to take a look at. (The key difficulty would be to get good quantitative estimates on the number of intersection points between the solution set
, due to Kane, and relying primarily on derivative estimates for this real-analytic curve. There the problem comes more from the edge of Pascal’s triangle than the interior, and I don’t think the rest of the methods in our paper are directly useful for this problem, but perhaps it is something for an expert in the determinant method to take a look at. (The key difficulty would be to get good quantitative estimates on the number of intersection points between the solution set 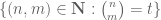 and an algebraic curve of a given degree.)
and an algebraic curve of a given degree.)
15 June, 2021 at 5:12 pm
Aditya Guha Roy
Reblogged this on Aditya Guha Roy's weblog.
17 June, 2021 at 3:35 pm
duck_master
In retrospect, the idea of comparing the valuations for a *random* prime number is extremely clever. (I had thought about comparing valuations before; however, I initially tried studying , but I gave up because this has to do with base-2, base-3, base-5, etc. expansions, and these don’t generally relate simply to each other.)
, but I gave up because this has to do with base-2, base-3, base-5, etc. expansions, and these don’t generally relate simply to each other.)
Also, to simplify the proof: you could sample your choice of for the application of valuation-comparison with probability
for the application of valuation-comparison with probability  . On the “back-end” (the actual computation of the correlations), this gets rid of the now-unnecessary summation-by-parts on (in the latest version as of the time of writing) the top of page 22, which serves as the transition from naïve uniform sampling to my proposed version of sampling; on the “front-end” (the application of the correlations to restricting solutions of
. On the “back-end” (the actual computation of the correlations), this gets rid of the now-unnecessary summation-by-parts on (in the latest version as of the time of writing) the top of page 22, which serves as the transition from naïve uniform sampling to my proposed version of sampling; on the “front-end” (the application of the correlations to restricting solutions of 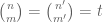 ), this is perfectly okay because the failure probability of the identity is at most
), this is perfectly okay because the failure probability of the identity is at most  and the difference of the two sides in cases of failure is at most
and the difference of the two sides in cases of failure is at most  anyways, which introduces a perfectly-manageable error term of
anyways, which introduces a perfectly-manageable error term of  for the correlation equation.
for the correlation equation.
19 June, 2021 at 10:20 am
Terence Tao
Yes, these two sampling methods are basically equivalent and which one to use is mostly a matter of personal preference. The weighting is often more convenient in proving the estimates, but the naive weighting involving primes drawn at random is conceptually simpler and is often the formulation used in describing many theorems or conjectures about the primes.
is often more convenient in proving the estimates, but the naive weighting involving primes drawn at random is conceptually simpler and is often the formulation used in describing many theorems or conjectures about the primes.
18 June, 2021 at 12:00 pm
William Verreault
I would like to know where your motivation to work on Singmaster’s conjecture came from since it is not as well-known as other conjectures. Did it come from your co-authors? If so, what was their motivation to look at Singmaster’s conjecture? Were you motivated by something else first?
I know you said in another comment that these arguments evolved from trying to generalize arguments that use the prime factorization of , but did you find Kane’s ”archimedean” approach first and then figured out a way to improve the proof with non-archimedean arguments?
, but did you find Kane’s ”archimedean” approach first and then figured out a way to improve the proof with non-archimedean arguments?
19 June, 2021 at 10:49 am
Terence Tao
The five of us are working on a related project involving exponential sums over primes that we hope to finalise soon. At one point in that project, one of us realised a possible connection of our work to Singmaster’s conjecture, although it turned out in the end that we were able to get our results using just the standard Vinogradov estimates on exponential sums on primes rather than the ones we have been working on.
The connection between equidistribution properties over primes (or equivalently, exponential sums over primes) and Singmaster started with the basic observation that when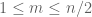 , the binomial coefficient
, the binomial coefficient  is divisible by every prime between
is divisible by every prime between  and
and  , but not divisible by any prime larger than
, but not divisible by any prime larger than  . This is already enough to get decent results in the regime
. This is already enough to get decent results in the regime  (and was already exploited in an old paper of Abbott, Erdos, and Hansen), though for much smaller values of
(and was already exploited in an old paper of Abbott, Erdos, and Hansen), though for much smaller values of  this is less useful as the interval
this is less useful as the interval ![[n-m+1,n]](https://s0.wp.com/latex.php?latex=%5Bn-m%2B1%2Cn%5D&bg=ffffff&fg=545454&s=0&c=20201002) is too short to provably contain primes. Our starting point was then the heuristic variant of the above observation (say in the region
is too short to provably contain primes. Our starting point was then the heuristic variant of the above observation (say in the region  to avoid dealing with contributions of powers of primes) that
to avoid dealing with contributions of powers of primes) that  tended to be divisible by most primes in
tended to be divisible by most primes in ![[m,(1+\varepsilon) m]](https://s0.wp.com/latex.php?latex=%5Bm%2C%281%2B%5Cvarepsilon%29+m%5D&bg=ffffff&fg=545454&s=0&c=20201002) but very few primes in
but very few primes in ![[(1-\varepsilon) m,m]](https://s0.wp.com/latex.php?latex=%5B%281-%5Cvarepsilon%29+m%2Cm%5D&bg=ffffff&fg=545454&s=0&c=20201002) , and this could be used to separate
, and this could be used to separate  from
from  , for instance if
, for instance if  . This idea then went through several iterations and refinements (for instance we mostly started with first moment estimates on fractional parts
. This idea then went through several iterations and refinements (for instance we mostly started with first moment estimates on fractional parts 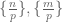 and only later realised the utility of second moment estimates, i.e., correlation estimates) until reaching the current form.
and only later realised the utility of second moment estimates, i.e., correlation estimates) until reaching the current form.
19 June, 2021 at 6:29 pm
Richard
Thanks for both this comment and your reponse. It’s so interesting to glimpse insights into these (partial? Partial? PARTIAL? More than I could ever dream of!) results are realised, and how collaborations alight on them.
21 June, 2021 at 11:28 am
William Verreault
Thank you for the very detailed answer. It is always nice to have insight into where these new ideas come from!
This basic observation on the divisibility of makes me think that these new techniques can’t help when considering the similar question on solutions to n!m!=t (as studied by Kane using the same Archimedean arguments in ”On the number of ways of writing t as a product of factorials”). Is that right?
makes me think that these new techniques can’t help when considering the similar question on solutions to n!m!=t (as studied by Kane using the same Archimedean arguments in ”On the number of ways of writing t as a product of factorials”). Is that right?
To be more precise, he proved that the of the number of solutions to the previous equation is 6, but conjectured it is the maximum, and I would find it interesting to see if this can be improved using your ideas (whether by obtaining effective bounds on ”large values of t” that could help numerically verify this conjecture or by obtaining similar results for n_1!…n_k!=t).
of the number of solutions to the previous equation is 6, but conjectured it is the maximum, and I would find it interesting to see if this can be improved using your ideas (whether by obtaining effective bounds on ”large values of t” that could help numerically verify this conjecture or by obtaining similar results for n_1!…n_k!=t).
21 June, 2021 at 5:48 pm
Terence Tao
For the equation studied by Kane, as well as the similar equation
studied by Kane, as well as the similar equation 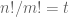 studied in the last section of our paper, it seems the
studied in the last section of our paper, it seems the  -valuation
-valuation  already gives quite a lot of information; for
already gives quite a lot of information; for  we experimented with working with more general
we experimented with working with more general  -valuations
-valuations  as we did for
as we did for 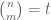 , but the information we could extract from the other valuations was not as strong as what one could already get using
, but the information we could extract from the other valuations was not as strong as what one could already get using  . Similarly, in Kane’s paper it seems the
. Similarly, in Kane’s paper it seems the 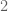 -valuation already pinpoints
-valuation already pinpoints 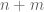 to an accuracy of
to an accuracy of  , which looks much better than what one could hope to accomplish through other valuations.
, which looks much better than what one could hope to accomplish through other valuations.
27 June, 2021 at 8:24 am
Healthy Social Media, Secrets of Pascal’s Triangle and Venus’ Tectonics – Phil Beaudoin
[…] “ I have no idea which number it is, but it probably appears infinitely many times. ” Well, thanks to Terrence Tao and Waverly, I learned this week about the Singmaster’s conjecture which says that no number […]
30 June, 2021 at 7:15 am
Glenn Wouda
Dear professor Tao, I am trying to get to the errata for your book “Analysis I (third edition)” but the page https://terrytao.wordpress.com/books/analysis-i/ freezes and there is a pop-up saying that the the page is waiting to load.
I have tried on several occasions and also with several different browsers but the problem persists.
Having the errata available would help me a lot while reading and studying your book.
Thanks in advance
[I have changed the comment settings to only display the most recent 50 comments, which seems to alleviate this loading issue -T.]