We have seen in previous notes that the operation of forming a Dirichlet series
or twisted Dirichlet series
is an incredibly useful tool for questions in multiplicative number theory. Such series can be viewed as a multiplicative Fourier transform, since the functions and
are multiplicative characters.
Similarly, it turns out that the operation of forming an additive Fourier series
where lies on the (additive) unit circle
and
is the standard additive character, is an incredibly useful tool for additive number theory, particularly when studying additive problems involving three or more variables taking values in sets such as the primes; the deployment of this tool is generally known as the Hardy-Littlewood circle method. (In the analytic number theory literature, the minus sign in the phase
is traditionally omitted, and what is denoted by
here would be referred to instead by
,
or just
.) We list some of the most classical problems in this area:
- (Even Goldbach conjecture) Is it true that every even natural number
greater than two can be expressed as the sum
of two primes?
- (Odd Goldbach conjecture) Is it true that every odd natural number
greater than five can be expressed as the sum
of three primes?
- (Waring problem) For each natural number
, what is the least natural number
such that every natural number
can be expressed as the sum of
or fewer
powers?
- (Asymptotic Waring problem) For each natural number
, what is the least natural number
such that every sufficiently large natural number
can be expressed as the sum of
or fewer
powers?
- (Partition function problem) For any natural number
, let
denote the number of representations of
of the form
where
and
are natural numbers. What is the asymptotic behaviour of
as
?
The Waring problem and its asymptotic version will not be discussed further here, save to note that the Vinogradov mean value theorem (Theorem 13 from Notes 5) and its variants are particularly useful for getting good bounds on ; see for instance the ICM article of Wooley for recent progress on these problems. Similarly, the partition function problem was the original motivation of Hardy and Littlewood in introducing the circle method, but we will not discuss it further here; see e.g. Chapter 20 of Iwaniec-Kowalski for a treatment.
Instead, we will focus our attention on the odd Goldbach conjecture as our model problem. (The even Goldbach conjecture, which involves only two variables instead of three, is unfortunately not amenable to a circle method approach for a variety of reasons, unless the statement is replaced with something weaker, such as an averaged statement; see this previous blog post for further discussion. On the other hand, the methods here can obtain weaker versions of the even Goldbach conjecture, such as showing that “almost all” even numbers are the sum of two primes; see Exercise 34 below.) In particular, we will establish the following celebrated theorem of Vinogradov:
Theorem 1 (Vinogradov’s theorem) Every sufficiently large odd number
is expressible as the sum of three primes.
Recently, the restriction that be sufficiently large was replaced by Helfgott with
, thus establishing the odd Goldbach conjecture in full. This argument followed the same basic approach as Vinogradov (based on the circle method), but with various estimates replaced by “log-free” versions (analogous to the log-free zero-density theorems in Notes 7), combined with careful numerical optimisation of constants and also some numerical work on the even Goldbach problem and on the generalised Riemann hypothesis. We refer the reader to Helfgott’s text for details.
We will in fact show the more precise statement:
Theorem 2 (Quantitative Vinogradov theorem) Let
be an natural number. Then
The implied constants are ineffective.
We dropped the hypothesis that is odd in Theorem 2, but note that
vanishes when
is even. For odd
, we have
Unfortunately, due to the ineffectivity of the constants in Theorem 2 (a consequence of the reliance on the Siegel-Walfisz theorem in the proof of that theorem), one cannot quantify explicitly what “sufficiently large” means in Theorem 1 directly from Theorem 2. However, there is a modification of this theorem which gives effective bounds; see Exercise 32 below.
Exercise 4 Obtain a heuristic derivation of the main term
using the modified Cramér model (Section 1 of Supplement 4).
To prove Theorem 2, we consider the more general problem of estimating sums of the form
for various integers and functions
, which we will take to be finitely supported to avoid issues of convergence.
Suppose that are supported on
; for simplicity, let us first assume the pointwise bound
for all
. (This simple case will not cover the case in Theorem 2, when
are truncated versions of the von Mangoldt function
, but will serve as a warmup to that case.) Then we have the trivial upper bound
A basic observation is that this upper bound is attainable if all “pretend” to behave like the same additive character
for some
. For instance, if
, then we have
when
, and then it is not difficult to show that
as .
The key to the success of the circle method lies in the converse of the above statement: the only way that the trivial upper bound (2) comes close to being sharp is when all correlate with the same character
, or in other words
are simultaneously large. This converse is largely captured by the following two identities:
Exercise 5 Let
be finitely supported functions. Then for any natural number
, show that
and
The traditional approach to using the circle method to compute sums such as proceeds by invoking (3) to express this sum as an integral over the unit circle, then dividing the unit circle into “major arcs” where
are large but computable with high precision, and “minor arcs” where one has estimates to ensure that
are small in both
and
senses. For functions
of number-theoretic significance, such as truncated von Mangoldt functions, the “major arcs” typically consist of those
that are close to a rational number
with
not too large, and the “minor arcs” consist of the remaining portions of the circle. One then obtains lower bounds on the contributions of the major arcs, and upper bounds on the contribution of the minor arcs, in order to get good lower bounds on
.
This traditional approach is covered in many places, such as this text of Vaughan. We will emphasise in this set of notes a slightly different perspective on the circle method, coming from recent developments in additive combinatorics; this approach does not quite give the sharpest quantitative estimates, but it allows for easier generalisation to more combinatorial contexts, for instance when replacing the primes by dense subsets of the primes, or replacing the equation with some other equation or system of equations.
From Exercise 5 and Hölder’s inequality, we immediately obtain
Corollary 6 Let
be finitely supported functions. Then for any natural number
, we have
Similarly for permutations of the
.
In the case when are supported on
and bounded by
, this corollary tells us that we have
is
whenever one has
uniformly in
, and similarly for permutations of
. From this and the triangle inequality, we obtain the following conclusion: if
is supported on
and bounded by
, and
is Fourier-approximated by another function
supported on
and bounded by
in the sense that
Thus, one possible strategy for estimating the sum is, one can effectively replace (or “model”)
by a simpler function
which Fourier-approximates
in the sense that the exponential sums
agree up to error
. For instance:
Exercise 7 Let
be a natural number, and let
be a random subset of
, chosen so that each
has an independent probability of
of lying in
.
- (i) If
and
, show that with probability
as
, one has
uniformly in
. (Hint: for any fixed
, this can be accomplished with quite a good probability (e.g.
) using a concentration of measure inequality, such as Hoeffding’s inequality. To obtain the uniformity in
, round
to the nearest multiple of (say)
and apply the union bound).
- (ii) Show that with probability
, one has
representations of the form
with
(with
treated as an ordered triple, rather than an unordered one).
In the case when is something like the truncated von Mangoldt function
, the quantity
is of size
rather than
. This costs us a logarithmic factor in the above analysis, however we can still conclude that we have the approximation (4) whenever
is another sequence with
such that one has the improved Fourier approximation
uniformly in . (Later on we will obtain a “log-free” version of this implication in which one does not need to gain a factor of
in the error term.)
This suggests a strategy for proving Vinogradov’s theorem: find an approximant to some suitable truncation
of the von Mangoldt function (e.g.
or
) which obeys the Fourier approximation property (5), and such that the expression
is easily computable. It turns out that there are a number of good options for such an approximant
. One of the quickest ways to obtain such an approximation (which is used in Chapter 19 of Iwaniec and Kowalski) is to start with the standard identity
, that is to say
and obtain an approximation by truncating to be less than some threshold
(which, in practice, would be a small power of
):
Thus, for instance, if , the approximant
would be taken to be
One could also use the slightly smoother approximation
in which case we would take
The function is somewhat similar to the continuous Selberg sieve weights studied in Notes 4, with the main difference being that we did not square the divisor sum as we will not need to take
to be non-negative. As long as
is not too large, one can use some sieve-like computations to compute expressions like
quite accurately. The approximation (5) can be justified by using a nice estimate of Davenport that exemplifies the Mobius pseudorandomness heuristic from Supplement 4:
Theorem 8 (Davenport’s estimate) For any
and
, we have
uniformly for all
. The implied constants are ineffective.
This estimate will be proven by splitting into two cases. In the “major arc” case when is close to a rational
with
small (of size
or so), this estimate will be a consequence of the Siegel-Walfisz theorem ( from Notes 2); it is the application of this theorem that is responsible for the ineffective constants. In the remaining “minor arc” case, one proceeds by using a combinatorial identity (such as Vaughan’s identity) to express the sum
in terms of bilinear sums of the form
, and use the Cauchy-Schwarz inequality and the minor arc nature of
to obtain a gain in this case. This will all be done below the fold. We will also use (a rigorous version of) the approximation (6) (or (7)) to establish Vinogradov’s theorem.
A somewhat different looking approximation for the von Mangoldt function that also turns out to be quite useful is
for some that is not too large compared to
. The methods used to establish Theorem 8 can also establish a Fourier approximation that makes (8) precise, and which can yield an alternate proof of Vinogradov’s theorem; this will be done below the fold.
The approximation (8) can be written in a way that makes it more similar to (7):
Exercise 9 Show that the right-hand side of (8) can be rewritten as
where
Then, show the inequalities
and conclude that
(Hint: for the latter estimate, use Theorem 27 of Notes 1.)
The coefficients in the above exercise are quite similar to optimised Selberg sieve coefficients (see Section 2 of Notes 4).
Another approximation to , related to the modified Cramér random model (see Model 10 of Supplement 4) is
where and
is a slowly growing function of
(e.g.
); a closely related approximation is
for as above and
coprime to
. These approximations (closely related to a device known as the “
-trick”) are not as quantitatively accurate as the previous approximations, but can still suffice to establish Vinogradov’s theorem, and also to count many other linear patterns in the primes or subsets of the primes (particularly if one injects some additional tools from additive combinatorics, and specifically the inverse conjecture for the Gowers uniformity norms); see this paper of Ben Green and myself for more discussion (and this more recent paper of Shao for an analysis of this approach in the context of Vinogradov-type theorems). The following exercise expresses the approximation (9) in a form similar to the previous approximation (8):
Exercise 10 With
as above, show that
for all natural numbers
.
— 1. Exponential sums over primes: the minor arc case —
We begin by developing some simple rigorous instances of the following general heuristic principle (cf. Section 3 of Supplement 4):
Principle 11 (Equidistribution principle) An exponential sum (such as a linear sum
or a bilinear sum
involving a “structured” phase function
should exhibit some non-trivial cancellation, unless there is an “obvious” algebraic reason why such cancellation may not occur (e.g.
is approximately periodic with small period, or
approximately decouples into a sum
).
There are some quite sophisticated versions of this principle in the literature, such as Ratner’s theorems on equidistribution of unipotent flows, discussed in this previous blog post. There are yet further precise instances of this principle which are conjectured to be true, but for which this remains unproven (e.g. regarding incomplete Weil sums in finite fields). Here, though, we will focus only on the simplest manifestations of this principle, in which is a linear or bilinear phase. Rigorous versions of this special case of the above principle will be very useful in estimating exponential sums such as
or
in “minor arc” situations in which is not too close to a rational number
of small denominator. The remaining “major arc” case when
is close to such a rational number
has to be handled by the complementary methods of multiplicative number theory, which we turn to later in this section.
For pedagogical reasons we shall develop versions of this principle that are in contrapositive form, starting with a hypothesis that a significant bias in an exponential sum is present, and deducing algebraic structure as a consequence. This leads to estimates that are not fully optimal from a quantitative viewpoint, but I believe they give a good qualitative illustration of the phenomena being exploited here.
We begin with the simplest instance of Principle 11, namely regarding unweighted linear sums of linear phases:
Lemma 12 Let
be an interval of length at most
for some
, let
, and let
.
- (i) If
Then
, where
denotes the distance from (any representative of)
to the nearest integer.
- (ii) More generally, if
for some monotone function
, then
.
Proof: From the geometric series formula we have
and the claim (i) follows. To prove (ii), we write and observe from summation by parts that
while from monotonicity we have
and the claim then follows from (i) and the pigeonhole principle.
Now we move to bilinear sums. We first need an elementary lemma:
Lemma 13 (Vinogradov lemma) Let
be an interval of length at most
for some
, and let
be such that
for at least
values of
, for some
. Then either
or
or else there is a natural number
such that
One can obtain somewhat sharper estimates here by using the classical theory of continued fractions and Bohr sets, as in this previous blog post, but we will not need these refinements here.
Proof: We may assume that and
, since we are done otherwise. Then there are at least two
with
, and by the pigeonhole principle we can find
in
with
and
. By the triangle inequality, we conclude that there exists at least one natural number
for which
We take to be minimal amongst all such natural numbers, then we see that there exists
coprime to
and
such that
If then we are done, so suppose that
. Suppose that
are elements of
such that
and
. Writing
for some
, we have
By hypothesis, ; note that as
and
we also have
. This implies that
and thus
. We then have
We conclude that for fixed with
, there are at most
elements
of
such that
. Iterating this with a greedy algorithm, we see that the number of
with
is at most
; since
, this implies that
and the claim follows.
Now we can control bilinear sums of the form
Theorem 14 (Bilinear sum estimate) Let
, let
be an interval, and let
,
be sequences supported on
and
respectively. Let
and
.
- (i) (Type I estimate) If
is real-valued and monotone and
then either
, or there exists
such that
.
- (ii) (Type II estimate) If
then either
, or there exists
such that
.
The hypotheses of (i) and (ii) should be compared with the trivial bounds
and
arising from the triangle inequality and the Cauchy-Schwarz inequality.
Proof: We begin with (i). By the triangle inequality, we have
The summand in is bounded by
. We conclude that
for at least choices of
(this is easiest to see by arguing by contradiction). Applying Lemma 12(ii), we conclude that
for at least choices of
. Applying Lemma 13, we conclude that one of
,
, or there exists a natural number
such that
. This gives (i) except when
. In this case, we return to (12), which holds for at least one natural number
, and set
.
Now we prove (ii). By the triangle inequality, we have
and hence by the Cauchy-Schwarz inequality
The left-hand side expands as
from the triangle inequality, the estimate and symmetry we conclude that
for at least one choice of . Fix this
. Since
, we thus have
for choices of
. Applying Lemma 12(i), we conclude that
for choices of
. Applying Lemma 13, we obtain the claim.
The following exercise demonstrates the sharpness of the above theorem, at least with regards to the bound on .
Exercise 15 Let
be a rational number with
, let
, and let
be multiples of
.
- (i) If
for a sufficiently small absolute constant
, show that
.
- (ii) If
is even, and
for a sufficiently small absolute constant
, show that
.
Exercise 16 (Quantitative Weyl exponential sum estimates) Let
be a polynomial with coefficients
for some
, let
, and let
.
- (i) Suppose that
for some interval
of length at most
. Show that there exists a natural number
such that
. (Hint: induct on
and use the van der Corput inequality (Proposition 7 of Notes 5).
- (ii) Suppose that
for some interval
contained in
. Show that there exists a natural number
such that
for all
(note this claim is trivial for
). (Hint: use downwards induction on
, adjusting
as one goes along, and split up
into somewhat short arithmetic progressions of various spacings
in order to turn the top degree components of
into essentially constant phases.)
- (iii) Use these bounds to give an alternate proof of Exercise 8 of Notes 5.
We remark that sharper versions of the above exercise are available if one uses the Vinogradov mean value theorem from Notes 5; see Theorem 1.6 of this paper of Wooley.
Exercise 17 (Quantitative multidimensional Weyl exponential sum estimates) Let
be a polynomial in
variables with coefficients
for some
. Let
and
. Suppose that
Show that either one has
for some
, or else there exists a natural number
such that
for all
. (Note: this is a rather tricky exercise, and is only recommended for students who have mastered the arguments needed to solve the one-dimensional version of this exercise from Exercise 16. A solution is given in this blog post.)
Recall that in the proof of the Bombieri-Vinogradov theorem (see Notes 3), sums such as or
were handled by using combinatorial identities such as Vaughan’s identity to split
or
into combinations of Type I or Type II convolutions. The same strategy can be applied here:
Proposition 18 (Minor arc exponential sums are small) Let
,
, and
, and let
be an interval in
. Suppose that either
Then either
, or there exists a natural number
such that
.
The exponent in the bound can be made explicit (and fairly small) if desired, but this exponent is not of critical importance in applications. The losses of
in this proposition are undesirable (though affordable, for the purposes of proving results such as Vinogradov’s theorem); these losses have been reduced over the years, and finally eliminated entirely in the recent work of Helfgott.
Proof: We will prove this under the hypothesis (13); the argument for (14) is similar and is left as an exercise. By removing the portion of in
, and shrinking
slightly, we may assume without loss of generality that
.
We recall the Vaughan identity
valid for any ; see Lemma 18 of Notes 3. We select
. By the triangle inequality, one of the assertions
must hold. If (15) holds, then , from which we easily conclude that
. Now suppose that (16) holds. By dyadic decomposition, we then have
where are restrictions of
,
to dyadic intervals
,
respectively. Note that the location of
then forces
, and the support of
forces
, so that
. Applying Theorem 14(i), we conclude that either
(and hence
), or else there is
such that
, and we are done.
Similarly, if (17) holds, we again apply dyadic decomposition to arrive at (19), where are now restrictions of
and
to
and
. As before, we have
, and now
and so
. Note from the identity
that
is bounded pointwise by
. Repeating the previous argument then gives one of the required conclusions.
Finally, we consider the “Type II” scenario in which (18) holds. We again dyadically decompose and arrive at (19), where and
are now the restrictions of
and
(say) to
and
, so that
,
, and
. As before we can bound
pointwise by
. Applying Theorem 14(ii), we conclude that either
, or else there exists
such that
, and we again obtain one of the desired conclusions.
Exercise 19 Finish the proof of Proposition 18 by treating the case when (14) occurs.
Exercise 20 Establish a version of Proposition 18 in which (13) or (14) are replaced with
— 2. Exponential sums over primes: the major arc case —
Proposition 18 provides guarantees that exponential sums such as are much smaller than
, unless
is itself small, or if
is close to a rational number
of small denominator. We now analyse this latter case. In contrast with the minor arc analysis, the implied constants will usually be ineffective.
The situation is simplest in the case of the Möbius function:
Proposition 21 Let
be an interval in
for some
, and let
. Then for any
and natural number
, we have
The implied constants are ineffective.
Proof: By splitting into residue classes modulo , it suffices to show that
for all . Writing
, and removing a factor of
, it suffices to show that
where is the representative of
that is closest to the origin, so that
.
For all in the above sum, one has
. From the fundamental theorem of calculus, one has
and so by the triangle inequality it suffices to show that
for all . But this follows from the Siegel-Walfisz theorem for the Möbius function (Exercise 66 of Notes 2).
Arguing as in the proof of Lemma 12(ii), we also obtain the corollary
for any monotone function , with ineffective constants.
Davenport’s theorem (Theorem 8) is now immediate from applying Proposition 18 with , followed by Proposition 21 (with
replaced by a larger constant) to deal with the major arc case.
Now we turn to the analogous situation for the von Mangoldt function . Here we expect to have a non-trivial main term in the major arc case: for instance, the prime number theorem tells us that
should be approximately the length of
when
. There are several ways to describe the behaviour of
. One way is to use the approximation
discussed in the introduction:
Proposition 22 Let
and let
be such that
. Then for any interval
in
and any
, one has
for all
. The implied constants are ineffective.
Proof: As discussed in the introduction, we have
so the left-hand side of (22) can be rearranged as
Since , the inner sum vanishes unless
. From Theorem 8 and summation by parts (or (21) and Proposition 21), we have
since , we have
, and the claim now follows from summing in
(and increasing
appropriately).
Exercise 23 Show that Proposition 22 continues to hold if
is replaced by the function
or more generally by
where
is a bounded function such that
for
and
for
. (Hint: use a suitable linear combination of the identities
and
.)
Alternatively, we can try to replicate the proof of Proposition 21 directly, keeping track of the main terms that are now present in the Siegel-Walfisz theorem. This gives a quite explicit approximation for in major arc cases:
Proposition 24 Let
be an interval in
for some
, and let
be of the form
, where
is a natural number,
, and
. Then for any
, we have
The implied constants are ineffective.
Proof: We may assume that and
, as the claim follows from the triangle inequality and the prime number theorem otherwise. For similar reasons we can also assume that
is sufficiently large depending on
.
As in the proof of Proposition 21, we decompose into residue classes mod to write
If is not coprime to
, then one easily verifies that
and the contribution of these cases is thus acceptable. Thus, up to negligible errors, we may restrict to be coprime to
. Writing
, we thus may replace
by
Applying (20), we can write
Applying the Siegel-Walfisz theorem (Exercise 64 of Notes 2), we can replace here by
, up to an acceptable error. Applying (20) again, we have now replaced
by
which we can rewrite as
From Möbius inversion one has
so we can rewrite the previous expression as
For with
, we see from the hypotheses that
, and so
by Lemma 12(i). The contribution of all
is then
, which is acceptable since
. So, up to acceptable errors, we may replace
by
. We can write
, and the claim now follows from Exercise 11 of Notes 1 and a change of variables.
Exercise 25 Assuming the generalised Riemann hypothesis, obtain the significantly stronger estimate
with effective constants. (Hint: use Exercise 48 of Notes 2, and adjust the arguments used to prove Proposition 24 accordingly.)
Exercise 26 If
and there is a real primitive Dirichlet character
of modulus
whose
-function
has an exceptional zero
with
for a sufficiently small
, establish the variant
of Proposition 24, with the implied constants now effective and with the Gauss sum
defined in equation (11) of Supplement 2. If there is no such primitive Dirichlet character, show that the above estimate continues to hold with the exceptional term
deleted.
Informally, the above exercise suggests that one should add an additional correction term to the model for
when there is an exceptional zero.
We can now formalise the approximation (8):
Exercise 27 Let
, and suppose that
is sufficiently large depending on
. Let
, and let
be a quantity with
. Let
be the function
Show that for any interval
, we have
for all
, with ineffective constants.
We also can formalise the approximations (9), (10):
Exercise 28 Let
, and let
be such that
. Write
.
- (i) Show that
for all
and
, with an ineffective constant.
- (ii) Suppose now that
and
. Let
be coprime to
, and let
. Show that
for all
and
.
Proposition 24 suggests that the exponential sum should be of size about
when
is close to
and
is fairly small, and
is large. However, the arguments in Proposition 18 only give an upper bound of
instead (ignoring logarithmic factors). There is a good reason for this discrepancy, though. The proof of Proposition 24 relied on the Siegel-Walfisz theorem, which in turn relied on Siegel’s theorem. As discussed in Notes 2, the bounds arising from this theorem are ineffective – we do not have any control on how the implied constant in the estimate in Proposition 24 depends on
. In contrast, the upper bounds in Proposition 18 are completely effective. Furthermore, these bounds are close to sharp in the hypothetical scenario of a Landau-Siegel zero:
Exercise 29 Let
be a sufficiently small (effective) absolute constant. Suppose there is a non-principal character
of conductor
with an exceptional zero
. Let
be such that
and
. Show that
for every
.
This exercise indicates that apart from the factors of , any substantial improvements to Proposition 18 will first require some progress on the notorious Landau-Siegel zero problem. It also indicates that if a Landau-Siegel zero is present, then one way to proceed is to simply incorporate the effect of that zero into the estimates (so that the computations for major arc exponential sums would acquire an additional main term coming from the exceptional zero), and try to establish results like Vinogradov’s theorem separately in this case (similar to how things were handled for Linnik’s theorem, see Notes 7), by using something like Exercise 26 in place of Proposition 24.
— 3. Vinogradov’s theorem —
We now have a number of routes to establishing Theorem 2. Let be a large number. We wish to compute the expression
or equivalently
where .
Now we replace by a more tractable approximation
. There are a number of choices for
that were presented in the previous section. For sake of illustration, let us select the choice
where (say) and where
is a fixed smooth function supported on
such that
for
. From Exercise 23 we have
(with ineffective constants) for any . Also, by bounding
by the divisor function on
we have the bounds
so from several applications of Corollary 6 (splitting as the sum of
and
) we have
for any (again with ineffective constants).
Now we compute . Using (23), we may rearrange this expression as
The inner sum can be estimated by covering the parameter space by squares of sidelength
(the least common multiple of
) as
where is the proportion of residue classes in the plane
with
. Since
, the contribution of the error term is certainly acceptable, so
Thus to prove Theorem 2, it suffices to establish the asymptotic
From the Chinese remainder theorem we see that is multiplicative in the sense that
when
is coprime to
, so to evaluate this quantity for squarefree
it suffices to do so when
for a single prime
. This is easily done:
except when
, in which case one has
The left-hand side of (24) is an expression similar to that studied in Section 2 of Notes 4, and can be estimated in a similar fashion. Namely, we can perform a Fourier expansion
for some smooth, rapidly decreasing . This lets us write the left-hand side of (24) as
where (by Exercise 30)
From Mertens’ theorem we see that
so from the rapid decrease of we may restrict
to be bounded in magnitude by
accepting a negligible error of
. Using
for , we can write
By Taylor expansion, we have
(say) uniformly for , and so the logarithm of the product
is a bounded holomorphic function in this region. From Taylor expansion we thus have
when , where
is some polynomial (depending on
) with vanishing constant term. From (1) we see that
Similarly we have
for , where
is another polynomial depending on
with vanishing constant term. We can thus write (26) (up to errors of
) as
where is a polynomial depending on
with vanishing constant term. By the rapid decrease of
we may then remove the constraints on
, and reduce (24) to showing that
which on expanding and Fubini’s theorem reduces to showing that
for . But from multiplying (25) by
and then differentiating
times at
, we see that
and the claim follows since for
. This proves Theorem 2 and hence Theorem 1.
One can of course use other approximations to to establish Vinogradov’s theorem. The following exercise gives one such route:
Exercise 31 Use Exercise 27 to obtain the asymptotic
for any
with ineffective constants. Then show that
and give an alternate derivation of Theorem 2.
Exercise 32 By using Exercise 26 in place of Exercise 27, obtain the asymptotic
for any
with effective constants if there is a real primitive Dirichlet character
of modulus
and modulus
and an exceptional
with
for some sufficiently small
and for some sufficiently large
depending on
, with the
term being deleted if no such exceptional character exists. Use this to establish Theorem 1 with an effective bound on how sufficiently large
has to be.
Exercise 33 Let
. Show that
for any
, where
Conclude that the number of length three arithmetic progressions
contained in the primes up to
is
for any
. (This result is due to van der Corput.)
Exercise 34 (Even Goldbach conjecture for most
) Let
, and let
be as in (23).
- (i) Show that
for any
and any function
bounded in magnitude by
.
- (ii) For any
, show that
for any
, where
- (iii) Show that for any
, one has
for all but at most
of the numbers
.
- (iv) Show that all but at most
of the even numbers in
are expressible as the sum of two primes.

25 comments
Comments feed for this article
30 March, 2015 at 2:58 pm
Anonymous
Partition function problem (about 20 lines before Thm 1) N and p(N)
[Corrected, thanks – T.]
30 March, 2015 at 10:32 pm
Anonymous
In exercise 7, it is not clear which probability is assigned to each
is assigned to each 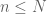 .
.
[Corrected, thanks – T.]
31 March, 2015 at 1:14 am
Anonymous
Let be a subset of the primes. What is the strongest known condition on the distribution of
be a subset of the primes. What is the strongest known condition on the distribution of  such that (at least probabilistically) its sumset
such that (at least probabilistically) its sumset  contains almost any even number.
contains almost any even number.
31 March, 2015 at 1:27 am
Anonymous
Of course, “strongest” above should be “weakest”.
31 March, 2015 at 5:37 am
Terence Tao
I’m not sure what you mean by “probabilistically” here, but it is possible to find sets S of primes of relative density arbitrarily close to 1 for which S+S does not contain almost every even number. For instance, if W is the product of all the primes less than or equal to w, let S be the set of primes p larger than w such that . Then S+S avoids the residue class
. Then S+S avoids the residue class  but has density
but has density  , which goes to one as w goes to infinity.
, which goes to one as w goes to infinity.
31 March, 2015 at 9:46 pm
Anonymous
“probabilistically” was meant to be “under appropriate probabilistic model”. In your example It is clear that avoids the residue class
avoids the residue class  but it is still not sufficiently clear how the last expression for the density of
but it is still not sufficiently clear how the last expression for the density of  was derived.
was derived.
1 April, 2015 at 9:11 am
Terence Tao
The complement of S consists of the primes lying in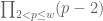 primitive residue classes modulo W, and the density claim then follows from the prime number theorem in arithmetic progressions.
primitive residue classes modulo W, and the density claim then follows from the prime number theorem in arithmetic progressions.
1 April, 2015 at 11:11 pm
Anonymous
Thanks for the explanation! (I misunderstood your previous explanation “but has density …” as referring to the density of – instead of the relative density of
– instead of the relative density of  ).
). is the set of twin primes, is it still possible (according to the current knowledge) that
is the set of twin primes, is it still possible (according to the current knowledge) that  contains almost every even positive integer?
contains almost every even positive integer?
In the case where
2 April, 2015 at 1:44 pm
Terence Tao
The set of twin primes (primes
of twin primes (primes  such that
such that 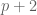 is also prime) consists almost entirely of primes that are
is also prime) consists almost entirely of primes that are  , so
, so  consists almost entirely of even numbers that are
consists almost entirely of even numbers that are 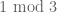 . Cramer model or Hardy-Littlewood prime tuple models predict though that this is basically the only obstruction, indeed
. Cramer model or Hardy-Littlewood prime tuple models predict though that this is basically the only obstruction, indeed  should contain all but finitely many numbers that are
should contain all but finitely many numbers that are 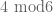 .
.
31 March, 2015 at 3:03 am
murugan ramar
i have new analysis operators and functional spaces
31 March, 2015 at 6:16 am
arch1
As a beginner I’m a puzzled by 7(ii). If the independent probability were 1 instead of ½, and order didn’t matter, wouldn’t the coefficient be 1/12? So why isn’t the coefficient in the problem either 1/(8*12) (if order doesn’t matter) or 6/(8*12) (if it does)?
[Corrected, thanks – T.]
1 April, 2015 at 6:48 am
gninrepoli
Interesting post. An alternative formula for the function Mangoldt:
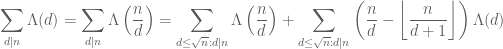

Using the Mobius inversion:
3 April, 2015 at 10:22 am
conic3bundle1surfaces4
“see ??? below” should perhaps be “see Exercise 34 below” ?
[Corrected, thanks – T.]
4 April, 2015 at 9:41 am
edwinjose
Out of topic question: Are there people studying numbers with 3 or more factors? What is the status of the twin 3-factor number conjecture? Perhaps the twin 2-factor number conjecture is just a special case of twin n-factor numbers. I want to know what is the latest in n-factor number research.
26 April, 2015 at 1:14 am
Anonymous
Can you clarify what the symbol $\||$ means?
26 April, 2015 at 10:50 am
Vinogradov’s theorem, Part 1 | Intelligible Mathematics
[…] am trying to read the blog post by Terence Tao on the Hardy-Littlewood circle method and Vinogradov’s […]
1 June, 2015 at 10:03 am
Asier Calbet Rípodas
I was reading your initial comments on the distinction between multiplicative and additive number theory, which are almost always kept separate. However, it occurs to me that studying the Dirichlet Divisor Problem, for example, can be seen as a problem in both additive and multiplicative number theory – indeed, the divisor function can be recovered from the square of the riemann zeta function, but the generating function of the divisor function can also be used via the circle method. Any further thoughts on this? Is the divisor function “special” in this sense, or are there other “overlaps” between additive number theory via the circle method and multiplicative number theory via the riemann zeta function?
1 June, 2015 at 10:41 am
Terence Tao
A few problems are lucky enough to have both exploitable additive and multiplicative structure (the counting of primes in arithmetic progressions is another example). I don’t view the two methods as being completely exclusive, and sometimes one needs a combination of the two methods (as well as possibly some other inputs as well) to solve a given analytic number theory problem. And of course there are no shortage of problems for which there is neither exploitable additive structure or exploitable multiplicative structure…
6 August, 2015 at 10:55 am
Equidistribution for multidimensional polynomial phases | What's new
[…] second lemma (which we recycle from this previous blog post) is a variant of the equidistribution […]
2 December, 2015 at 1:51 pm
A conjectural local Fourier-uniformity of the Liouville function | What's new
[…] Since is significantly larger than , standard Vinogradov-type manipulations (see e.g. Lemma 13 of these previous notes) show that this bad case occurs for many only when is “major arc”, which is the case […]
30 August, 2016 at 4:09 pm
Heuristic computation of correlations of the divisor function | What's new
[…] at the current level of technology, is to apply the Hardy-Littlewood circle method (discussed in this previous post) to express (2) in terms of exponential sums for various frequencies . The contribution of […]
4 September, 2019 at 1:47 pm
254A announcement: Analytic prime number theory | What's new
[…] The circle method […]
17 December, 2019 at 8:27 am
254A, Notes 10 – mean values of nonpretentious multiplicative functions | What's new
[…] into major and minor arcs in the circle method applied to additive number theory problems; see Notes 8. The Möbius and Liouville functions are model examples of non-pretentious functions; see […]
23 May, 2022 at 8:04 pm
Quân Nguyễn
Dear prof Tao,
“As in Proposition 24” should have been 21?
[Corrected, thanks – T.]
Also, in exercise 31, set and use Exercise 9 and properties of
and use Exercise 9 and properties of 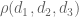 , I obtain:
, I obtain:
where the second sum over not all equal and which seems closely related but hopeless to get to the final sum:
not all equal and which seems closely related but hopeless to get to the final sum:
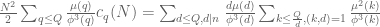
Any hint would be highly appreciated. Thank you for your time.
[Don’t try to use Exercise 9; instead evaluate the exponential sums directly via familiar Fourier-analytic manipulations. -T.]
4 September, 2022 at 10:16 am
Quân Nguyễn
Dear prof Tao,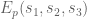 as in section 3? How can one know which terms are there in
as in section 3? How can one know which terms are there in  ? Thank you for your time.
? Thank you for your time.
Maybe this is not a good question but how can one factor the product into
[Any (absolutely convergent) sum of a multiplicative function in one or more variables can be factored into an Euler product. For instance for multiplicative
for multiplicative  , and similarly for sums in multiple varables. -T]
, and similarly for sums in multiple varables. -T]