One theme in this course will be the central nature played by the gaussian random variables . Gaussians have an incredibly rich algebraic structure, and many results about general random variables can be established by first using this structure to verify the result for gaussians, and then using universality techniques (such as the Lindeberg exchange strategy) to extend the results to more general variables.
One way to exploit this algebraic structure is to continuously deform the variance from an initial variance of zero (so that the random variable is deterministic) to some final level
. We would like to use this to give a continuous family
of random variables
as
(viewed as a “time” parameter) runs from
to
.
At present, we have not completely specified what should be, because we have only described the individual distribution
of each
, and not the joint distribution. However, there is a very natural way to specify a joint distribution of this type, known as Brownian motion. In these notes we lay the necessary probability theory foundations to set up this motion, and indicate its connection with the heat equation, the central limit theorem, and the Ornstein-Uhlenbeck process. This is the beginning of stochastic calculus, which we will not develop fully here.
We will begin with one-dimensional Brownian motion, but it is a simple matter to extend the process to higher dimensions. In particular, we can define Brownian motion on vector spaces of matrices, such as the space of Hermitian matrices. This process is equivariant with respect to conjugation by unitary matrices, and so we can quotient out by this conjugation and obtain a new process on the quotient space, or in other words on the spectrum of
Hermitian matrices. This process is called Dyson Brownian motion, and turns out to have a simple description in terms of ordinary Brownian motion; it will play a key role in several of the subsequent notes in this course.
— 1. Formal construction of Brownian motion —
We begin with constructing one-dimensional Brownian motion. We shall model this motion using the machinery of Wiener processes:
Definition 1 (Wiener process) Let
, and let
be a set of times containing
. A (one-dimensional) Wiener process on
with initial position
is a collection
of real random variables
for each time
, with the following properties:
- (i)
.
- (ii) Almost surely, the map
is a continuous function on
.
- (iii) For every
in
, the increment
has the distribution of
. (In particular,
for every
.)
- (iv) For every
in
, the increments
for
are jointly independent.
If
is discrete, we say that
is a discrete Wiener process; if
then we say that
is a continuous Wiener process.
Remark 2 Collections of random variables
, where
is a set of times, will be referred to as stochastic processes, thus Wiener processes are a (very) special type of stochastic process.
Remark 3 In the case of discrete Wiener processes, the continuity requirement (ii) is automatic. For continuous Wiener processes, there is a minor technical issue: the event that
is continuous need not be a measurable event (one has to take uncountable intersections to define this event). Because of this, we interpret (ii) by saying that there exists a measurable event of probability
, such that
is continuous on all of this event, while also allowing for the possibility that
could also sometimes be continuous outside of this event also. One can view the collection
as a single random variable, taking values in the product space
(with the product
-algebra, of course).
Remark 4 One can clearly normalise the initial position
of a Wiener process to be zero by replacing
with
for each
.
We shall abuse notation somewhat and identify continuous Wiener processes with Brownian motion in our informal discussion, although technically the former is merely a model for the latter. To emphasise this link with Brownian motion, we shall often denote continuous Wiener processes as rather than
.
It is not yet obvious that Wiener processes exist, and to what extent they are unique. The situation is easily clarified though for discrete processes:
Proposition 5 (Discrete Brownian motion) Let
be a discrete subset of
containing
, and let
. Then (after extending the sample space if necessary) there exists a Wiener process
with base point
. Furthermore, any other Wiener process
with base point
has the same distribution as
.
Proof: As is discrete and contains
, we can write it as
for some
Let be a collection of jointly independent random variables with
(the existence of such a collection, after extending the sample space, is guaranteed by Exercise 18 of Notes 0.) If we then set
for all , then one easily verifies (using Exercise 9 of Notes 1) that
is a Wiener process.
Conversely, if is a Wiener process, and we define
for
, then from the definition of a Wiener process we see that the
have distribution
and are jointly independent (i.e. any finite subcollection of the
are jointly independent). This implies for any finite
that the random variables
and
have the same distribution, and thus
and
have the same distribution for any finite subset
of
. From the construction of the product
-algebra we conclude that
and
have the same distribution, as required.
Now we pass from the discrete case to the continuous case.
Proposition 6 (Continuous Brownian motion) Let
. Then (after extending the sample space if necessary) there exists a Wiener process
with base point
. Furthermore, any other Wiener process
with base point
has the same distribution as
.
Proof: The uniqueness claim follows by the same argument used to prove the uniqueness component of Proposition 5, so we just prove existence here. The iterative construction we give here is somewhat analogous to that used to create self-similar fractals, such as the Koch snowflake. (Indeed, Brownian motion can be viewed as a probabilistic analogue of a self-similar fractal.)
The idea is to create a sequence of increasingly fine discrete Brownian motions, and then to take a limit. Proposition 5 allows one to create each individual discrete Brownian motion, but the key is to couple these discrete processes together in a consistent manner.
Here’s how. We start with a discrete Wiener process on the natural numbers
with initial position
, which exists by Proposition 5. We now extend this process to the denser set of times
by setting
for , where
are iid copies of
, which are jointly independent of the
. It is a routine matter to use Exercise 9 of Notes 1 to show that this creates a discrete Wiener process
on
which extends the previous process.
Next, we extend the process further to the denser set of times by defining
where are iid copies of
, jointly independent of
. Again, it is a routine matter to show that this creates a discrete Wiener process
on
.
Iterating this procedure a countable number of times, we obtain a collection of discrete Wiener processes for
which are consistent with each other, in the sense that the earlier processes in this collection are restrictions of later ones. (This requires a countable number of extensions of the underlying sample space, but one can capture all of these extensions into a single extension via the machinery of inverse limits of probability spaces; it is also not difficult to manually build a single extension sufficient for performing all the above constructions.)
Now we establish a Hölder continuity property. Let be any exponent between
and
, and let
be finite. Observe that for any
and any
, we have
and hence (by the subgaussian nature of the normal distribution)
for some absolute constants . The right-hand side is summable as
run over
subject to the constraint
. Thus, by the Borel-Cantelli lemma, for each fixed
, we almost surely have that
for all but finitely many with
. In particular, this implies that for each fixed
, the function
is almost surely Hölder continuous of exponent
on the dyadic rationals
in
, and thus (by the countable union bound) is almost surely locally Hölder continuous of exponent
on the dyadic rationals in
. In particular, they are almost surely locally uniformly continuous on this domain.
As the dyadic rationals are dense in , we can thus almost surely extend
uniquely to a continuous function on all of
. (On the remaining probability zero event, we extend
in some arbitrary measurable fashion.) Note that if
is any sequence in
converging to
, then
converges almost surely to
, and thus also converges in probability and in distribution. Similarly for differences such as
. Using this, we easily verify that
is a continuous Wiener process, as required.
Remark 7 One could also have used the Kolmogorov extension theorem to establish the limit.
Exercise 8 Let
be a continuous Wiener process. We have already seen that if
, that the map
is almost surely Hölder continuous of order
. Show that if
, then the map
is almost surely not Hölder continuous of order
.
Show also that the map
is almost surely nowhere differentiable. Thus, Brownian motion provides a (probabilistic) example of a continuous function which is nowhere differentiable.
Remark 9 In the above constructions, the initial position
of the Wiener process was deterministic. However, one can easily construct Wiener processes in which the initial position
is itself a random variable. Indeed, one can simply set
where
is a continuous Wiener process with initial position
which is independent of
. Then we see that
obeys properties (ii), (iii), (iv) of Definition 1, but the distribution of
is no longer
, but is instead the convolution of the law of
, and the law of
.
— 2. Connection with random walks —
We saw how to construct Brownian motion as a limit of discrete Wiener processes, which were partial sums of independent gaussian random variables. The central limit theorem (see Notes 2) allows one to interpret Brownian motion in terms of limits of partial sums of more general independent random variables, otherwise known as (independent) random walks.
Definition 10 (Random walk) Let
be a real random variable, let
be an initial position, and let
be a time step. We define a discrete random walk with initial position
, time step
and step distribution
(or
) to be a process
defined by
where
are iid copies of
.
Example 11 From the proof of Proposition 5, we see that a discrete Wiener process on
with initial position
is nothing more than a discrete random walk with step distribution of
. Another basic example is simple random walk, in which
is equal to
times a signed Bernoulli variable, thus we have
, where the signs
are unbiased and are jointly independent in
.
Exercise 12 (Central limit theorem) Let
be a real random variable with mean zero and variance
, and let
. For each
, let
be a process formed by starting with a random walk
with initial position
, time step
, and step distribution
, and then extending to other times in
, in a piecewise linear fashion, thus
for all
and
. Show that as
, the process
converges in distribution to a continuous Wiener process with initial position
. (Hint: from the Riesz representation theorem (or the Kolmogorov extension theorem), it suffices to establish this convergence for every finite set of times in
. Now use the central limit theorem; treating the piecewise linear modifications to the process as an error term.)
— 3. Connection with the heat equation —
Let be a Wiener process with base point
, and let
be a smooth function with all derivatives bounded. Then, for each time
, the random variable
is bounded and thus has an expectation
. From the almost sure continuity of
and the dominated convergence theorem we see that the map
is continuous. In fact it is differentiable, and obeys the following differential equation:
Lemma 13 (Equation of motion) For all times
, we have
where
is the second derivative of
. In particular,
is continuously differentiable (because the right-hand side is continuous).
Proof: We work from first principles. It suffices to show for fixed , that
as . We shall establish this just for non-negative
; the claim for negative
(which only needs to be considered for
) is similar and is left as an exercise.
Write . From Taylor expansion and the bounded third derivative of
, we have
We take expectations. Since , we have
, so in particular
Now observe that is independent of
, and has mean zero and variance
. The claim follows.
Exercise 14 Complete the proof of the lemma by considering negative values of
. (Hint: one has to exercise caution because
is not independent of
in this case. However, it will be independent of
. Also, use the fact that
and
are continuous in
. Alternatively, one can deduce the formula for the left-derivative from that of the right-derivative via a careful application of the fundamental theorem of calculus, paying close attention to the hypotheses of that theorem.)
Remark 15 In the language of Ito calculus, we can write (1) as
Here,
, and
should either be thought of as being infinitesimal, or being very small, though in the latter case the equation (2) should not be viewed as being exact, but instead only being true up to errors of mean
and third moment
. This is a special case of Ito’s formula. It should be compared against the chain rule
when
is a smooth process. The non-smooth nature of Brownian motion causes the quadratic term in the Taylor expansion to be non-negligible, which explains the additional term in (2), although the Hölder continuity of this motion is sufficient to still be able to ignore terms that are of cubic order or higher. (In this spirit, one can summarise (the differential side of) Ito calculus informally by the heuristic equations
and
, with the understanding that all terms that are
are discarded.)
Let be the probability density function of
; by inspection of the normal distribution, this is a smooth function for
, but is a Dirac mass at
at time
. By definition of density function,
for any Schwartz function . Applying Lemma 13 and integrating by parts, we see that
in the sense of (tempered) distributions (see e.g. my earlier notes on this topic). In other words, is a (tempered distributional) solution to the heat equation (3). Indeed, since
is the Dirac mass at
at time
,
for later times
is the fundamental solution of that equation from initial position
.
From the theory of PDE (e.g. from Fourier analysis, see Exercise 38 of these notes) one can solve the (distributional) heat equation with this initial data to obtain the unique solution
Of course, this is also the density function of , which is (unsurprisingly) consistent with the fact that
. Thus we see why the normal distribution of the central limit theorem involves the same type of functions (i.e. gaussians) as the fundamental solution of the heat equation. Indeed, one can use this argument to heuristically derive the central limit theorem from the fundamental solution of the heat equation (cf. Section 7 of Notes 2), although the derivation is only heuristic because one first needs to know that some limiting distribution already exists (in the spirit of Exercise 12).
Remark 16 Because we considered a Wiener process with a deterministic initial position
, the density function
was a Dirac mass at time
. However, one can run exactly the same arguments for Wiener processes with stochastic initial position (see Remark 9), and one will still obtain the same heat equation (9), but now with a more general initial condition.
We have related one-dimensional Brownian motion to the one-dimensional heat equation, but there is no difficulty establishing a similar relationship in higher dimensions. In a vector space , define a (continuous) Wiener process
in
with an initial position
to be a process whose components
for
are independent Wiener processes with initial position
. It is easy to see that such processes exist, are unique in distribution, and obey the same sort of properties as in Definition 1, but with the one-dimensional gaussian distribution
replaced by the
-dimensional analogue
, which is given by the density function
where is now Lebesgue measure on
.
Exercise 17 If
is an
-dimensional continuous Wiener process, show that
whenever
is smooth with all derivatives bounded, where
is the Laplacian of
. Conclude in particular that the density function
of
obeys the (distributional) heat equation
A simple but fundamental observation is that -dimensional Brownian motion is rotation-invariant: more precisely, if
is an
-dimensional Wiener process with initial position
, and
is any orthogonal transformation on
, then
is another Wiener process with initial position
, and thus has the same distribution:
This is ultimately because the -dimensional normal distributions
are manifestly rotation-invariant (see Exercise 10 of Notes 1).
Remark 18 One can also relate variable-coefficient heat equations to variable-coefficient Brownian motion
, in which the variance of an increment
is now only proportional to
for infinitesimal
rather than being equal to
, with the constant of proportionality allowed to depend on the time
and on the position
. One can also add drift terms by allowing the increment
to have a non-zero mean (which is also proportional to
). This can be accomplished through the machinery of stochastic calculus, which we will not discuss in detail in these notes. In a similar fashion, one can construct Brownian motion (and heat equations) on manifolds or on domains with boundary, though we will not discuss this topic here.
Exercise 19 Let
be a real random variable of mean zero and variance
. Define a stochastic process
by the formula
where
is a Wiener process with initial position zero that is independent of
. This process is known as an Ornstein-Uhlenbeck process.
- Show that each
has mean zero and variance
.
- Show that
converges in distribution to
as
.
- If
is smooth with all derivatives bounded, show that
where
is the Ornstein-Uhlenbeck operator
Conclude that the density function
of
obeys (in a distributional sense, at least) the Ornstein-Uhlenbeck equation
where the adjoint operator
is given by
- Show that the only probability density function
for which
is the Gaussian
; furthermore, show that
for all probability density functions
in the Schwartz space with mean zero and variance
. Discuss how this fact relates to the preceding two parts of this exercise.
Remark 20 The heat kernel
in
dimensions is absolutely integrable in time away from the initial time
for dimensions
, but becomes divergent in dimension
and (just barely) divergent for
. This causes the qualitative behaviour of Brownian motion
in
to be rather different in the two regimes. For instance, in dimensions
Brownian motion is transient; almost surely one has
as
. But in dimension
Brownian motion is recurrent: for each
, one almost surely has
for infinitely many
. In the critical dimension
, Brownian motion turns out to not be recurrent, but is instead neighbourhood recurrent: almost surely,
revisits every neighbourhood of
at arbitrarily large times, but does not visit
itself for any positive time
. The study of Brownian motion and its relatives is in fact a huge and active area of study in modern probability theory, but will not be discussed in this course.
— 4. Dyson Brownian motion —
The space of
Hermitian matrices can be viewed as a real vector space of dimension
using the Frobenius norm
where are the coefficients of
. One can then identify
explicitly with
via the identification
Now that one has this indentification, for each Hermitian matrix (deterministic or stochastic) we can define a Wiener process
on
with initial position
. By construction, we see that
is almost surely continuous, and each increment
is equal to
times a matrix drawn from the gaussian unitary ensemble (GUE), with disjoint increments being jointly independent. In particular, the diagonal entries of
have distribution
, and the off-diagonal entries have distribution
.
Given any Hermitian matrix , one can form the spectrum
, which lies in the Weyl chamber
. Taking the spectrum of the Wiener process
, we obtain a process
in the Weyl cone. We abbreviate as
.
For , we see that
is absolutely continuously distributed in
. In particular, since almost every Hermitian matrix has simple spectrum, we see that
has almost surely simple spectrum for
. (The same is true for
if we assume that
also has an absolutely continuous distribution.)
The stochastic dynamics of this evolution can be described by Dyson Brownian motion:
Theorem 21 (Dyson Brownian motion) Let
, and let
, and let
be as above. Then we have
for all
, where
, and
are iid copies of
which are jointly independent of
, and the error term
is the sum of two terms, one of which has
norm
, and the other has mean zero and second moment
in the limit
(holding
and
fixed).
Using the language of Ito calculus, one usually views as infinitesimal and drops the
error, thus giving the elegant formula
that shows that the eigenvalues evolve by Brownian motion, combined with a deterministic repulsion force that repels nearby eigenvalues from each other with a strength inversely proportional to the separation. One can extend the theorem to the
case by a limiting argument provided that
has an absolutely continuous distribution. Note that the decay rate of the error
can depend on
, so it is not safe to let
go off to infinity while holding
fixed. However, it is safe to let
go to zero first, and then send
off to infinity. (It is also possible, by being more explicit with the error terms, to work with
being a specific negative power of
. We will see this sort of analysis later in this course.)
Proof: Fix . We can write
, where
is independent of
and has the GUE distribution. (Strictly speaking,
depends on
, but this dependence will not concern us.) We now condition
to be fixed, and establish (5) for almost every fixed choice of
; the general claim then follows upon undoing the conditioning (and applying the dominated convergence theorem). Due to independence, observe that
continues to have the GUE distribution even after conditioning
to be fixed.
Almost surely, has simple spectrum; so we may assume that the fixed choice of
has simple spectrum also. Actually, we can say more: since the Wiener random matrix
has a smooth distribution in the space
of Hermitian matrices, while the space
of matrices in
with non-simple spectrum has codimension
by Exercise 10 of Notes 3a, we see that for any
the probability that
lies within
of
is
, where we allow implied constants to depend on
. In particular, if we let
denote the minimal eigenvalue gap, we have
which by dyadic decomposition implies the finite negative second moment
Let denote the derivative of the eigenvalue
in the
direction. From the first and second Hadamard variation formulae (see Section 4 of Notes 3a) we have
and
where are an orthonormal eigenbasis for
, and also
. A further differentiation then yields
(One can obtain a more exact third Hadamard variation formula if desired, but it is messy and will not be needed here.) A Taylor expansion now gives the bound
provided that one is in the regime
(in order to keep the eigenvalue gap at least as one travels from
to
). In the opposite regime
we can instead use the Weyl inequalities to bound ; the other two terms
in the Taylor expansion are also
in this case. Thus (7) holds in all cases.
Now we take advantage of the unitary invariance of the Gaussian unitary ensemble (that is, that for all unitary matrices
; this is easiest to see by noting that the probability density function of
is proportional to
). From this invariance, we can assume without loss of generality that
is the standard orthonormal basis of
, so that we now have
where are the coefficients of
. But the
are iid copies of
, so we will be done as soon as we show that the terms
are acceptable error terms. But the first term has mean zero and is bounded by and thus has second moment
by (6), while the second term has
norm of
, again by (6).
Remark 22 Interestingly, one can interpret Dyson Brownian motion in a different way, namely as the motion of
independent Wiener processes
after one conditions the
to be non-intersecting for all time; see this paper of Grabiner. It is intuitively reasonable that this conditioning would cause a repulsion effect, though I do not know of a simple heuristic reason why this conditioning should end up giving the specific repulsion force present in (5).
In the previous section, we saw how a Wiener process led to a PDE (the heat flow equation) that could be used to derive the probability density function for each component of that process. We can do the same thing here:
Exercise 23 Let
be as above. Let
be a smooth function with bounded derivatives. Show that for any
, one has
where
is the adjoint Dyson operator
If we let
denote the density function
of
at time
, deduce the Dyson partial differential equation
(in the sense of distributions, at least, and on the interior of
), where
is the Dyson operator
The Dyson partial differential equation (8) looks a bit complicated, but it can be simplified (formally, at least) by introducing the Vandermonde determinant
Exercise 24 Show that (10) is the determinant of the matrix
, and is also the sum
.
Note that this determinant is non-zero on the interior of the Weyl chamber . The significance of this determinant for us lies in the identity
which can be used to cancel off the second term in (9). Indeed, we have
Exercise 25 Let
be a smooth solution to (8) in the interior of
, and write
in this interior. Show that
obeys the linear heat equation
in the interior of
. (Hint: You may need to exploit the identity
for distinct
. Equivalently, you may need to first establish that the Vandermonde determinant is a harmonic function.)
Let be the density function of the
, as in (23). As previously remarked, the Wiener random matrix
has a smooth distribution in the space
of Hermitian matrices, while the space of matrices in
with non-simple spectrum has codimension
by Exercise 10 of Notes 3a. On the other hand, the non-simple spectrum only has codimension
in the Weyl chamber (being the boundary of this cone). Because of this, we see that
vanishes to at least second order on the boundary of this cone (with correspondingly higher vanishing on higher codimension facets of this boundary). Thus, the function
in Exercise 25 vanishes to first order on this boundary (again with correspondingly higher vanishing on higher codimension facets). Thus, if we extend
symmetrically across the cone to all of
, and extend the function
antisymmetrically, then the equation (8) and the factorisation (12) extend (in the distributional sense) to all of
. Extending (25) to this domain (and being somewhat careful with various issues involving distributions), we now see that
obeys the linear heat equation on all of
.
Now suppose that the initial matrix had a deterministic spectrum
, which to avoid technicalities we will assume to be in the interior of the Weyl chamber (the boundary case then being obtainable by a limiting argument). Then
is initially the Dirac delta function at
, extended symmetrically. Hence,
is initially
times the Dirac delta function at
, extended antisymmetrically:
Using the fundamental solution for the heat equation in dimensions, we conclude that
By the Leibniz formula for determinants, we can express the sum here as a determinant of the matrix
Applying (12), we conclude
Theorem 26 (Johansson formula) Let
be a Hermitian matrix with simple spectrum
, let
, and let
where
is drawn from GUE. Then the spectrum
of
has probability density function
on
.
This formula is given explicitly in this paper of Johansson, who cites this paper of Brézin and Hikami as inspiration. This formula can also be proven by a variety of other means, for instance via the Harish-Chandra formula. (One can also check by hand that (13) satisfies the Dyson equation (8).)
We will be particularly interested in the case when and
, so that we are studying the probability density function of the eigenvalues
of a GUE matrix
. The Johansson formula does not directly apply here, because
is vanishing. However, we can investigate the limit of (13) in the limit as
inside the Weyl chamber; the Lipschitz nature of the eigenvalue operations
(from the Weyl inequalities) tell us that if (13) converges locally uniformly as
for
in the interior of
, then the limit will indeed be the probability density function for
. (Note from continuity that the density function cannot assign any mass to the boundary of the Weyl chamber, and in fact must vanish to at least second order by the previous discussion.)
Exercise 27 Show that as
, we have the identities
and
locally uniformly in
. (Hint: for the second identity, use Taylor expansion and the Leibniz formula for determinants, noting the left-hand side vanishes whenever
vanishes and so can be treated by the (smooth) factor theorem.)
From the above exercise, we conclude the fundamental Ginibre formula
for the density function for the spectrum of a GUE matrix
.
This formula can be derived by a variety of other means; we sketch one such way below.
Exercise 28 For this exercise, assume that it is known that (14) is indeed a probability distribution on the Weyl chamber
(if not, one would have to replace the constant
by an unspecified normalisation factor depending only on
). Let
be drawn at random using the distribution (14), and let
be drawn at random from Haar measure on
. Show that the probability density function of
at a matrix
with simple spectrum is equal to
for some constant
. (Hint: use unitary invariance to reduce to the case when
is diagonal. Now take a small
and consider what
and
must be in order for
to lie within
of
in the Frobenius norm, performing first order calculations only (i.e. linearising and ignoring all terms of order
).)
Conclude that (14) must be the probability density function of the spectrum of a GUE matrix.
Exercise 29 Verify by hand that the self-similar extension
of the function (14) obeys the Dyson PDE (8). Why is this consistent with (14) being the density function for the spectrum of GUE?
Remark 30 Similar explicit formulae exist for other invariant ensembles, such as the gaussian orthogonal ensemble GOE and the gaussian symplectic ensemble GSE. One can also replace the exponent in density functions such as
with more general expressions than quadratic expressions of
. We will however not detail these formulae in this course (with the exception of the spectral distribution law for random iid gaussian matrices, which we will discuss in a later set of notes).

55 comments
Comments feed for this article
18 January, 2010 at 7:02 pm
Joshua Batson
I think last display in the proof of prop. 3 should be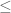 not
not 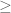 .
.
[Corrected, thanks – T.]
18 January, 2010 at 7:36 pm
Anonymous
Wonderful post. Everything looks different in your hands.
Thank you Prof. Tao.
19 January, 2010 at 8:32 am
Tim vB
Dear Terry,
marvelous lecture notes, thanks for making them public!
On a side note I would like to mention that it can be fun to code a discretization scheme for stochastic differential equations aka a simulation of a stochastic process, in order to solve the associated partial differential equation. It’s one thing to prove that it can be done, but it can be fun too to look at some specific examples and compare the results of the simulation with numerical or analytical results that you get from the partial differential equation.
That’s off topic with regard to your class of course, but maybe some of your students would like to takle that in their spare time, if they have any :-)
(I think that is still an active research topic, used e.g. for PDE with complicated domains/boundaries and boundary conditions, but I’ve been out of the field for years).
BTW: Do you use computer simulations in the class?
19 January, 2010 at 4:13 pm
David Speyer
Possible typo: In the paragraph beginning “Now we establish a Hölder continuity property. Let theta be any exponent between 0 and 2”, I think that 2 should be 1/2.
These are great notes; I am starting to understand what a random walk is.
19 January, 2010 at 5:43 pm
Anonymous
There are eleven “Formula does not parse” errors. I’m using Firefox 3.5.7. The first one is in the def of Wiener Process:
A (one-dimensional) Wiener process on {\Sigma} with initial position {\mu} is a collection {(X_t)_{t \in \Sigma}} of real random …
Here, {(X_t)_{t \in \Sigma}} does not parse.
19 January, 2010 at 7:22 pm
Jonathan Vos Post
I also get eleven “Formula does not parse” errors, using Firefox 3.5.7.
20 January, 2010 at 5:53 am
Tim vB
That does not seem to be a problem of the browser, I’m using Firefox 3.5.7 as well and all formulas are rendered without any problems, but I see them as embedded png graphics.
20 January, 2010 at 12:09 pm
Américo Tavares
A few hours ago I also got the same errors but now all formulas are OK. (I’m using IE).
25 January, 2010 at 7:45 pm
solrize
This post and and the post of a few days ago reviewing probability theory are great. It’s important material that I’ve been wanting to understand for quite a while. I’ve looked at some elementary books that were muddled and left out all the interesting stuff, and I’ve looked at some more advanced books that had way too much assumed background for me (ex-undergrad math major) to understand. These posts of yours are at a level that I think I can make my way through if I work at it, and which appear to demystify the subject. That’s hard to find. Thanks!!!!
28 January, 2010 at 11:30 am
Doug
Hi Terrence,
I have found a discussion of the LOUIS BACHELIER 1900 thesis “THEORIE DE LA SPECULATION” with Brownian motion applied to the stock market [Mathematical Finance, Vol.10, No.3 (July 2000), 341–353].
The appendix of this paper includes the faculty report by Appell, Poincare, J. Boussinesq.
This report is somewhat critical of the institution used, but praises the originality of this type of probability theory [p 349]:
“The manner in which M. Bachelier deduces Gauss’s law is very original, and all the more interesting in that his reasoning can be extended with a few changes to the theory of errors. … In fact, the author makes a comparison with the analytic theory of heat flow. A bit of thought shows that the analogy is real and the comparison is legitimate. The reasoning of Fourier, almost without change, is applicable to this problem so different from the one for which it was originally created. It is regrettable that M. Bachelier did not develop this part of his thesis further. He could have entered into the details of Fourier’s analysis. He did, however, say enough about it to justify Gauss’s law and to foresee cases where it would no longer hold.
Once Gauss’s law is established, one can easily deduce certain consequences susceptible to experimental verification. Such an example is the relation between the value of an option and the deviation from the underlying. One should not expect a very exact verification. The principle of the mathematical expectation holds in the sense that, if it were violated, there would always be people who would act so as to re-establish it and they would eventually notice this. But they would only notice it if the deviations were considerable. The verification, then, can only be gross. The author of the thesis gives statistics where this happens in a very satisfactory manner.
…
In summary, we are of the opinion that there is reason to authorize M. Bachelier tohave his thesis printed and to submit it.”
1 February, 2010 at 4:53 pm
Anonymous
Dear Prof. Tao, there seem to be two typos
between Exercise 4 and Remark 8: “dmiensional”, “ebcause”.
[Corrected, thanks – T.]
2 February, 2010 at 1:34 pm
254A, Notes 4: The semi-circular law « What’s new
[…] transform method, together with a third (heuristic) method based on Dyson Brownian motion (Notes 3b). In the next set of notes we shall also study the free probability method, and in the set of notes […]
18 February, 2010 at 11:04 am
Ben
Hi Terry,
I think there’s a link problem. These notes, Notes 3b: Brownian motion and Dyson Brownian motion seem to be the the same as the notes on eigenvalues, Notes 3b (and don’t mention Dyson’s BM at all). I was able to access the notes yesterday but not today. I’m not sure if this problem is specific to me.
[Whoops, this was caused by a bad edit on my part. Corrected, thanks. -T.]
23 February, 2010 at 12:24 am
Mio
In fractal construction, in order for to have variance
to have variance  , shouldn’t
, shouldn’t  have variance 1/2 and not 1/4 (same for
have variance 1/2 and not 1/4 (same for 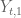 below, 1/4 instead of 1/8)?
below, 1/4 instead of 1/8)?
23 February, 2010 at 8:03 am
Terence Tao
Well, already has a variance of
already has a variance of  , so one only needs an additional variance of
, so one only needs an additional variance of 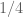 from
from  to balance it.
to balance it.
23 February, 2010 at 8:14 am
Mio
Oops, sorry. Thanks for a great lecture.
23 February, 2010 at 8:15 am
Ben
23 February, 2010 at 3:43 pm
Alex Bloemendal
Great lecture. The proof of the Ginibre formula (12) for the eigenvalue density of a GUE matrix given in Dyson’s original paper is perhaps even simpler than the one you present. Dyson adds the Ornstein-Uhlenbeck restoring term to the matrix entry processes, which just adds the same term to the induced eigenvalue processes. The matrix evolution then has GUE as its unique stationary distribution; on the other hand, we can obtain the corresponding stationary distribution for the eigenvalues as the unique probability density that is a stationary solution of the resulting modified Dyson PDE (6), which is easily seen to be (12).
I do realize this comment boils down to Exercise 11, but thought it was worth mentioning anyway — because the argument is physically compelling, and because you did introduce the Ornstein-Uhlenbeck process.
By the way, while Exercise 5 is internally consistent, your definition of Ornstein-Uhlenbeck is off from the usual one by a time-change — it has the wrong quadratic variation! I guess this is the source of the extra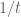 factor that appears in the definition of the generator
factor that appears in the definition of the generator  (which, incidentally, is not self-adjoint!).
(which, incidentally, is not self-adjoint!).
23 February, 2010 at 10:50 pm
Terence Tao
Thanks for the corrections and comments! It’s true that the Ornstein-Uhlenbeck approach is slightly more efficient to get the Ginibre formula, but I like the heat equation approach as it also gives the Johansson formula quite easily. Though of course, as you say, the two approaches are simply rescalings of each other, so the differences are minor.
23 February, 2010 at 5:20 pm
Alex Bloemendal
A comment regarding Remark 9:
Two-dimensional Brownian motion almost surely never hits a given point
almost surely never hits a given point 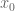 after time 0. My favourite proof uses the interpretation of certain harmonic functions as hitting probabilities, together with the form of the Green’s function of the 2-d Laplacian, to establish the following fact. Surround
after time 0. My favourite proof uses the interpretation of certain harmonic functions as hitting probabilities, together with the form of the Green’s function of the 2-d Laplacian, to establish the following fact. Surround 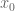 with concentric circles
with concentric circles 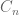 of radii
of radii 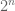 for all
for all  ; then the sequence of indices of the successive circles hit by
; then the sequence of indices of the successive circles hit by  (ignoring immediate repetition) forms a simple random walk on
(ignoring immediate repetition) forms a simple random walk on 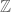 ! In particular,
! In particular,  must return to
must return to 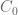 at arbitrarily large times, in between any two of which it can visit only finitely many
at arbitrarily large times, in between any two of which it can visit only finitely many 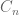 ‘s. (This argument actually establishes neighbourhood recurrence as well, since
‘s. (This argument actually establishes neighbourhood recurrence as well, since  must also hit each small circle at arbitrarily large times.)
must also hit each small circle at arbitrarily large times.)
Like everyone here, I seriously appreciate your wonderful notes and all the time you spend interacting with your readers.
23 February, 2010 at 10:02 pm
254A, Notes 6: Gaussian ensembles « What’s new
[…] have already shown using Dyson Brownian motion in Notes 3b that we have the Ginibre […]
5 March, 2010 at 1:47 pm
254A, Notes 7: The least singular value « What’s new
[…] so we expect each to have magnitude about . This, together with the Hoeffman-Wielandt inequality (Notes 3b) means that we expect to differ by from . In principle, this gives us asymptotic universality on […]
12 March, 2010 at 6:37 pm
Anonymous
Dear Prof. Tao,
Can we define Brownian motion on an infinite dimensional vector space?
a second question :we know that has mean zero and variance is
has mean zero and variance is 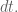 therefore
therefore 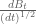 has variance 1. but why do we have
has variance 1. but why do we have 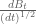 be of
be of 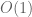 ?
?
thanks
14 March, 2010 at 12:17 am
Terence Tao
Well, there are no non-trivial unitarily invariant probability distributions on a Hilbert space (each coordinate would almost surely be zero), so one has to give up either isotropy or finite norm in order to have a meaningful infinite-dimensional Brownian motion. Of course, once one gives up either, one can certainly define Brownian-like motions (e.g. by picking an orthonormal basis and placing an independent weighted copy of Brownian motion in each coordinate).
13 March, 2010 at 9:42 pm
student
Dear Prof. Tao,
We can consider Brownian motion as a random variable from a probability space to![C([0,T]\rightarrow {\mathbb R})](https://s0.wp.com/latex.php?latex=C%28%5B0%2CT%5D%5Crightarrow+%7B%5Cmathbb+R%7D%29&bg=ffffff&fg=545454&s=0&c=20201002)
Do we have a Markov process which can be considered as a random variable from a probability space to![C^{\infty}([0,T]\rightarrow {\mathbb R})](https://s0.wp.com/latex.php?latex=C%5E%7B%5Cinfty%7D%28%5B0%2CT%5D%5Crightarrow+%7B%5Cmathbb+R%7D%29&bg=ffffff&fg=545454&s=0&c=20201002)
thanks
14 March, 2010 at 12:22 am
Terence Tao
It depends a little on how one defines the “present state” of the system, but using a naive notion of the Markov property, the right-derivative would need to be independent of the left-derivative at time t when the position at t is fixed. But for a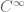 function, these two derivatives are equal, and thus must be determined completely by the position at t. This suggests to me (from the Picard uniqueness theorem) that the only processes of this type are the deterministic ones, though there is the loophole that the derivative is not required to depend in a Lipschitz manner on the position.
function, these two derivatives are equal, and thus must be determined completely by the position at t. This suggests to me (from the Picard uniqueness theorem) that the only processes of this type are the deterministic ones, though there is the loophole that the derivative is not required to depend in a Lipschitz manner on the position.
14 March, 2010 at 6:22 am
beginner
but the same argument should apply the continuous case as well. on the other hand we know that Brownian motion is a Markov process and has continuous paths. Maybe I am missing a point.
thanks
14 March, 2010 at 10:15 am
Terence Tao
Continuous paths need not have left or right derivatives.
30 January, 2011 at 1:23 pm
Carl Mueller
Usually the sigma-fields are assumed to be right continuous, meaning that the current state contains information about the infinitesimal future. So the right hand derivative (if it existed) would be part of the current state.
4 April, 2010 at 7:57 am
Dyson’s Brownian Motion « Rochester Probability Blog
[…] Dyson’s Brownian Motion Filed under: Uncategorized — carl0mueller @ 3:57 pm Tags: background See also: Tao’s blog on Dyson’s Brownian motion […]
27 January, 2011 at 2:15 pm
Minyu
Hi, Professor Tao:
There is a constant missing in the Ginibre formula and Exercise 9. It’s the reciprocal of a product of some factorials…
[Corrected, thanks – T.]
30 January, 2011 at 12:52 pm
yucao
Is it possible to extend the Brownian motion on the whole
on the whole  , i.e.
, i.e.  ?
?
15 July, 2011 at 9:59 am
Dyson Brownian Motion | Research Notebook
[…] main source for the material in this post is Terry Tao‘s set of lecture notes on Random Matrix Theory, though I also used Mehta (2004) and Anderson, Guinnet and Zeitouni (2009) as […]
21 August, 2011 at 9:36 am
On Understanding Probability Puzzles | Nair Research Notes
[…] by , from an experimental point of view. The formal construction for the Brownian motion can be found here for example. And you will get a good historical perspective of the Brownian motion here. One of the […]
18 November, 2011 at 2:38 am
Diffusion in Ehrenfest wind-tree model « Disquisitiones Mathematicae
[…] the “justification” of the word “abnormal” comes by comparison with Brownian motion and/or central limit theorem: once we know that the diffusion is “sublinear” (maybe […]
18 January, 2012 at 12:12 pm
Anonymous
Hi prof. Tau,
Thanks for these great notes!
Maybe this question is much too late, but I’d be very grateful for a reply. I’m used to think about the eigenvalues of the GUE as being subjected to a quadratic confining potential and mutual log repulsion: is there an easy way to understand the absence of the effect of the confining potential (which would give rise to a simple harmonic restoring force for each eigenvalue) in the formula for the Dyson Brownian motion, equation (5)?
Thanks for a great blog!
18 January, 2012 at 6:09 pm
Terence Tao
One can restore the confining potential by adding a term to the equation for
term to the equation for  , turning the Dyson Brownian motion to a Dyson Ornstein-Uhlenbeck process. This has the effect of keeping the variance of the matrix entries in the process constant, instead of growing linearly in time as is done here.
, turning the Dyson Brownian motion to a Dyson Ornstein-Uhlenbeck process. This has the effect of keeping the variance of the matrix entries in the process constant, instead of growing linearly in time as is done here.
The two processes (normalised variance and non-normalised variance) can be easily rescaled to each other, so the choice of which one to use is basically a matter of taste.
1 May, 2012 at 10:52 am
alabair
I am amazed by the surprising number of knowledge that is difficult to me to digest. And by the way, I would like to hear about a white noise process. Good luck.
11 November, 2012 at 1:09 pm
A direct proof of the stationarity of the Dyson sine process under Dyson Brownian motion « What’s new
[…] of a Hermitian matrix under independent Brownian motion of its entries, and is discussed in this previous blog post. To cut a long story short, this stationarity tells us that the self-similar -point correlation […]
4 February, 2013 at 2:10 am
hera
Great lecture! Prof. Tao, do you have ideas to simulate the Dyson’s brownian motion ? I’d like to do a computer simulation with MATLAB, can you give me some ideas?
5 February, 2013 at 2:47 pm
Some notes on Bakry-Emery theory « What’s new
[…] is a stochastic process with initial probability distribution ; see for instance this previous blog post for more […]
8 February, 2013 at 5:47 pm
The Harish-Chandra-Itzykson-Zuber integral formula « What’s new
[…] motion (as well as the closely related formulae for the GUE ensemble), which were derived in this previous blog post. Both of these approaches can be found in several places in the literature (and I do not actually […]
24 April, 2014 at 12:39 am
Sticky Brownian Motion | Eventually Almost Everywhere
[…] 254A, Notes 3b: Brownian motion and Dyson Brownian motion (terrytao.wordpress.com) […]
25 December, 2014 at 3:31 pm
Ramis Movassagh
Dear Terry,
Thank you for the wonderful post (your posts are always a joy to read and learn from).
Shouldn’t Prop. 2 end with “…same distribution at X_t” instead of \mu?
Best, – Ramis
[Corrected, thanks – T.]
25 December, 2014 at 6:37 pm
Ramis Movassagh
Hi Terry, Same with Prop 3. Thanks for the great post.
cheers, -R
[Corrected, thanks – T.]
7 January, 2016 at 12:45 pm
Ito Calculus by peatar | wanikanidailyscience
[…] Warning: I don’t really know much about financial mathematics so if there are any economists around: Let me know about eventual mistakes. Sources: Links in the text and Terry Tao’s blog. […]
8 November, 2017 at 12:24 am
Student
Dear Professor Tao, has O(
has O( ) third moment, but the constant of the big order should be O(
) third moment, but the constant of the big order should be O( ). Upon doing the conditioning I think one should check
). Upon doing the conditioning I think one should check  has finite third moment, but how can I do that?
has finite third moment, but how can I do that?
In the last part Theorem 6,
thanks
8 November, 2017 at 3:27 pm
Terence Tao
Actually, the third derivative scales like , so one only needs to control the second moment, not the third. The probability that two eigenvalues are within
, so one only needs to control the second moment, not the third. The probability that two eigenvalues are within  of each other is bounded by
of each other is bounded by  (this is because the Vandermonde determinant is
(this is because the Vandermonde determinant is 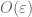 ), where we allow implied constants to depend on
), where we allow implied constants to depend on  . So the second moment is finite.
. So the second moment is finite.
11 November, 2017 at 12:19 am
Student
By the independence of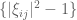 , product of two or three random variables will have zero expectation, so
, product of two or three random variables will have zero expectation, so
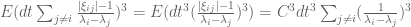 .
. be derived by direct computation? or there is some relation I need to use?
be derived by direct computation? or there is some relation I need to use?
Can the term
The of Vandermonde determinant and the process is derived in Exercise 6 and Theorem 6.
Will Using it to discuss the gap between the eigenvalues lead to circular argument(because it is a part of proof of Theorem 6)?
11 November, 2017 at 9:50 am
Terence Tao
You are right, the third moment bound is a bit too strong. I have rewritten the argument to only claim the second moment bound (for one error term) and an L^1 bound (for the other error term), which still suffices.
29 May, 2018 at 9:30 am
246C notes 4: Brownian motion, conformal invariance, and SLE | What's new
[…] and complex Brownian motions exist from any base point or ; see e.g. this previous blog post for a construction. We have the following simple […]
24 August, 2020 at 4:37 pm
Yixuan Zhou
Dear Professor Tao, I want to ask whether we can take the derivatives of the eigenvalues when we are trying to prove the Dyson Brownian Motion’s equation. I know from a previous note you justified the smoothness when the matrix process that we obtained is smooth with respect to time. However, it is not clear to me that Hermitian matrix valued BM is smooth.
31 August, 2020 at 5:00 pm
Terence Tao
The eigenvalues of a DBM will not be classically differentiable, but one can still manipulate their time derivative by the usual tools of stochastic differential calculus (in particular Ito calculus).
14 September, 2020 at 3:13 pm
Student
Dear Professor Tao,
I have a question about the last part where we derive the Johansson formula. I don’t think I am understanding the argument of extending the probability density function symmetrically from the Weyl chamber to the whole space. The questions that lingers are, first what do you mean by extending a function symmetrically. And second, why would we sum up the different initial starting location if the eigenvalues should be non-crossing.
Thanks in advance!
[See https://en.wikipedia.org/wiki/Symmetric_function ]
6 February, 2021 at 4:43 am
Anonymous
Don’t the eigenvalues of a GUE sample lie on a disk of unit radius, i.e. Girko’s law?
[The circular law of Girko is for non-Hermitian random matrices such as the Ginibre ensemble, whereas the GUE ensemble (which shoudl not be confused with the Ginibre ensemble) is Hermitian. -T]