In preparation for my upcoming course on random matrices, I am briefly reviewing some relevant foundational aspects of probability theory, as well as setting up basic probabilistic notation that we will be using in later posts. This is quite basic material for a graduate course, and somewhat pedantic in nature, but given how heavily we will be relying on probability theory in this course, it seemed appropriate to take some time to go through these issues carefully.
We will certainly not attempt to cover all aspects of probability theory in this review. Aside from the utter foundations, we will be focusing primarily on those probabilistic concepts and operations that are useful for bounding the distribution of random variables, and on ensuring convergence of such variables as one sends a parameter off to infinity.
We will assume familiarity with the foundations of measure theory; see for instance these earlier lecture notes of mine for a quick review of that topic. This is also not intended to be a first introduction to probability theory, but is instead a revisiting of these topics from a graduate-level perspective (and in particular, after one has understood the foundations of measure theory). Indeed, I suspect it will be almost impossible to follow this course without already having a firm grasp of undergraduate probability theory.
— 1. Foundations —
At a purely formal level, one could call probability theory the study of measure spaces with total measure one, but that would be like calling number theory the study of strings of digits which terminate. At a practical level, the opposite is true: just as number theorists study concepts (e.g. primality) that have the same meaning in every numeral system that models the natural numbers, we shall see that probability theorists study concepts (e.g. independence) that have the same meaning in every measure space that models a family of events or random variables. And indeed, just as the natural numbers can be defined abstractly without reference to any numeral system (e.g. by the Peano axioms), core concepts of probability theory, such as random variables, can also be defined abstractly, without explicit mention of a measure space; we will return to this point when we discuss free probability later in this course.
For now, though, we shall stick to the standard measure-theoretic approach to probability theory. In this approach, we assume the presence of an ambient sample space , which intuitively is supposed to describe all the possible outcomes of all the sources of randomness that one is studying. Mathematically, this sample space is a probability space
– a set
, together with a
-algebra
of subsets of
(the elements of which we will identify with the probabilistic concept of an event), and a probability measure
on the space of events, i.e. an assignment
of a real number in
to every event
(known as the probability of that event), such that the whole space
has probability
, and such that
is countably additive.
Elements of the sample space will be denoted
. However, for reasons that will be explained shortly, we will try to avoid actually referring to such elements unless absolutely required to.
If we were studying just a single random process, e.g. rolling a single die, then one could choose a very simple sample space – in this case, one could choose the finite set , with the discrete
-algebra
and the uniform probability measure. But if one later wanted to also study additional random processes (e.g. supposing one later wanted to roll a second die, and then add the two resulting rolls), one would have to change the sample space (e.g. to change it now to the product space
). If one was particularly well organised, one could in principle work out in advance all of the random variables one would ever want or need, and then specify the sample space accordingly, before doing any actual probability theory. In practice, though, it is far more convenient to add new sources of randomness on the fly, if and when they are needed, and extend the sample space as necessary. This point is often glossed over in introductory probability texts, so let us spend a little time on it. We say that one probability space
extends another
if there is a surjective map
which is measurable (i.e.
for every
) and probability preserving (i.e.
for every
). (Strictly speaking, it is the pair
which is the extension of
, not just the space
, but let us abuse notation slightly here.) By definition, every event
in the original probability space is canonically identified with an event
of the same probability in the extension.
Example 1 As mentioned earlier, the sample space
, that models the roll of a single die, can be extended to the sample space
that models the roll of the original die together with a new die, with the projection map
being given by
.
Another example of an extension map is that of a permutation – for instance, replacing the sample space
by the isomorphic space
by mapping
to
, etc. This extension is not actually adding any new sources of randomness, but is merely reorganising the existing randomness present in the sample space.
In order to have the freedom to perform extensions every time we need to introduce a new source of randomness, we will try to adhere to the following important dogma: probability theory is only “allowed” to study concepts and perform operations which are preserved with respect to extension of the underlying sample space. (This is analogous to how differential geometry is only “allowed” to study concepts and perform operations that are preserved with respect to coordinate change, or how graph theory is only “allowed” to study concepts and perform operations that are preserved with respect to relabeling of the vertices, etc..) As long as one is adhering strictly to this dogma, one can insert as many new sources of randomness (or reorganise existing sources of randomness) as one pleases; but if one deviates from this dogma and uses specific properties of a single sample space, then one has left the category of probability theory and must now take care when doing any subsequent operation that could alter that sample space. This dogma is an important aspect of the probabilistic way of thinking, much as the insistence on studying concepts and performing operations that are invariant with respect to coordinate changes or other symmetries is an important aspect of the modern geometric way of thinking. With this probabilistic viewpoint, we shall soon see the sample space essentially disappear from view altogether, after a few foundational issues are dispensed with.
Let’s give some simple examples of what is and what is not a probabilistic concept or operation. The probability of an event is a probabilistic concept; it is preserved under extensions. Similarly, boolean operations on events such as union, intersection, and complement are also preserved under extensions and are thus also probabilistic operations. The emptiness or non-emptiness of an event
is also probabilistic, as is the equality or non-equality of two events
(note how it was important here that we demanded the map
to be surjective in the definition of an extension). On the other hand, the cardinality of an event is not a probabilistic concept; for instance, the event that the roll of a given die gives
has cardinality one in the sample space
, but has cardinality six in the sample space
when the values of an additional die are used to extend the sample space. Thus, in the probabilistic way of thinking, one should avoid thinking about events as having cardinality, except to the extent that they are either empty or non-empty.
Indeed, once one is no longer working at the foundational level, it is best to try to suppress the fact that events are being modeled as sets altogether. To assist in this, we will choose notation that avoids explicit use of set theoretic notation. For instance, the union of two events will be denoted
rather than
, and will often be referred to by a phrase such as “the event that at least one of
or
holds”. Similarly, the intersection
will instead be denoted
, or “the event that
and
both hold”, and the complement
will instead be denoted
, or “the event that
does not hold” or “the event that
fails”. In particular the sure event
can now be referred to without any explicit mention of the sample space as
. We will continue to use the subset notation
(since the notation
may cause confusion), but refer to this statement as “
is contained in
” or “
implies
” or “
holds only if
holds” rather than “
is a subset of
“, again to downplay the role of set theory in modeling these events.
We record the trivial but fundamental union bound
for any finite or countably infinite collection of events . Taking complements, we see that if each event
fails with probability at most
, then the joint event
fails with probability at most
. Thus, if one wants to ensure that all the events
hold at once with a reasonable probability, one can try to do this by showing that the failure rate of the individual
is small compared to the number of events one is controlling. This is a reasonably efficient strategy so long as one expects the events
to be genuinely “different” from each other; if there are plenty of repetitions, then the union bound is poor (consider for instance the extreme case when
does not even depend on
).
We will sometimes refer to use of the union bound to bound probabilities as the zeroth moment method, to contrast it with the first moment method, second moment method, exponential moment method, and Fourier moment methods for bounding probabilities that we will encounter later in this course.
Let us formalise some specific cases of the union bound that we will use frequently in the course. In most of this course, there will be an integer parameter , which will often be going off to infinity, and upon which most other quantities will depend; for instance, we will often be considering the spectral properties of
random matrices.
Definition 1 (Asymptotic notation) We use
,
,
, or
to denote the estimate
for some
independent of
and all
. If we need
to depend on a parameter, e.g.
, we will indicate this by subscripts, e.g.
. We write
if
for some
that goes to zero as
. We write
or
if
.
Given an event depending on such a parameter
, we have five notions (in decreasing order of confidence) that an event is likely to hold:
- An event
holds surely (or is true) if it is equal to the sure event
.
- An event
holds almost surely (or with full probability) if it occurs with probability
:
.
- An event
holds with overwhelming probability if, for every fixed
, it holds with probability
(i.e. one has
for some
independent of
).
- An event
holds with high probability if it holds with probability
for some
independent of
(i.e. one has
for some
independent of
).
- An event
holds asymptotically almost surely if it holds with probability
, thus the probability of success goes to
in the limit
.
Of course, all of these notions are probabilistic notions.
Given a family of events depending on some parameter
, we say that each event in the family holds with overwhelming probability uniformly in
if the constant
in the definition of overwhelming probability is independent of
; one can similarly define uniformity in the concepts of holding with high probability or asymptotic almost sure probability.
From the union bound (1) we immediately have
- If
is an arbitrary family of events that each hold surely, then
holds surely.
- If
is an at most countable family of events that each hold almost surely, then
holds almost surely.
- If
is a family of events of polynomial cardinality (i.e. cardinality
) which hold with uniformly overwhelming probability, the
holds with overwhelming probability.
- If
is a family of events of sub-polynomial cardinality (i.e. cardinality
) which hold with uniformly high probability, the
holds with high probability. (In particular, the cardinality can be polylogarithmic in size,
.)
- If
is a family of events of uniformly bounded cardinality (i.e. cardinality
) which each hold asymptotically almost surely, then
holds asymptotically almost surely. (Note that uniformity of asymptotic almost sureness is automatic when the cardinality is bounded.)
Note how as the certainty of an event gets stronger, the number of times one can apply the union bound increases. In particular, holding with overwhelming probability is practically as good as holding surely or almost surely in many of our applications (except when one has to deal with the entropy of an -dimensional system, which can be exponentially large, and will thus require a certain amount of caution).
— 2. Random variables —
An event can be in just one of two states: the event can hold or fail, with some probability assigned to each. But we will usually need to consider the more general class of random variables which can be in multiple states.
Definition 3 (Random variable) Let
be a measurable space (i.e. a set
, equipped with a
-algebra of subsets of
). A random variable taking values in
(or an
-valued random variable) is a measurable map
from the sample space to
, i.e. a function
such that
is an event for every
.
As the notion of a random variable involves the sample space, one has to pause to check that it invariant under extensions before one can assert that it is a probabilistic concept. But this is clear: if is a random variable, and
is an extension of
, then
is also a random variable, which generates the same events in the sense that
for every
.
At this point let us make the convenient convention (which we have in fact been implicitly using already) that an event is identified with the predicate which is true on the event set and false outside of the event set. Thus for instance the event could be identified with the predicate “
“; this is preferable to the set-theoretic notation
, as it does not require explicit reference to the sample space and is thus more obviously a probabilistic notion. We will often omit the quotes when it is safe to do so, for instance
is shorthand for
.
Remark 1 On occasion, we will have to deal with almost surely defined random variables, which are only defined on a subset
of
of full probability. However, much as measure theory and integration theory is largely unaffected by modification on sets of measure zero, many probabilistic concepts, in particular probability, distribution, and expectation, are similarly unaffected by modification on events of probability zero. Thus, a lack of definedness on an event of probability zero will usually not cause difficulty, so long as there are at most countably many such events in which one of the probabilistic objects being studied is undefined. In such cases, one can usually resolve such issues by setting a random variable to some arbitrary value (e.g.
) whenever it would otherwise be undefined.
We observe a few key subclasses and examples of random variables:
- Discrete random variables, in which
is the discrete
-algebra, and
is at most countable. Typical examples of
include a countable subset of the reals or complexes, such as the natural numbers or integers. If
, we say that the random variable is Boolean, while if
is just a singleton set
we say that the random variable is deterministic, and (by abuse of notation) we identify this random variable with
itself. Note that a Boolean random variable is nothing more than an indicator function
of an event
, where
is the event that the boolean function equals
.
- Real-valued random variables, in which
is the real line and
is the Borel
-algebra, generated by the open sets of
. Thus for any real-valued random variable
and any interval
, we have the events “
“. In particular, we have the upper tail event “
” and lower tail event “
” for any threshold
. (We also consider the events “
” and “
” to be tail events; in practice, there is very little distinction between the two.)
- Complex random variables, whose range is the complex plane with the Borel
-algebra. A typical event associated to a complex random variable
is the small ball event “
” for some complex number
and some (small) radius
. We refer to real and complex random variables collectively as scalar random variables.
- Given a
-valued random variable
, and a measurable map
, the
-valued random variable
is indeed a random variable, and the operation of converting
to
is preserved under extension of the sample space and is thus probabilistic. This variable
can also be defined without reference to the sample space as the unique random variable for which the identity
holds for all
-measurable sets
.
- Given two random variables
and
taking values in
respectively, one can form the joint random variable
with range
with the product
-algebra, by setting
for every
. One easily verifies that this is indeed a random variable, and that the operation of taking a joint random variable is a probabilistic operation. This variable can also be defined without reference to the sample space as the unique random variable for which one has
and
, where
and
are the usual projection maps from
to
respectively. One can similarly define the joint random variable
for any family of random variables
in various ranges
(note here that the set
of labels can be infinite or even uncountable).
- Combining the previous two constructions, given any measurable binary operation
and random variables
taking values in
respectively, one can form the
-valued random variable
, and this is a probabilistic operation. Thus for instance one can add or multiply together scalar random variables, and similarly for the matrix-valued random variables that we will consider shortly. Similarly for ternary and higher order operations. A technical issue: if one wants to perform an operation (such as division of two scalar random variables) which is not defined everywhere (e.g. division when the denominator is zero). In such cases, one has to adjoin an additional “undefined” symbol
to the output range
. In practice, this will not be a problem as long as all random variables concerned are defined (i.e. avoid
) almost surely.
- Vector-valued random variables, which take values in a finite-dimensional vector space such as
or
with the Borel
-algebra. One can view a vector-valued random variable
as the joint random variable of its scalar component random variables
.
- Matrix-valued random variables or random matrices, which take values in a space
or
of
real or complex-valued matrices, again with the Borel
-algebra, where
are integers (usually we will focus on the square case
). Note here that the shape
of the matrix is deterministic; we will not consider in this course matrices whose shapes are themselves random variables. One can view a matrix-valued random variable
as the joint random variable of its scalar components
. One can apply all the usual matrix operations (e.g. sum, product, determinant, trace, inverse, etc.) on random matrices to get a random variable with the appropriate range, though in some cases (e.g with inverse) one has to adjoin the undefined symbol
as mentioned earlier.
- Point processes, which take values in the space
of subsets
of a space
(or more precisely, on the space of multisets of
, or even more precisely still as integer-valued locally finite measures on
), with the
-algebra being generated by the counting functions
for all precompact measurable sets
. Thus, if
is a point process in
, and
is a precompact measurable set, then the counting function
is a discrete random variable in
. For us, the key example of a point process comes from taking the spectrum
of eigenvalues (counting multiplicity) of a random
matrix
. I discuss point processes further in this previous blog post. We will return to point processes (and define them more formally) later in this course.
Remark 2 A pedantic point: strictly speaking, one has to include the range
of a random variable
as part of that variable (thus one should really be referring to the pair
rather than
). This leads to the annoying conclusion that, technically, boolean random variables are not integer-valued, integer-valued random variables are not real-valued, and real-valued random variables are not complex-valued. To avoid this issue we shall abuse notation very slightly and identify any random variable
to any coextension
of that random variable to a larger range space
(assuming of course that the
-algebras are compatible). Thus, for instance, a real-valued random variable which happens to only take a countable number of values will now be considered a discrete random variable also.
Given a random variable taking values in some range
, we define the distribution
of
to be the probability measure on the measurable space
defined by the formula
thus is the pushforward
of the sample space probability measure
by
. This is easily seen to be a probability measure, and is also a probabilistic concept. The probability measure
is also known as the law for
.
We write for
; we also abuse notation slightly by writing
.
We have seen that every random variable generates a probability distribution . The converse is also true:
Lemma 4 (Creating a random variable with a specified distribution) Let
be a probability measure on a measurable space
. Then (after extending the sample space
if necessary) there exists an
-valued random variable
with distribution
.
Proof: Extend to
by using the obvious projection map
from
back to
, and extending the probability measure
on
to the product measure
on
. The random variable
then has distribution
.
In the case of discrete random variables, is the discrete probability measure
where are non-negative real numbers that add up to
. To put it another way, the distribution of a discrete random variable can be expressed as the sum of Dirac masses:
We list some important examples of discrete distributions:
- Dirac distributions
, in which
for
and
otherwise;
- discrete uniform distributions, in which
is finite and
for all
;
- (Unsigned) Bernoulli distributions, in which
,
, and
for some parameter
;
- The signed Bernoulli distribution, in which
and
;
- Lazy signed Bernoulli distributions, in which
,
, and
for some parameter
;
- Geometric distributions, in which
and
for all natural numbers
and some parameter
; and
- Poisson distributions, in which
and
for all natural numbers
and some parameter
.
Now we turn to non-discrete random variables taking values in some range
. We say that a random variable is continuous if
for all
(here we assume that all points are measurable). If
is already equipped with some reference measure
(e.g. Lebesgue measure in the case of scalar, vector, or matrix-valued random variables), we say that the random variable is absolutely continuous if
for all null sets
in
. By the Radon-Nikodym theorem, we can thus find a non-negative, absolutely integrable function
with
such that
for all measurable sets . More succinctly, one has
We call the probability density function of the probability distribution
(and thus, of the random variable
). As usual in measure theory, this function is only defined up to almost everywhere equivalence, but this will not cause any difficulties.
In the case of real-valued random variables , the distribution
can also be described in terms of the cumulative distribution function
Indeed, is the Lebesgue-Stieltjes measure of
, and (in the absolutely continuous case) the derivative of
exists and is equal to the probability density function almost everywhere. We will not use the cumulative distribution function much in this course, although we will be very interested in bounding tail events such as
or
.
We give some basic examples of absolutely continuous scalar distributions:
- uniform distributions, in which
for some subset
of the reals or complexes of finite non-zero measure, e.g. an interval
in the real line, or a disk in the complex plane.
- The real normal distribution
of mean
and variance
, given by the density function
for
. We isolate in particular the standard (real) normal distribution
. Random variables with normal distributions are known as gaussian random variables.
- The complex normal distribution
of mean
and variance
, given by the density function
. Again, we isolate the standard complex normal distribution
.
Later on, we will encounter several more scalar distributions of relevance to random matrix theory, such as the semicircular law or Marcenko-Pastur law. We will also of course encounter many matrix distributions (also known as matrix ensembles) as well as point processes.
Given an unsigned random variable (i.e. a random variable taking values in
), one can define the expectation or mean
as the unsigned integral
which by the Fubini-Tonelli theorem can also be rewritten as
The expectation of an unsigned variable lies in also . If
is a scalar random variable (which is allowed to take the value
) for which
, we say that
is absolutely integrable, in which case we can define its expectation as
in the complex case. Similarly for vector-valued random variables (note that in finite dimensions, all norms are equivalent, so the precise choice of norm used to define is not relevant here). If
is a vector-valued random variable, then
is absolutely integrable if and only if the components
are all absolutely integrable, in which case one has
.
A deterministic scalar random variable is its own mean. An indicator function
has mean
. An unsigned Bernoulli variable (as defined previously) has mean
, while a signed or lazy signed Bernoulli variable has mean
. A real or complex gaussian variable with distribution
has mean
. A Poisson random variable has mean
; a geometric random variable has mean
. A uniformly distributed variable on an interval
has mean
.
A fundamentally important property of expectation is that it is linear: if are absolutely integrable scalar random variables and
are finite scalars, then
is also absolutely integrable and
By the Fubini-Tonelli theorem, the same result also applies to infinite sums provided that
is finite.
We will use linearity of expectation so frequently in the sequel that we will often omit an explicit reference to it when it is being used. It is important to note that linearity of expectation requires no assumptions of independence or dependence amongst the individual random variables ; this is what makes this property of expectation so powerful.
In the unsigned (or real absolutely integrable) case, expectation is also monotone: if is true for some unsigned or real absolutely integrable
, then
. Again, we will usually use this basic property without explicit mentioning it in the sequel.
For an unsigned random variable, we have the obvious but very useful Markov inequality
for any , as can be seen by taking expectations of the inequality
. For signed random variables, Markov’s inequality becomes
Another fact related to Markov’s inequality is that if is an unsigned or real absolutely integrable random variable, then
must hold with positive probability, and also
must also hold with positive probability. Use of these facts or (13), (14), combined with monotonicity and linearity of expectation, is collectively referred to as the first moment method. This method tends to be particularly easy to use (as one does not need to understand dependence or independence), but by the same token often gives sub-optimal results (as one is not exploiting any independence in the system).
Exercise 1 (Borel-Cantelli lemma) Let
be a sequence of events such that
. Show that almost surely, at most finitely many of the events
occur at once. State and prove a result to the effect that the condition
cannot be weakened.
If is an absolutely integrable or unsigned scalar random variable, and
is a measurable function from the scalars to the unsigned extended reals
, then one has the change of variables formula
when is complex-valued. The same formula applies to signed or complex
if it is known that
is absolutely integrable. Important examples of expressions such as
are moments
for various (particularly
), exponential moments
for real ,
, and Fourier moments (or the characteristic function)
for complex or vector-valued , where
denotes a real inner product. We shall also occasionally encounter the resolvents
for complex , though one has to be careful now with the absolute convergence of this random variable. Similarly, we shall also occasionally encounter negative moments
of
, particularly for
. We also sometimes use the zeroth moment
, where we take the somewhat unusual convention that
for non-negative
, thus
for
and
. Thus, for instance, the union bound (1) can be rewritten (for finitely many
, at least) as
for any scalar random variables and scalars
(compare with (12)).
It will be important to know if a scalar random variable is “usually bounded”. We have several ways of quantifying this, in decreasing order of strength:
is surely bounded if there exists an
such that
surely.
is almost surely bounded if there exists an
such that
almost surely.
is subgaussian if there exist
such that
for all
.
has sub-exponential tail if there exist
such that
for all
.
has finite
moment for some
if there exists
such that
.
is absolutely integrable if
.
is almost surely finite if
almost surely.
Exercise 2 Show that these properties genuinely are in decreasing order of strength, i.e. that each property on the list implies the next.
Exercise 3 Show that each of these properties are closed under vector space operations, thus for instance if
have sub-exponential tail, show that
and
also have sub-exponential tail for any scalar
.
The various species of Bernoulli random variable are surely bounded, and any random variable which is uniformly distributed in a bounded set is almost surely bounded. Gaussians are of course subgaussian, while the Poisson and geometric distributions merely have sub-exponential tail. Cauchy distributions are typical examples of heavy-tailed distributions which are almost surely finite, but do not have all moments finite (indeed, the Cauchy distribution does not even have finite first moment).
If we have a family of scalar random variables depending on a parameter
, we say that the
are uniformly surely bounded (resp. uniformly almost surely bounded, uniformly subgaussian, have uniform sub-exponential tails, or uniformly bounded
moment) if the relevant parameters
in the above definitions can be chosen to be independent of
.
Fix . If
has finite
moment, say
, then from Markov’s inequality (14) one has
thus we see that the higher the moments that we control, the faster the tail decay is. From the dominated convergence theorem we also have the variant
However, this result is qualitative or ineffective rather than quantitative because it provides no rate of convergence of to zero. Indeed, it is easy to construct a family
of random variables of uniformly bounded
moment, but for which the quantities
do not converge uniformly to zero (e.g. take
to be
times the indicator of an event of probability
for
). Because of this issue, we will often have to strengthen the property of having a uniformly bounded moment, to that of obtaining a uniformly quantitative control on the decay in (24) for a family
of random variables; we will see examples of this in later lectures. However, this technicality does not arise in the important model case of identically distributed random variables, since in this case we trivially have uniformity in the decay rate of (24).
We observe some consequences of (23):
Lemma 5 Let
be a scalar random variable depending on a parameter
.
- If
has uniformly bounded expectation, then for any
independent of
, we have
with high probability.
- If
has uniformly bounded
moment, then for any
, we have
with probability
.
- If
has uniform sub-exponential tails, then we have
with overwhelming probability.
Exercise 4 Show that a real-valued random variable
is subgaussian if and only if there exist
such that
for all real
, and if and only if there exists
such that
for all
.
Exercise 5 Show that a real-valued random variable
has subexponential tails if and only if there exist
such that
for all positive integers
.
Once the second moment of a scalar random variable is finite, one can define the variance
From Markov’s inequality we thus have Chebyshev’s inequality
Upper bounds on for
large are known as large deviation inequality. Chebyshev’s inequality gives a simple but still useful large deviation inequality, which becomes useful once
exceeds the standard deviation
of the random variable. The use of Chebyshev’s inequality, combined with a computation of variances, is known as the second moment method.
Exercise 6 (Scaling of mean and variance) If
is a scalar random variable of finite mean and variance, and
are scalars, show that
and
. In particular, if
has non-zero variance, then there exist scalars
such that
has mean zero and variance one.
Exercise 7 We say that a real number
is a median of a real-valued random variable
if
.
- Show that a median always exists, and if
is absolutely continuous with strictly positive density function, then the median is unique.
- If
has finite second moment, show that
for any median
.
If is subgaussian (or has sub-exponential tails with exponent
), then from dominated convergence we have the Taylor expansion
for any real or complex , thus relating the exponential and Fourier moments with the
moments.
— 3. Independence —
When studying the behaviour of a single random variable , the distribution
captures all the probabilistic information one wants to know about
. The following exercise is one way of making this statement rigorous:
Exercise 8 Let
,
be random variables (on sample spaces
respectively) taking values in a range
, such that
. Show that after extending the spaces
, the two random variables
are isomorphic, in the sense that there exists a probability space isomorphism
(i.e. an invertible extension map whose inverse is also an extension map) such that
.
However, once one studies families of random variables
taking values in measurable spaces
(on a single sample space
), the distribution of the individual variables
are no longer sufficient to describe all the probabilistic statistics of interest; the joint distribution of the variables (i.e. the distribution of the tuple
, which can be viewed as a single random variable taking values in the product measurable space
) also becomes relevant.
Example 2 Let
be drawn uniformly at random from the set
. Then the random variables
,
, and
all individually have the same distribution, namely the signed Bernoulli distribution. However the pairs
,
, and
all have different joint distributions: the first pair, by definition, is uniformly distributed in
, while the second pair is uniformly distributed in
, and the third pair is uniformly distributed in
. Thus, for instance, if one is told that
are two random variables with the Bernoulli distribution, and asked to compute the probability that
, there is insufficient information to solve the problem; if
were distributed as
, then the probability would be
, while if
were distributed as
, the probability would be
, and if
were distributed as
, the probability would be
. Thus one sees that one needs the joint distribution, and not just the individual distributions, to obtain a unique answer to the question.
There is however an important special class of families of random variables in which the joint distribution is determined by the individual distributions.
Definition 6 (Joint independence) A family
of random variables (which may be finite, countably infinite, or uncountably infinite) is said to be jointly independent if the distribution of
is the product measure of the distribution of the individual
.
A family
is said to be pairwise independent if the pairs
are jointly independent for all distinct
. More generally,
is said to be
-wise independent if
are jointly independent for all
and all distinct
.
We also say that
is independent of
if
are jointly independent.
A family of events
is said to be jointly independent if their indicators
are jointly independent. Similarly for pairwise independence and
-wise independence.
From the theory of product measure, we have the following equivalent formulation of joint independence:
Exercise 9 Let
be a family of random variables, with each
taking values in a measurable space
.
- Show that the
are jointly independent if and only if for every collection of distinct elements
of
, and all measurable subsets
for
, one has
- Show that the necessary and sufficient condition
being
-wise independent is the same, except that
is constrained to be at most
.
In particular, a finite family
of random variables
,
taking values in measurable spaces
are jointly independent if and only if
for all measurable
.
If the
are discrete random variables, one can take the
to be singleton sets in the above discussion.
From the above exercise we see that joint independence implies -wise independence for any
, and that joint independence is preserved under permuting, relabeling, or eliminating some or all of the
. A single random variable is automatically jointly independent, and so
-wise independence is vacuously true; pairwise independence is the first nontrivial notion of independence in this hierarchy.
Example 3 Let
be the field of two elements, let
be the subspace of triples
with
, and let
be drawn uniformly at random from
. Then
are pairwise independent, but not jointly independent. In particular,
is independent of each of
separately, but is not independent of
.
Exercise 10 This exercise generalises the above example. Let
be a finite field, and let
be a subspace of
for some finite
. Let
be drawn uniformly at random from
. Suppose that
is not contained in any coordinate hyperplane in
.
- Show that each
,
is uniformly distributed in
.
- Show that for any
, that
is
-wise independent if and only if
is not contained in any hyperplane which is definable using at most
of the coordinate variables.
- Show that
is jointly independent if and only if
.
Informally, we thus see that imposing constraints between
variables at a time can destroy
-wise independence, while leaving lower-order independence unaffected.
Exercise 11 Let
be the subspace of triples
with
, and let
be drawn uniformly at random from
. Then
is independent of
(and in particular, is independent of
and
separately), but
are not independent of each other.
Exercise 12 We say that one random variable
(with values in
) is determined by another random variable
(with values in
) if there exists a (deterministic) function
such that
is surely true (i.e.
for all
). Show that if
is a family of jointly independent random variables, and
is a family such that each
is determined by some subfamily
of the
, with the
disjoint as
varies, then the
are jointly independent also.
Exercise 13 (Determinism vs. independence) Let
be random variables. Show that
is deterministic if and only if it is simultaneously determined by
, and independent of
.
Exercise 14 Show that a complex random variable
is a complex gaussian random variable (i.e. its distribution is a complex normal distribution) if and only if its real and imaginary parts
are independent real gaussian random variables with the same variance. In particular, the variance of
and
will be half of variance of
.
One key advantage of working with jointly independent random variables and events is that one can compute various probabilistic quantities quite easily. We give some key examples below.
Exercise 15 If
are jointly independent events, show that
Show that the converse statement (i.e. that (28) and (29) imply joint independence) is true for
, but fails for higher
. Can one find a correct replacement for this converse for higher
?
- If
are jointly independent random variables taking values in
, show that
- If
are jointly independent absolutely integrable scalar random variables, show that
is absolutely integrable, and
Remark 3 The above exercise combines well with Exercise 12. For instance, if
are jointly independent subgaussian variables, then from Exercises 12, 16 we see that
for any complex
. This identity is a key component of the exponential moment method, which we will discuss in the next set of notes.
The following result is a key component of the second moment method.
Exercise 17 (Pairwise independence implies linearity of variance) If
are pairwise independent scalar random variables of finite mean and variance, show that
and more generally
The product measure construction allows us to extend Lemma 4:
Exercise 18 (Creation of new, independent random variables) Let
be a family of random variables (not necessarily independent or finite), and let
be a collection (not necessarily finite) of probability measures
on measurable spaces
. Then, after extending the sample space if necessary, one can find a family
of independent random variables, such that each
has distribution
, and the two families
and
are independent of each other.
We isolate the important case when is independent of
. We say that a family
of random variables is independently and identically distributed, or iid for short, if they are jointly independent and all the
have the same distribution.
Corollary 7 Let
be a family of random variables (not necessarily independent or finite), let
be a probability measure on a measurable space
, and let
be an arbitrary set. Then, after extending the sample space if necessary, one can find an iid family
with distribution
which is independent of
.
Thus, for instance, one can create arbitrarily large iid families of Bernoulli random variables, Gaussian random variables, etc., regardless of what other random variables are already in play. We thus see that the freedom to extend the underyling sample space allows us access to an unlimited source of randomness. This is in contrast to a situation studied in complexity theory and computer science, in which one does not assume that the sample space can be extended at will, and the amount of randomness one can use is therefore limited.
Remark 4 Given two probability measures
on two measurable spaces
, a joining or coupling of the these measures is a random variable
taking values in the product space
, whose individual components
have distribution
respectively. Exercise 18 shows that one can always couple two distributions together in an independent manner; but one can certainly create non-independent couplings as well. The study of couplings (or joinings) is particularly important in ergodic theory, but this will not be the focus of this course.
— 4. Conditioning —
Random variables are inherently non-deterministic in nature, and as such one has to be careful when applying deterministic laws of reasoning to such variables. For instance, consider the law of the excluded middle: a statement is either true or false, but not both. If this statement is a random variable, rather than deterministic, then instead it is true with some probability
and false with some complementary probability
. Also, applying set-theoretic constructions with random inputs can lead to sets, spaces, and other structures which are themselves random variables, which can be quite confusing and require a certain amount of technical care; consider, for instance, the task of rigorously defining a Euclidean space
when the dimension
is itself a random variable.
Now, one can always eliminate these difficulties by explicitly working with points in the underlying sample space
, and replacing every random variable
by its evaluation
at that point; this removes all the randomness from consideration, making everything deterministic (for fixed
). This approach is rigorous, but goes against the “probabilistic way of thinking”, as one now needs to take some care in extending the sample space.
However, if instead one only seeks to remove a partial amount of randomness from consideration, then one can do this in a manner consistent with the probabilistic way of thinking, by introducing the machinery of conditioning. By conditioning an event to be true or false, or conditioning a random variable to be fixed, one can turn that random event or variable into a deterministic one, while preserving the random nature of other events and variables (particularly those which are independent of the event or variable being conditioned upon).
We begin by considering the simpler situation of conditioning on an event.
Definition 8 (Conditioning on an event) Let
be an event (or statement) which holds with positive probability
. By conditioning on the event
, we mean the act of replacing the underlying sample space
with the subset of
where
holds, and replacing the underlying probability measure
by the conditional probability measure
, defined by the formula
All events
on the original sample space can thus be viewed as events
on the conditioned space, which we model set-theoretically as the set of all
in
obeying
. Note that this notation is compatible with (31).
All random variables
on the original sample space can also be viewed as random variables
on the conditioned space, by restriction. We will refer to this conditioned random variable as
, and thus define conditional distribution
and conditional expectation
(if
is scalar) accordingly.
One can also condition on the complementary event
, provided that this event holds with positive probility also.
By undoing this conditioning, we revert the underlying sample space and measure back to their original (or unconditional) values. Note that any random variable which has been defined both after conditioning on
, and conditioning on
, can still be viewed as a combined random variable after undoing the conditioning.
Conditioning affects the underlying probability space in a manner which is different from extension, and so the act of conditioning is not guaranteed to preserve probabilistic concepts such as distribution, probability, or expectation. Nevertheless, the conditioned version of these concepts are closely related to their unconditional counterparts:
Exercise 19 If
and
both occur with positive probability, establish the identities
for any (unconditional) event
and
for any (unconditional) random variable
(in the original sample space). In a similar spirit, if
is a non-negative or absolutely integrable scalar (unconditional) random variable, show that
,
are also non-negative and absolutely integrable on their respective conditioned spaces, and that
In the degenerate case when
occurs with full probability, conditioning to the complementary event
is not well defined, but show that in those cases we can still obtain the above formulae if we adopt the convention that any term involving the vanishing factor
should be omitted. Similarly if
occurs with zero probability.
The above identities allow one to study probabilities, distributions, and expectations on the original sample space by conditioning to the two conditioned spaces.
From (32) we obtain the inequality
thus conditioning can magnify probabilities by a factor of at most . In particular,
- If
occurs unconditionally surely, it occurs surely conditioning on
also.
- If
occurs unconditionally almost surely, it occurs almost surely conditioning on
also.
- If
occurs unconditionally with overwhelming probability, it occurs with overwhelming probability conditioning on
also, provided that
for some
independent of
.
- If
occurs unconditionally with high probability, it occurs with high probability conditioning on
also, provided that
for some
and some sufficiently small
independent of
.
- If
occurs unconditionally asymptotically almost surely, it occurs asymptotically almost surely conditioning on
also, provided that
for some
independent of
.
Conditioning can distort the probability of events and the distribution of random variables. Most obviously, conditioning on elevates the probability of
to
, and sends the probability of the complementary event
to zero. In a similar spirit, if
is a random variable uniformly distributed on some finite set
, and
is a non-empty subset of
, then conditioning to the event
alters the distribution of
to now become the uniform distribution on
rather than
(and conditioning to the complementary event produces the uniform distribution on
).
However, events and random variables that are independent of the event being conditioned upon are essentially unaffected by conditioning. Indeed, if
is an event independent of
, then
occurs with the same probability as
; and if
is a random variable independent of
(or equivalently, independently of the indicator
), then
has the same distribution as
.
Remark 5 One can view conditioning to an event
and its complement
as the probabilistic analogue of the law of the excluded middle. In deterministic logic, given a statement
, one can divide into two separate cases, depending on whether
is true or false; and any other statement
is unconditionally true if and only if it is conditionally true in both of these two cases. Similarly, in probability theory, given an event
, one can condition into two separate sample spaces, depending on whether
is conditioned to be true or false; and the unconditional statistics of any random variable or event are then a weighted average of the conditional statistics on the two sample spaces, where the weights are given by the probability of
and its complement.
Now we consider conditioning with respect to a discrete random variable , taking values in some range
. One can condition on any event
,
which occurs with positive probability. It is then not difficult to establish the analogous identities to those in Exercise 19:
Exercise 20 Let
be a discrete random variable with range
. Then we have
for any (unconditional) event
, and
for any (unconditional) random variable
(where the sum of non-negative measures is defined in the obvious manner), and for absolutely integrable or non-negative (unconditional) random variables
, one has
In all of these identities, we adopt the convention that any term involving
is ignored when
.
With the notation as in the above exercise, we define the conditional probability of an (unconditional) event
conditioning on
to be the (unconditional) random variable that is defined to equal
whenever
, and similarly, for any absolutely integrable or non-negative (unconditional) random variable
, we define the conditional expectation
to be the (unconditional) random variable that is defined to equal
whenever
. (Strictly speaking, since we are not defining conditional expectation when
, these random variables are only defined almost surely, rather than surely, but this will not cause difficulties in practice; see Remark 1.) Thus (36), (38) simplify to
Remark 6 One can interpret conditional expectation as a type of orthogonal projection; see for instance these previous lecture notes of mine. But we will not use this perspective in this course. Just as conditioning on an event and its complement can be viewed as the probabilistic analogue of the law of the excluded middle, conditioning on a discrete random variable can be viewed as the probabilistic analogue of dividing into finitely or countably many cases. For instance, one could condition on the outcome
of a six-sided die, thus conditioning the underlying sample space into six separate subspaces. If the die is fair, then the unconditional statistics of a random variable or event would be an unweighted average of the conditional statistics of the six conditioned subspaces; if the die is weighted, one would take a weighted average instead.
Example 4 Let
be iid signed Bernoulli random variables, and let
, thus
is a discrete random variable taking values in
(with probability
,
,
respectively). Then
remains a signed Bernoulli random variable when conditioned to
, but becomes the deterministic variable
when conditioned to
, and similarly becomes the deterministic variable
when conditioned to
. As a consequence, the conditional expectation
is equal to
when
,
when
, and
when
; thus
. Similarly
; summing and using the linearity of (conditional) expectation (which follows automatically from the unconditional version) we obtain the obvious identity
.
If are independent, then
for all
(with the convention that those
for which
are ignored), which implies in particular (for absolutely integrable
) that
(so in this case the conditional expectation is a deterministic quantity).
Example 5 Let
be bounded scalar random variables (not necessarily independent), with
discrete. Then we have
where the latter equality holds since
clearly becomes deterministic after conditioning on
.
We will also need to condition with respect to continuous random variables (this is the probabilistic analogue of dividing into a potentially uncountable number of cases). To do this formally, we need to proceed a little differently from the discrete case, introducing the notion of a disintegration of the underlying sample space.
Definition 9 (Disintegration) Let
be a random variable with range
. A disintegration
of the underlying sample space
with respect to
is a subset
of
of full measure in
(thus
almost surely), together with assignment of a probability measure
on the subspace
of
for each
, which is measurable in the sense that the map
is measurable for every event
, and such that
for all such events, where
is the (almost surely defined) random variable defined to equal
whenever
.
Given such a disintegration, we can then condition to the event
for any
by replacing
with the subspace
(with the induced
-algebra), but replacing the underlying probability measure
with
. We can thus condition (unconditional) events
and random variables
to this event to create conditioned events
and random variables
on the conditioned space, giving rise to conditional probabilities
(which is consistent with the existing notation for this expression) and conditional expectations
(assuming absolute integrability in this conditioned space). We then set
to be the (almost surely defined) random variable defined to equal
whenever
.
Example 6 (Discrete case) If
is a discrete random variable, one can set
to be the essential range of
, which in the discrete case is the set of all
for which
. For each
, we define
to be the conditional probability measure relative to the event
, as defined in Definition 8. It is easy to verify that this is indeed a disintegration; thus the continuous notion of conditional probability generalises the discrete one.
Example 7 (Independent case) Starting with an initial sample space
, and a probability measure
on a measurable space
, one can adjoin a random variable
taking values in
with distribution
that is independent of all previously existing random variables, by extending
to
as in Lemma 4. One can then disintegrate
by taking
and letting
be the probability measure on
induced by the obvious isomorphism between
and
; this is easily seen to be a disintegration. Note that if
is any random variable from the original space
, then
has the same distribution as
for any
.
Example 8 Let
with Lebesgue measure, and let
be the coordinate random variables of
, thus
are iid with the uniform distribution on
. Let
be the random variable
with range
. Then one can disintegrate
by taking
and letting
be normalised Lebesgue measure on the diagonal line segment
.
Exercise 21 (Almost uniqueness of disintegrations) Let
,
be two disintegrations of the same random variable
. Show that for any event
, one has
for
-almost every
, where the conditional probabilities
and
are defined using the disintegrations
,
respectively. (Hint: argue by contradiction, and consider the set of
for which
exceeds
(or vice versa) by some fixed
.)
Similarly, for a scalar random variable
, show that for
-almost every
, that
is absolutely integrable with respect to the first disintegration if and only if it is absolutely integrable with respect to the second integration, and one has
in such cases.
Remark 7 Under some mild topological assumptions on the underlying sample space (and on the measurable space
), one can always find at least one disintegration for every random variable
, by using tools such as the Radon-Nikodym theorem; see Theorem 4 of these previous lecture notes of mine. In practice, we will not invoke these general results here (as it is not natural for us to place topological conditions on the sample space), and instead construct disintegrations by hand in specific cases, for instance by using the construction in Example 7.
Remark 8 Strictly speaking, disintegration is not a probabilistic concept; there is no canonical way to extend a disintegration when extending the sample space;. However, due to the (almost) uniqueness and existence results alluded to earlier, this will not be a difficulty in practice. Still, we will try to use conditioning on continuous variables sparingly, in particular containing their use inside the proofs of various lemmas, rather than in their statements, due to their slight incompatibility with the “probabilistic way of thinking”.
Exercise 22 (Fubini-Tonelli theorem) Let
be a disintegration of a random variable
taking values in a measurable space
, and let
be a non-negative (resp. absolutely integrable) scalar random variable. Show that for
-almost all
,
is a non-negative (resp. absolutely integrable) random variable, and one has the identity
where
is the (almost surely defined) random variable that equals
whenever
. (Note that one first needs to show that
is measurable before one can take the expectation.) More generally, show that
whenever
is a non-negative (resp. bounded) measurable function. (One can essentially take (42), together with the fact that
is determined by
, as a definition of the conditional expectation
, but we will not adopt this approach here.)
A typical use of conditioning is to deduce a probabilistic statement from a deterministic one. For instance, suppose one has a random variable , and a parameter
in some range
, and an event
that depends on both
and
. Suppose we know that
for every
. Then, we can conclude that whenever
is a random variable in
independent of
, we also have
, regardless of what the actual distribution of
is. Indeed, if we condition
to be a fixed value
(using the construction in Example 7, extending the underlying sample space if necessary), we see that
for each
; and then one can integrate out the conditioning using (41) to obtain the claim.
The act of conditioning a random variable to be fixed is occasionally also called freezing.
— 5. Convergence —
In a first course in undergraduate real analysis, we learn what it means for a sequence of scalars to converge to a limit
; for every
, we have
for all sufficiently large
. Later on, this notion of convergence is generalised to metric space convergence, and generalised further to topological space convergence; in these generalisations, the sequence
can lie in some other space than the space of scalars (though one usually insists that this space is independent of
).
Now suppose that we have a sequence of random variables, all taking values in some space
; we will primarily be interested in the scalar case when
is equal to
or
, but will also need to consider fancier random variables, such as point processes or empirical spectral distributions. In what sense can we say that
“converges” to a random variable
, also taking values in
?
It turns out that there are several different notions of convergence which are of interest. For us, the four most important (in decreasing order of strength) will be almost sure convergence, convergence in probability, convergence in distribution, and tightness of distribution.
Definition 10 (Modes of convergence) Let
be a
-compact, locally compact metric space (with the Borel
-algebra), and let
be a sequence of random variables taking values in
. Let
be another random variable taking values in
.
converges almost surely to
if, for almost every
,
converges to
, or equivalently
for every
.
converges in probability to
if, for every
, one has
or equivalently if
holds asymptotically almost surely for every
.
converges in distribution to
if, for every bounded continuous function
, one has
has a tight sequence of distributions if, for every
, there exists a compact subset
of
such that
for all sufficiently large
.
Remark 9 One can relax the requirement that
be a
-compact, locally compact metric space in the definitions, but then some of the nice equivalences and other properties of these modes of convergence begin to break down. In our applications, though, we will only need to consider the
-compact, locally compact metric space case. Note that all of these notions are probabilistic (i.e. they are preserved under extensions of the sample space).
Exercise 23 (Implications and equivalences) Let
be random variables taking values in a
-compact, locally compact metric space
.
- (i) Show that if
converges almost surely to
, then
converges in probability to
. (Hint: Fatou’s lemma.)
- (ii) Show that if
converges in distribution to
, then
has a tight sequence of distributions.
- (iii) Show that if
converges in probability to
, then
converges in distribution to
. (Hint: first show tightness, then use the fact that on compact sets, continuous functions are uniformly continuous.)
- (iv) Show that
converges in distribution to
if and only if
converges to
in the vague topology (i.e.
for all continuous functions
of compact support).
- (v) Conversely, if
has a tight sequence of distributions, and
is convergent in the vague topology, show that
is convergent in distribution to another random variable (possibly after extending the sample space). What happens if the tightness hypothesis is dropped?
- (vi) If
is deterministic, show that
converges in probability to
if and only if
converges in distribution to
.
- (vii) If
has a tight sequence of distributions, show that there is a subsequence of the
which converges in distribution. (This is known as Prokhorov’s theorem).
- (viii) If
converges in probability to
, show that there is a subsequence of the
which converges almost surely to
.
- (ix)
converges in distribution to
if and only if
for every open subset
of
, or equivalently if
for every closed subset
of
.
Remark 10 The relationship between almost sure convergence and convergence in probability may be clarified by the following observation. If
is a sequence of events, then the indicators
converge in probability to zero iff
as
, but converge almost surely to zero iff
as
.
Example 9 Let
be a random variable drawn uniformly from
. For each
, let
be the event that the decimal expansion of
begins with the decimal expansion of
, e.g. every real number in
lies in
. (Let us ignore the annoying
ambiguity in the decimal expansion here, as it will almost surely not be an issue.) Then the indicators
converge in probability and in distribution to zero, but do not converge almost surely.
If
is the
digit of
, then the
converge in distribution (to the uniform distribution on
, but do not converge in probability or almost surely. Thus we see that the latter two notions are sensitive not only to the distribution of the random variables, but how they are positioned in the sample space.
The limit of a sequence converging almost surely or in probability is clearly unique up to almost sure equivalence, whereas the limit of a sequence converging in distribution is only unique up to equivalence in distribution. Indeed, convergence in distribution is really a statement about the distributions rather than of the random vaariables
themselves. In particular, for convergence in distribution one does not care about how correlated or dependent the
are with respect to each other, or with
; indeed, they could even live on different sample spaces
and we would still have a well-defined notion of convergence in distribution, even though the other two notions cease to make sense (except when
is deterministic, in which case we can recover convergence in probability by Exercise 23(vi)).
Exercise 24 (Borel-Cantelli lemma) Suppose that
are random variables such that
for every
. Show that
converges almost surely to
.
Exercise 25 (Convergence and moments) Let
be a sequence of scalar random variables, and let
be another scalar random variable. Let
.
- (i) If
, show that
has a tight sequence of distributions.
- (ii) If
and
converges in distribution to
, show that
.
- (iii) If
and
converges in distribution to
, show that
.
- (iv) Give a counterexample to show that (iii) fails when
, even if we upgrade convergence in distribution to almost sure convergence.
- (v) If the
are uniformly bounded and real-valued, and
for every
, then
converges in distribution to
. (Hint: use the Weierstrass approximation theorem. Alternatively, use the analytic nature of the moment generating function
and analytic continuation.)
- (vi) If the
are uniformly bounded and complex-valued, and
for every
, then
converges in distribution to
. Give a counterexample to show that the claim fails if one only considers the cases when
.
There are other interesting modes of convergence on random variables and on distributions, such as convergence in total variation norm, in the Lévy-Prokhorov metric, or in Wasserstein metric, but we will not need these concepts in this course.

134 comments
Comments feed for this article
11 April, 2012 at 7:01 pm
Rex
When defining real-valued random variables, does one typically equip the real line with the Borel measure, or its Lebesgue completion? Does this distinction matter much in practice?
For instance, does one have to do a significant amount of extra work to check that certain random variables are Lebesgue-measurable as opposed to merely Borel-measurable?
In the definition you refer only to the Borel measure, but later on you mention some issues about pullbacks of (Lebesgue) null sets when discussing absolute continuity of random variables.
11 April, 2012 at 8:28 pm
Terence Tao
In general, the Borel sigma algebra is slightly more convenient to use than the Lebesgue sigma algebra for the _range_ of a measurable function, but the Lebesgue can be more a convenient algebra to use for the _domain_ of a measurable function. But the main advantage of Lebesgue measure, namely completeness, is more useful in measure theory than in probability theory; for most probabilistic applications one does not actually need completeness.
p.s. I don’t know what issue about pullbacks of null sets you are referring to in your comment.
11 April, 2012 at 8:32 pm
Rex
I did not really mean to say there was any “issue”, but rather just that you switched from Borel measure to Lebesgue measure in the following passage:
“Now we turn to non-discrete random variables {X} taking values in some range {R}. We say that a random variable is continuous if {{\bf P}(X=x)=0} f
or all {x \in R} (here we assume that all points are measurable). If {R} is already equipped with some reference measure {dm} (e.g. Lebesgue measure in the case of scalar, vector, or matrix-valued random variables), we say that the random variable is absolutely continuous if {{\bf P}(X \in S)=0} for all null sets {S} in {R}. ”
and it was not clear to me whether there was any significance in this switch.
11 April, 2012 at 8:43 pm
Terence Tao
Ah. I tend to use Lebesgue measure to denote both the standard measure on the Lebesgue sigma algebra, as well as its restriction to the Borel sigma algebra (which is indeed the slightly more natural sigma algebra to use in this context). (The terminology “the Borel measure on ” to denote this restriction is also in use, but somewhat less common, perhaps because it can be confused with the more general concept of a Borel measure.)
” to denote this restriction is also in use, but somewhat less common, perhaps because it can be confused with the more general concept of a Borel measure.)
17 June, 2012 at 9:41 am
frankpmurphyh
Reblogged this on algebrafm.
5 September, 2012 at 6:12 pm
Gelasio Salazar
Dear Terry,
One question about the distinction between “with high probability” and
“asymptotically almost surely”. We just got a referee report in which they
ask us to change “w.h.p.” to “a.a.s.” — since in a particular lemma, all
we can prove is that a certain event holds with probability 1 -o(1). I
would have normally used w.h.p. and a.a.s. interchangeably, but after the
referee’s remark (s/he gave your Notes as reference) I realized we need to
be more careful. In the revised version we’ll use “a.a.s.”, and I was
wondering if you were aware of other sources in which this distinction
between “overwhelming probability”, “with high probability” and
“asymptotically almost surely” is used.
Last but not least, thanks for your comprehensive notes in Probability
Theory.
5 September, 2012 at 8:21 pm
Terence Tao
“asymptotically almost surely”, when it is used in literature, invariably means 1-o(1), but for “with high probability” there is less consensus; I have seen it used for both 1-o(1) and for 1-O(n^{-c}) (though not in the same paper, of course). But given that a.a.s. is a perfectly useful and accepted notation for 1-o(1), it seems logical to me to exclusively use w.h.p for 1-O(n^{-c}) instead.
19 September, 2012 at 10:59 am
Jack
Could you give an example of your saying that “If one was particularly well organised, one could in principle work out in advance all of the random variables one would ever want or need, and then specify the sample space accordingly, before doing any actual probability theory.”?
19 September, 2012 at 11:28 am
Jack
Can one say to some degree that a random variable on
on 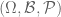 can be regarded as an extension
can be regarded as an extension 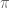 ?
?
27 September, 2012 at 5:24 pm
Jack
I’m confused about the concept “pushforward”. Let be a probability space and random variable
be a probability space and random variable  on this space with range
on this space with range 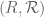 . Then
. Then 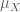 is a probability measure on
is a probability measure on 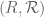 . However, according to your notes of 245A,
. However, according to your notes of 245A, 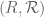 can be any measurable space, for example
can be any measurable space, for example  . But I also learned that one cannot sign a measure to
. But I also learned that one cannot sign a measure to  that render it a measure space. What do I do wrong here?
that render it a measure space. What do I do wrong here?
28 September, 2012 at 3:08 am
Terence Tao
One can place several measures on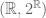 , e.g. a Dirac measure. (But one cannot have a non-trivial translation-invariant measure on this space, due to Banach-Tarski type paradoxes.)
, e.g. a Dirac measure. (But one cannot have a non-trivial translation-invariant measure on this space, due to Banach-Tarski type paradoxes.)
28 September, 2012 at 6:02 am
Jack
Ah, I see the point. As you said in this note, the underlying sample space of a random variable is often not specified. And the range of the random variable , according to Remark 2, can be somehow not mentioned either as I understand. I’m puzzled about this: to what extend should one specify a random variable? What’s left for a function when one does not specify its domain and range?
, according to Remark 2, can be somehow not mentioned either as I understand. I’m puzzled about this: to what extend should one specify a random variable? What’s left for a function when one does not specify its domain and range?
I saw lots of times when one says something like “consider a -value random variable”. They don’t even specify which
-value random variable”. They don’t even specify which  algebra is used for
algebra is used for  . What’s more, I’ve never read that one specify a measure for the range measurable space
. What’s more, I’ve never read that one specify a measure for the range measurable space  . Is it because we have an immediate one,
. Is it because we have an immediate one, 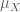 , or it doesn’t matter at all?
, or it doesn’t matter at all?
28 September, 2012 at 12:27 pm
Terence Tao
We usually don’t specify the sample space of a random variable for much the same reason we don’t specify which base (e.g. base 10, binary, etc.) we use to represent numbers, or which coordinate system we use to represent a manifold. We could specify these representations, if desired, but we wish to focus on those aspects of the mathematical objects being studied that are independent of the choice of representation, and so it is usually counterproductive to devote too much attention to these representations. (This is discussed near the beginning of this blog post.)
Also, one should make a distinction between a measurable space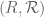 and a measure space
and a measure space 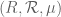 . A measurable space can be turned into a measure space by specifying a measure, but there are multiple measures one could use for this purpose, and in many cases it is better to not specify a measure at all.
. A measurable space can be turned into a measure space by specifying a measure, but there are multiple measures one could use for this purpose, and in many cases it is better to not specify a measure at all.
15 October, 2012 at 9:01 am
SAADA
Professeur Tao, auriez-vous une version française de cette note ?
Merci par avance.
15 October, 2012 at 10:08 am
Terence Tao
Non, mais outils de traduction automatique, tels que Google Translate, peuvent faire un travail raisonnable: http://translate.google.com/translate?sl=en&tl=fr&js=n&prev=_t&hl=en&ie=UTF-8&layout=2&eotf=1&u=http%3A%2F%2Fterrytao.wordpress.com%2F2010%2F01%2F01%2F254a-notes-0-a-review-of-probability-theory&act=url
15 October, 2012 at 10:35 am
Daniel
merci beaucoup professeur.
http://www.daniel-saada.eu
15 October, 2012 at 10:48 pm
Hoeffding bound | blayz
[…] first two sections of the book Topics in Random Matrix Theory by Terry Tao, with his draft and relevant notes available online, and the Hoeffding’s original paper along with the paper by […]
4 January, 2013 at 9:45 am
http terrytao wordpress com 2010 01 01 254a… « Kathys LinkBook
[…] https://terrytao.wordpress.com/2010/01/01/254a-notes-0-a-review-of-probability-theory/ […]
19 January, 2013 at 12:14 pm
tim
Hi Prof Tao,
Thanks for sharing your note!
I don’t quite understand why the extension is defined to be surjective in Tao’s blog. Is the concept “extension” trying to become morphisms in some category of probability spaces?
I found two links http://theoreticalatlas.wordpress.com/2010/11/11/categorifying-measure-theory/ and http://mathoverflow.net/questions/49426/is-there-a-category-structure-one-can-place-on-measure-spaces-so-that-category-th. Although I can only understand some small part of them, I hope they can be interesting to you!
Thanks!
23 March, 2013 at 5:05 am
Marek
Dear Prof. Tao,
Excellent post, thank you for sharing! I have a related question, and I would be very grateful if you or someone else could provide me an answer.
As is well-known, the total variation distance between (the laws of) two random variables X and Y defined on R is given by sup|E[g(X)]−E[g(Y)]|, where the supremum is taken over all g:R→[0,1] that are measurable. Here is my question: do we obtain the same definition if one considers the supremum over all g:R→[0,1] that are continuous? Or over all g:R→[0,1] that are differentiable?
Thanks a lot in advance!
23 March, 2013 at 7:11 am
Terence Tao
Yes, basically because test functions are dense in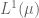 for any Borel probability measure on the real line (note that all Borel probability measures on R are Radon measures), thanks to basic tools such as the Stone-Weierstrass theorem, Lusin’s theorem, the Tietze extension theorem, and Urysohn’s lemma (as discussed in this previous blog post). Applying this general fact to
for any Borel probability measure on the real line (note that all Borel probability measures on R are Radon measures), thanks to basic tools such as the Stone-Weierstrass theorem, Lusin’s theorem, the Tietze extension theorem, and Urysohn’s lemma (as discussed in this previous blog post). Applying this general fact to  , the Borel probability measure formed by the average of the two laws, and using the Radon-Nikodym theorem to write
, the Borel probability measure formed by the average of the two laws, and using the Radon-Nikodym theorem to write 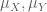 as bounded multiples of
as bounded multiples of  , we obtain the desired equivalence.
, we obtain the desired equivalence.
23 March, 2013 at 7:56 am
Marek
Thank you very much for the prompt reply! It is very clear in my mind now. Best, Marek
11 July, 2013 at 11:53 am
Probability and Statistics Books Online | Download free ebook
[…] A review of probability theory by Terence Tao, 2010 […]
16 September, 2013 at 7:12 am
Free Mathematics eBooks Online : Probability and Statistics | Top Free Books
[…] A review of probability theory by Terence Tao, 2010 […]
16 November, 2013 at 10:12 pm
Qualitative probability theory, types, and the group chunk and group configuration theorems | What's new
[…] classical foundations of probability theory (discussed for instance in this previous blog post) is founded on the notion of a probability space – a space (the sample space) equipped with […]
16 November, 2013 at 10:12 pm
Qualitative probability theory, types, and the group chunk and group configuration theorems | What's new
[…] classical foundations of probability theory (discussed for instance in this previous blog post) is founded on the notion of a probability space – a space (the sample space) equipped with […]
10 June, 2014 at 6:23 pm
Ehsan
Dear Prof. Tao,
Thank you for sharing your notes!
My question is about the probabilistic way of thinking. I understand that the cardinality of an event is not probabilistic notion because it is not preserved under the extension of the probability space.
Can rank and eigenvalues be probabilistic notions? If we consider the space of n-by-n matrices and extend it to the space of n+1-by-n+1 matrices, the the rank and eigenvalues may change as well.
I think I am missing something here.
Thanks!
10 June, 2014 at 9:13 pm
Terence Tao
The space of n by n matrices is not a probability space (and conversely, most probability spaces are not spaces of matrices), so I don’t see how your scenario would connect with probability theory.
Of course, if one had a matrix-valued random variable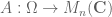 (i.e. a random matrix), one could compute its rank and eigenvalues, giving a random natural number and a random (multi-)set of points (i.e. a point process) respectively. These would all be probabilistic notions, but in all cases one would be extending the probabilistic domain
(i.e. a random matrix), one could compute its rank and eigenvalues, giving a random natural number and a random (multi-)set of points (i.e. a point process) respectively. These would all be probabilistic notions, but in all cases one would be extending the probabilistic domain  rather than the matrix space
rather than the matrix space 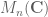 when performing probabilistic extensions.
when performing probabilistic extensions.
11 June, 2014 at 3:05 pm
Ehsan
Dear Prof. Tao,
Thank you for the answer. As you mentioned, I missed the fact that the probabilistic domain $\Omega$ is extended rather than the space of matrices.
16 June, 2014 at 7:47 pm
CRQ
Dear Prof Tao,
quick notation question: in definition 1, you say ”for some independent of
independent of  and all
and all 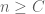 ”. Do you mean instead that there exists
”. Do you mean instead that there exists 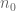 such that this holds ”for some
such that this holds ”for some  independent of
independent of  and all
and all 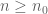 ? Thank you!
? Thank you!
17 June, 2014 at 6:26 am
Terence Tao
As long as there are no parameters in play besides , this is equivalent to the definition presented, since one could always raise either
, this is equivalent to the definition presented, since one could always raise either  or
or 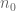 to be equal to each other. Once there are parameters, though, one has to be more careful. For instance if there are two parameters
to be equal to each other. Once there are parameters, though, one has to be more careful. For instance if there are two parameters 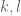 and one is asserting that
and one is asserting that 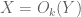 , then the conventions I use are that this means that
, then the conventions I use are that this means that  for all
for all 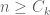 , where
, where 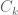 depends only on
depends only on  but not on
but not on 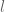 or
or  . With the definition involving
. With the definition involving 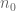 , it can be ambiguous as to whether
, it can be ambiguous as to whether 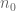 is allowed to depend on
is allowed to depend on 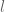 or not.
or not.
17 June, 2014 at 10:03 pm
nomen
I have been trying to define/explore “conditional random variables” for a while. In particular, I find that “sampling notation”, and what appears to be an adjunction in the algebra of random variables, makes them very natural. For example, consider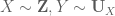 . It is very natural to treat
. It is very natural to treat  as being conditional on
as being conditional on  , since
, since  is uniformly distributed on
is uniformly distributed on 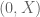 .
.
However, when I have tried to find out about this idea (mostly on math.stackexchange.com and mathoverflow.net), people have been dismissive. Actually, somebody on mathoverflow.net was supportive and suggested that I look into disintegrations.
Can you comment on the feasibility of defining such objects? Are they compatible with distintegrations, as you have used them?
17 June, 2014 at 10:09 pm
nomen
Sorry for the self-reply. I just wanted to clarify my motivation.
I often see that used as shorthand for
used as shorthand for
This “sample and bind” shorthand seems completely straight-forward to me, since we can “always” recover the distribution of Y from the joint distribution of (X,Y) by marginalizing X out. Are marginalizing and conditioning adjoints? It seems that the notation witnesses triple-ability, if they are adjoint at all.
This is effectively what I asked on mathoverflow.
22 June, 2014 at 11:15 am
Felix V.
Dear Prof. Tao,
thank you very much for this nice post and your book on Random Matrices.
as I noted in this (http://math.stackexchange.com/questions/842989/the-completeness-assumption-in-prokhorovs-theorem/843397#843397) stackexchange post, Exercise 23 seems to have mild problems.
You only assume that is
is  -compact, not necessarily complete.
-compact, not necessarily complete.
In that case, part (iv) of that exercise fails. Take e.g. . Then there are no nontrivial continuous functions with compact support, so that one of the conditions is vacuous.
. Then there are no nontrivial continuous functions with compact support, so that one of the conditions is vacuous.
I am also not sure that part (i) is really true in that setting. The proofs that I found all use the completeness of to show that certain sets (namely of the form
to show that certain sets (namely of the form 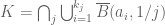 are compact, as they are closed and totally bounded).
are compact, as they are closed and totally bounded).
Sadly, I did not manage to produce a counterexample up to now.
Best regards,
Felix V.
22 June, 2014 at 1:11 pm
Terence Tao
Oops, you’re right; I had intended to assume that the metric space is both sigma compact and locally compact, but I think I thought that the latter hypotheses was implied by the former one for metric spaces, but as you point out, the example of the rationals shows that this is not the case. I’ve modified the text accordingly.
24 June, 2014 at 5:14 am
Felix V.
Thanks for the answer.
In my post above I was actually referring to part (ii) of the exercise, not part (i), sorry about that.
Do you know if this part (ii) is correct without the completeness assumption? Wikipedia (http://en.wikipedia.org/wiki/Prokhorov%27s_theorem , part 1 of “Statement of the theorem”) also only assumes that the metric space is separable, but they give neither a proof, nor a source.
24 June, 2014 at 7:42 am
Xiteng Liu
Congratulations Terry for The Breakthrough Award! You deserve it for your endeavor and enthusiasm in math.
27 June, 2014 at 3:00 am
Alon Gonen
Dear professor Terrence Tao,
How do you derive equation 1.24 using dominated converge?
Thanks
27 June, 2014 at 12:29 pm
Terence Tao
15 July, 2014 at 4:22 am
Real analysis relative to a finite measure space | What's new
[…] 1 In my previous post on the foundations of probability theory, I emphasised the freedom to extend the sample space to a larger sample space whenever one wished […]
11 August, 2014 at 7:40 am
254A, Notes 0: A review of probability theory | Mathemania
[…] 254A, Notes 0: A review of probability theory. […]
4 March, 2015 at 12:57 pm
Aryeh
Dear Prof. Tao, I don’t see how Poisson variables are subgaussian. In particular, the Laplace transform of the Poisson distribution is not upper-bounded by $e^{c t^2}$. Best, -Aryeh
[Oops, you’re right – corrected, thanks -T.]
29 September, 2015 at 9:54 pm
275A, Notes 0: Foundations of probability theory | What's new
[…] the classical measure-theoretic foundations of probability. (I wrote on these foundations also in this previous blog post, but in that post I already assumed that the reader was familiar with measure theory and basic […]
3 October, 2015 at 2:58 pm
275A, Notes 1: Integration and expectation | What's new
[…] Remark 2 There is one minor exception to this general rule if we do not impose the additional requirement that the factor map is surjective. Namely, for non-surjective , it can become possible that two events are unequal in the original sample space model, but become equal in the extension (and similarly for random variables), although the converse never happens (events that are equal in the original sample space always remain equal in the extension). For instance, let be the discrete probability space with and , and let be the discrete probability space with , and non-surjective factor map defined by . Then the event modeled by in is distinct from the empty event when viewed in , but becomes equal to that event when viewed in . Thus we see that extending the sample space by a non-surjective factor map can identify previously distinct events together (though of course, being probability preserving, this can only happen if those two events were already almost surely equal anyway). This turns out to be fairly harmless though; while it is nice to know if two given events are equal, or if they differ by a non-null event, it is almost never useful to know that two events are unequal if they are already almost surely equal. Alternatively, one can add the additional requirement of surjectivity in the definition of an extension, which is also a fairly harmless constraint to impose (this is what I chose to do in this previous set of notes). […]
6 October, 2015 at 9:40 am
Ben Golub
As a complement to Durrett’s book, I always found Amir Dembo’s notes on probability to be useful for a course of this type… their main virtue is that they are very systematic and (perhaps obsessively!) organized. http://statweb.stanford.edu/~adembo/stat-310a/lnotes.pdf
24 May, 2016 at 7:40 am
Robert
Thanks for the post. In relating to Terry’s definition of random matrices, does anybody know what is the best way to define a random matrix when its shape is also random variable? For instance, if A is random matrix such that A: Omega -> {space of matrices with m rows}. Thus A maps to the space of matrices with m rows, but the number of columns is itself a random variable. Is there a common way to construct of such a random matrix?
13 July, 2017 at 4:39 pm
Making Probability Mathematical | Infinite Series
[…] 254A, Notes 0: A review of probability theory Kolmogorov – Foundations of the Theory of Probability Ian Hacking – The Emergence of Probability […]
22 November, 2017 at 8:04 am
Mateo Wirth
I am having trouble with the definition of a disintegration given above. In particular, without the condition that for any measurable subset S of R, letting E be the event that Y is in S, we have
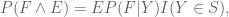
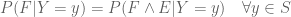 .
.
I can’t seem to conclude that
22 November, 2017 at 8:13 am
Mateo Wirth
Nevermind I see how it works now. Sorry!
12 February, 2019 at 6:33 am
The probability space as a fiction | Hydrobates
[…] search starting from this suspicion let me to an enlightening blog post of Terry Tao called ‘Notes 0: A review of probability theory‘. There he reviews ‘foundational aspects of probability theory’. Fairly early in […]
23 February, 2019 at 1:12 pm
What's the meaning of "random" in Mathematics? | Page 2 | Physics Forums
[…] measure space; we will return to this point when we discuss free probability later in this course. https://terrytao.wordpress.com/2010/01/01/254a-notes-0-a-review-of-probability-theory/ so for starting out: why not focus on probabilistic concepts as opposed to representation in […]
7 August, 2019 at 8:33 am
Making Probability Mathematical | Infinite Series - دکتر تیز
[…] 254A, Notes 0: A review of probability theory Kolmogorov – Foundations of the Theory of Probability Ian Hacking – The Emergence of Probability […]
12 November, 2019 at 6:47 pm
254A, Notes 9 – second moment and entropy methods | What's new
[…] In these notes we presume familiarity with the basic concepts of probability theory, such as random variables (which could take values in the reals, vectors, or other measurable spaces), probability, and expectation. Much of this theory is in turn based on measure theory, which we will also presume familiarity with. See for instance this previous set of lecture notes for a brief review. […]
14 December, 2019 at 12:58 pm
Is there a category consisting of probability spaces as objects and measurable functions as morphisms? – Lofgren's financial decisions
[…] this post, Terance Tao writes ”probability theory is only ‘allowed’ to study concepts and […]
7 July, 2020 at 7:05 pm
Server Bug Fix: Categorification of probability theory: what does a “probability sheaf” tell us (if anything) about probability theory? - TECHPRPR
[…] If you’re interested in this field, I think you will want to read these references (plus the blog post by Tao that Simpson cites), and you may need to give it time before super compelling applications […]
12 January, 2021 at 2:44 am
Anonymous
Dear Prof. Tao,
I am an undergraduate student majoring in mathematics, and I really enjoyed the way you explained the “probabilistic way of thinking” and ideas of conditioning on events or extending the sample space in a way far better than most introductory texts that I’ve read. (Although most of this article went over my head). I would be really grateful if you could suggest some references/ lecture notes written in a similar style, which are more suited to an undergraduate looking to learn probability theory.
Thank you.
11 October, 2021 at 9:19 am
254A, Supplement 4: Probabilistic models and heuristics for the primes (optional) | What's new
[…] material in this set of notes presumes some prior exposure to probability theory. See for instance this previous post for a quick review of the relevant […]