A recurring theme in mathematics is that of duality: a mathematical object can either be described internally (or in physical space, or locally), by describing what
physically consists of (or what kind of maps exist into
), or externally (or in frequency space, or globally), by describing what
globally interacts or resonates with (or what kind of maps exist out of
). These two fundamentally opposed perspectives on the object
are often dual to each other in various ways: performing an operation on
may transform it one way in physical space, but in a dual way in frequency space, with the frequency space description often being a “inversion” of the physical space description. In several important cases, one is fortunate enough to have some sort of fundamental theorem connecting the internal and external perspectives. Here are some (closely inter-related) examples of this perspective:
- Vector space duality A vector space
over a field
can be described either by the set of vectors inside
, or dually by the set of linear functionals
from
to the field
(or equivalently, the set of vectors inside the dual space
). (If one is working in the category of topological vector spaces, one would work instead with continuous linear functionals; and so forth.) A fundamental connection between the two is given by the Hahn-Banach theorem (and its relatives).
- Vector subspace duality In a similar spirit, a subspace
of
can be described either by listing a basis or a spanning set, or dually by a list of linear functionals that cut out that subspace (i.e. a spanning set for the orthogonal complement
. Again, the Hahn-Banach theorem provides a fundamental connection between the two perspectives.
- Convex duality More generally, a (closed, bounded) convex body
in a vector space
can be described either by listing a set of (extreme) points whose convex hull is
, or else by listing a set of (irreducible) linear inequalities that cut out
. The fundamental connection between the two is given by the Farkas lemma.
- Ideal-variety duality In a slightly different direction, an algebraic variety
in an affine space
can be viewed either “in physical space” or “internally” as a collection of points in
, or else “in frequency space” or “externally” as a collection of polynomials on
whose simultaneous zero locus cuts out
. The fundamental connection between the two perspectives is given by the nullstellensatz, which then leads to many of the basic fundamental theorems in classical algebraic geometry.
- Hilbert space duality An element
in a Hilbert space
can either be thought of in physical space as a vector in that space, or in momentum space as a covector
on that space. The fundamental connection between the two is given by the Riesz representation theorem for Hilbert spaces.
- Semantic-syntactic duality Much more generally still, a mathematical theory can either be described internally or syntactically via its axioms and theorems, or externally or semantically via its models. The fundamental connection between the two perspectives is given by the Gödel completeness theorem.
- Intrinsic-extrinsic duality A (Riemannian) manifold
can either be viewed intrinsically (using only concepts that do not require an ambient space, such as the Levi-Civita connection), or extrinsically, for instance as the level set of some defining function in an ambient space. Some important connections between the two perspectives includes the Nash embedding theorem and the theorema egregium.
- Group duality A group
can be described either via presentations (lists of generators, together with relations between them) or representations (realisations of that group in some more concrete group of transformations). A fundamental connection between the two is Cayley’s theorem. Unfortunately, in general it is difficult to build upon this connection (except in special cases, such as the abelian case), and one cannot always pass effortlessly from one perspective to the other.
- Pontryagin group duality A (locally compact Hausdorff) abelian group
can be described either by listing its elements
, or by listing the characters
(i.e. continuous homomorphisms from
to the unit circle, or equivalently elements of
). The connection between the two is the focus of abstract harmonic analysis.
- Pontryagin subgroup duality A subgroup
of a locally compact abelian group
can be described either by generators in
, or generators in the orthogonal complement
. One of the fundamental connections between the two is the Poisson summation formula.
- Fourier duality A (sufficiently nice) function
on a locally compact abelian group
(equipped with a Haar measure
) can either be described in physical space (by its values
at each element
of
) or in frequency space (by the values
at elements
of the Pontryagin dual
). The fundamental connection between the two is the Fourier inversion formula.
- The uncertainty principle The behaviour of a function
at physical scales above (resp. below) a certain scale
is almost completely controlled by the behaviour of its Fourier transform
at frequency scales below (resp. above) the dual scale
and vice versa, thanks to various mathematical manifestations of the uncertainty principle. (The Poisson summation formula can also be viewed as a variant of this principle, using subgroups instead of scales.)
- Stone/Gelfand duality A (locally compact Hausdorff) topological space
can be viewed in physical space (as a collection of points), or dually, via the
algebra
of continuous complex-valued functions on that space, or (in the case when
is compact and totally disconnected) via the boolean algebra of clopen sets (or equivalently, the idempotents of
). The fundamental connection between the two is given by the Stone representation theorem or the (commutative) Gelfand-Naimark theorem.
I have discussed a fair number of these examples in previous blog posts (indeed, most of the links above are to my own blog). In this post, I would like to discuss the uncertainty principle, that describes the dual relationship between physical space and frequency space. There are various concrete formalisations of this principle, most famously the Heisenberg uncertainty principle and the Hardy uncertainty principle – but in many situations, it is the heuristic formulation of the principle that is more useful and insightful than any particular rigorous theorem that attempts to capture that principle. Unfortunately, it is a bit tricky to formulate this heuristic in a succinct way that covers all the various applications of that principle; the Heisenberg inequality is a good start, but it only captures a portion of what the principle tells us. Consider for instance the following (deliberately vague) statements, each of which can be viewed (heuristically, at least) as a manifestation of the uncertainty principle:
- A function which is band-limited (restricted to low frequencies) is featureless and smooth at fine scales, but can be oscillatory (i.e. containing plenty of cancellation) at coarse scales. Conversely, a function which is smooth at fine scales will be almost entirely restricted to low frequencies.
- A function which is restricted to high frequencies is oscillatory at fine scales, but is negligible at coarse scales. Conversely, a function which is oscillatory at fine scales will be almost entirely restricted to high frequencies.
- Projecting a function to low frequencies corresponds to averaging out (or spreading out) that function at fine scales, leaving only the coarse scale behaviour.
- Projecting a frequency to high frequencies corresponds to removing the averaged coarse scale behaviour, leaving only the fine scale oscillation.
- The number of degrees of freedom of a function is bounded by the product of its spatial uncertainty and its frequency uncertainty (or more generally, by the volume of the phase space uncertainty). In particular, there are not enough degrees of freedom for a non-trivial function to be simulatenously localised to both very fine scales and very low frequencies.
- To control the coarse scale (or global) averaged behaviour of a function, one essentially only needs to know the low frequency components of the function (and vice versa).
- To control the fine scale (or local) oscillation of a function, one only needs to know the high frequency components of the function (and vice versa).
- Localising a function to a region of physical space will cause its Fourier transform (or inverse Fourier transform) to resemble a plane wave on every dual region of frequency space.
- Averaging a function along certain spatial directions or at certain scales will cause the Fourier transform to become localised to the dual directions and scales. The smoother the averaging, the sharper the localisation.
- The smoother a function is, the more rapidly decreasing its Fourier transform (or inverse Fourier transform) is (and vice versa).
- If a function is smooth or almost constant in certain directions or at certain scales, then its Fourier transform (or inverse Fourier transform) will decay away from the dual directions or beyond the dual scales.
- If a function has a singularity spanning certain directions or certain scales, then its Fourier transform (or inverse Fourier transform) will decay slowly along the dual directions or within the dual scales.
- Localisation operations in position approximately commute with localisation operations in frequency so long as the product of the spatial uncertainty and the frequency uncertainty is significantly larger than one.
- In the high frequency (or large scale) limit, position and frequency asymptotically behave like a pair of classical observables, and partial differential equations asymptotically behave like classical ordinary differential equations. At lower frequencies (or finer scales), the former becomes a “quantum mechanical perturbation” of the latter, with the strength of the quantum effects increasing as one moves to increasingly lower frequencies and finer spatial scales.
- Etc., etc.
- Almost all of the above statements generalise to other locally compact abelian groups than
or
, in which the concept of a direction or scale is replaced by that of a subgroup or an approximate subgroup. (In particular, as we will see below, the Poisson summation formula can be viewed as another manifestation of the uncertainty principle.)
I think of all of the above (closely related) assertions as being instances of “the uncertainty principle”, but it seems difficult to combine them all into a single unified assertion, even at the heuristic level; they seem to be better arranged as a cloud of tightly interconnected assertions, each of which is reinforced by several of the others. The famous inequality is at the centre of this cloud, but is by no means the only aspect of it.
The uncertainty principle (as interpreted in the above broad sense) is one of the most fundamental principles in harmonic analysis (and more specifically, to the subfield of time-frequency analysis), second only to the Fourier inversion formula (and more generally, Plancherel’s theorem) in importance; understanding this principle is a key piece of intuition in the subject that one has to internalise before one can really get to grips with this subject (and also with closely related subjects, such as semi-classical analysis and microlocal analysis). Like many fundamental results in mathematics, the principle is not actually that difficult to understand, once one sees how it works; and when one needs to use it rigorously, it is usually not too difficult to improvise a suitable formalisation of the principle for the occasion. But, given how vague this principle is, it is difficult to present this principle in a traditional “theorem-proof-remark” manner. Even in the more informal format of a blog post, I was surprised by how challenging it was to describe my own understanding of this piece of mathematics in a linear fashion, despite (or perhaps because of) it being one of the most central and basic conceptual tools in my own personal mathematical toolbox. In the end, I chose to give below a cloud of interrelated discussions about this principle rather than a linear development of the theory, as this seemed to more closely align with the nature of this principle.
— 1. An informal foundation for the uncertainty principle —
Many of the manifestations of the uncertainty principle can be heuristically derived from the following informal heuristic:
Heuristic 1 (Phase heuristic) If the phase
of a complex exponential
fluctuates by less than
for
in some nice domain
(e.g. a convex set, or more generally an approximate subgroup), then the phase
behaves as if it were constant on
. If instead the phase fluctuates by much more than
, then
should oscillate and exhibit significant cancellation. The more the phase fluctuates, the more oscillation and cancellation becomes present.
For instance, according to this heuristic, on an interval in the real line, the linear phase
at a given frequency
behaves like a constant when
, but oscillates significantly when
. This is visually plausible if one graphs the real and imaginary parts
,
. For now, we will take this principle as axiomatic, without further justification, and without further elaboration as to what vague terms such as “behaves as if” or
mean.
We remark in passing that, the above heuristic can also be viewed as the informal foundation for the principle of stationary phase. This is not coincidental, but will not be the focus of the discussion here.
Let’s give a few examples to illustrate how this heuristic informally implies some versions of the uncertainty principle. Suppose for instance that a function is supported in an interval
. Now consider the Fourier transform
(Other normalisations of the Fourier transform are possible, but this does not significantly affect the discussion here.) We assume that the function is nice enough (e.g. absolutely integrable will certainly suffice) that one can define the Fourier transform without difficulty.
If , then the phase
fluctuates by less than
on the domain
, and so the phase here is essentially constant by the above heuristic; in particular, we expect the Fourier transform
to not vary much in this interval. More generally, if we consider frequencies
in an interval
for a fixed
, then on separating
as
, the latter phase
is essentially constant by the above heuristic, and so we expect
to not vary much in this interval either. Thus
is close to constant at scales much finer than
, just as the uncertainty principle predicts.
A similar heuristic calculation using the Fourier inversion formula
shows that if the Fourier transform is restricted to an interval
, then the function
should behave roughly like a constant at scales
. A bit more generally, if the Fourier transform is restricted to an interval
, then by separating
as
and discarding the last phase when
, we see that the function
behaves like a constant multiple of the plane wave
on each interval
(but it could be a different constant multiple on each such interval).
The same type of heuristic computation can be carried through in higher dimensions. For instance, if a function has Fourier transform supported in some symmetric convex body
, then one expects
itself to behave like a constant on any translate
of a small multiple
of the polar body
of .
An important special case where the above heuristics are in fact exactly rigorous is when one does not work with approximate subgroups such as intervals or convex bodies
, but rather with subgroups
of the ambient (locally compact abelian) group
that is serving as physical space. Here, of course, we need the general Fourier transform
where is a Haar measure on the locally compact abelian group
, where
is a continuous homomorphism from
to
(and is thus an element of the Pontryagin dual group
), with Fourier transform given by the inversion formula
wheere is the dual Haar measure on
(see e.g. my lecture notes for further discussion of this general theory). If
is supported on a subgroup
of
(this may require
to be a measure rather than a function, if
is a measure zero subgroup of
), we conclude (rigorously!) that
is constant along cosets of the orthogonal complement
For instance, a measure on
that is supported on
will have a Fourier transform
that is constant along the
direction, as
is its own orthogonal complement. This is a basic component of the Poisson summation formula. (The situation becomes more complicated if
is merely a distribution rather than a measure, but we will not discuss this technical issue here.)
Remark 1 Of course, in Euclidean domains such as
or
, basic sets such as the intervals
are not actual subgroups, but are only approximate subgroups (roughly speaking, this means that they are closed under addition a “reasonable fraction of the time”; for a precise definition, see my book with Van Vu). However, there are dyadic models of Euclidean domains, such as the field
of formal Laurent series in a variable
over a finite field
, in which the analogues of such intervals are in fact actual subgroups, which allows for a very precise and rigorous formalisation of many of the heuristics given here in that setting. See for instance these lecture notes of mine for more discussion.
One can view an interval such as as being an approximate orthogonal complement to the interval
, and more generally the polar body
as an approximate orthogonal complement to
. Conversely, the uncertainty principle
when specialised to subgroups
of a finite abelian group
becomes the equality
and when specialised to subspaces of a Euclidean space
becomes
We saw above that a function that was restricted to a region
would necessarily have a Fourier transform
that was essentially constant on translates of (small multiples of) the dual region
. This implication can be partially reversed. For instance, suppose that
behaved like a constant at all scales
. Then if one inspects the Fourier inversion formula
we note that if , then
oscillates at scales
by the above heuristic, and so
should be negligible when
.
The above heuristic computations can be made rigorous in a number of ways. One basic method is to exploit the fundamental fact that the Fourier transform intertwines multiplication and convolution, thus
and
and similarly for the inverse Fourier transform. (Here, the convolution is with respect to either the Haar measure
on the physical space
, or the Haar measure
on the frequency space
, as indicated by context.) For instance, if a function
has Fourier transform supported on
, then we have
where and
is a smooth and compactly supported (or rapidly decreasing) cutoff function that equals
on the interval
. (There is a lot of freedom here in what cutoff function to pick, but in practice, “all bump functions are usually equivalent”; unless one is optimising constants, needs a very specific and delicate cancellation, or if one really, really needs a explicit formula, one usually does not have to think too hard regarding what specific cutoff to use, though smooth and well localised cutoffs often tend to be superior to rough or slowly decaying cutoffs.)
Inverting the Fourier transform, we obtain the reproducing formula
where is the inverse Fourier transform of
. One can compute that
If one chose to be smooth and compactly supported (or at the very least, a Schwartz function),
will be in the Schwartz class. As such, (1) can be viewed as an assertion that the value of the band-limited function
at any given point
is essentially an average of its values at nearby points
for
. This formula can already be used to give many rigorous instantiations of the uncertainty principle; see for instance these lecture notes of mine for further discussion.
Another basic method to formalise the above heuristics, particularly with regard to “oscillation causes cancellation”, is to use integration by parts; this is discussed at this Tricki article.
— 2. Projections —
The restriction of a function
to an interval
is just the orthogonal projection (in the Hilbert space
) of
to the space of functions that are spatially supported in
. Taking Fourier transforms (which, by Plancherel’s theorem, preserves the Hilbert space
), we see that the Fourier restriction
of
, defined as
is the orthogonal projection of to those functions with Fourier support in
. As discussed above, such functions are (heuristically) those functions which are essentially constant at scales
. As such, these projection operators should behave like averaging operators at this scale. This turns out not to be that accurate of a heuristic if one uses the sharp cutoffs
(though this does work perfectly in the dyadic model setting), but if one replaces the sharp cutoffs by smoother ones, then this heuristic can be justified by using convolutions as in the previous section; this leads to Littlewood-Paley theory, a cornerstone of the harmonic analysis of function spaces such as Sobolev spaces, and which are particularly important in partial differential equations; see for instance the first appendix of my PDE book for further discussion.
One can view the restriction operator as the spectral projection of the position operator
to the interval
; in a similar vein, one can view
as a spectral projection of the differentiation operator
.
As before, one can work with other sets than intervals here. For instance, restricting a function to a subgroup
causes the Fourier transform
to be averaged along the dual group
. In particular, restricting a function
to the integers (and renormalising it to become the measure
) causes the Fourier transform
to become summed over the dual group
to become the function
. In particular, the zero Fourier coefficient of
is
, leading to the Poisson summation formula
More generally, one has
for any , which can be viewed as a one-parameter family of identities interpolating between the inversion formula
on one hand, and the forward Fourier transform formula
on the other.
The duality between the position variable
and the frequency variable
(or equivalently, between the position operator
and the differentiation operator
) can be generalised to contexts in which the two dual variables haved a different “physical” interpretation than position and frequency. One basic example of this is the duality
between a time variable
and an energy variable
in quantum mechanics. Consider a time-dependent Schrödinger equation
for some Hermitian (and time-independent) spatial operator on some arbitrary domain (which does not need to be a Euclidean space
, or even a group), where we have normalised away for now the role of Planck’s constant
. If the underlying spatial space
has an orthonormal basis of eigenvector solutions to the time-independent Schrödinger equation
then the solution to (2) is formally given by the formula
We thus see that the coefficients (or more precisely, the eigenvectors
) can be viewed as the Fourier coefficients of
in time, with the energies
playing the role of the frequency vector. Taking traces, one (formally) sees a similar Fourier relationship between the trace function
and the spectrum
:
As a consequence, the heuristics of the uncertainty principle carry through here. Just as the behaviour of a function at scales
largely controls the spectral behaviour of
at scales
, one can use the evolution operator
of the Schrödinger equation up to times
to understand the spectrum
of
at scales
. For instance, from (3) we (formally) see that
for any test function and any energy level
. Roughly speaking, this formula tells us that the number of eigenvalues in an interval of size
can be more or less controlled by the Schrödinger operators up to time
.
A similar analysis also holds for the solution operator
for the wave equation
on an arbitrary spatial Riemannian manifold (which we will take to be compact in order to have discrete spectrum). If we write
for the eigenvalues of
(so the Laplace-Beltrami operator
has eigenvalues
), then a similar analysis to the above shows that knowledge of the solution to the wave equation up to time
gives (at least in principle) knowledge of the spectrum averaged to at the scale
or above.
From the finite speed of propagation property of the wave equation (which has been normalised so that the speed of light is equal to
), one only needs to know the geometry of the manifold
up to distance scales
in order to understand the wave operator up to times
. In particular, if
is less than the injectivity radius of
, then the topology and global geometry of
is largely irrelevant, and the manifold more or less behaves like (a suitably normalised version of) Euclidean space. As a consequence, one can borrow Euclidean space techniques (such as the spatial Fourier transform) to control the spectrum at coarse scales
, leading in particular to the Weyl law for the distribution of eigenvalues on this manifold; see for instance this book of Sogge for a rigorous discussion. It is a significant challenge to go significantly below this scale and understand the finer structure of the spectrum; by the uncertainty principle, this task is largely equivalent to that of understanding the wave equation on long time scales
, and the global geometry of the manifold
(and in particular, the dynamical properties of the geodesic flow) must then inevitably play a more dominant role.
Another important uncertainty principle duality relationship is that between the (imaginary parts of the) zeroes of the Riemann zeta function
and the logarithms
of the primes. Starting from the fundamental Euler product formula
and using rigorous versions of the heuristic factorisation
one can soon derive explicit formulae connecting zeroes and primes, such as
(see e.g. this blog post of mine for more discussion). Using such formulae, one can relate the zeroes of the zeta function in the strip with the distribution of the log-primes at scales
. For instance, knowing that there are no zeroes on the line segment
is basically equivalent to a partial prime number theorem
; letting
, we see that the full prime number theorem is equivalent to the absence of zeroes on the entire line
. More generally, there is a fairly well-understood dictionary between the distribution of zeroes and the distribution of primes, which is explored in just about any advanced text in analytic number theory.
— 3. Phase space and the semi-classical limit —
The above heuristic description of Fourier projections such as suggest that a Fourier projection
will approximately commute with a spatial projection
whenever
,
are intervals that obey the Heisenberg inequality
. Again, this heuristic is not quite accurate if one uses sharp cutoffs (except in the dyadic model), but becomes quite valid if one uses smooth cutoffs. As such, one can morally talk about phase space projections
to rectangles
in phase space, so long as these rectangles are large enough not to be in violation of the uncertainty principle.
Heuristically, is an orthogonal projection to the space of functions that are localised to
in physical space and to
in frequency space. (This is morally a vector space, but unfortunately this is not rigorous due to the inability to perfectly localise in both physical space and frequency space simultaneously, thanks to the Hardy uncertainty principle.) One can approximately compute the dimension of this not-quite-vector-space by computing the trace of the projection. Recalling that the trace of an integral operator
is given by
, a short computation reveals that the trace of
is
Thus we conclude that the phase space region contains approximately
degrees of freedom in it, which can be viewed as a “macroscopic” version of the uncertainty principle.
More generally, the number of degrees of freedom contained in a large region of phase space is proportional to its area. Among other things, this can be used to justify the Weyl law for the distribution of eigenvalues of various operators. For instance, if
is the Schrödinger operator
where is a small constant (which physically can be interpreted as Planck’s constant), and
is a confining potential (to ensure discreteness of the spectrum), then the spectral projection
, when spectrally projected to energy levels below a given threshold
, is morally like a phase space projection to the region
. As such, the number of eigenvalues of
less than
should roughly equal the area of
, particularly when
is small (so that
becomes large, and the uncertainty principle no longer dominates); note that if
is a confining potential (such as the harmonic potential
) then
will have finite area. Such heuristics can be justified by the machinery of semi-classical analysis and the pseudo-differential calculus, which we will not detail here.
The correspondence principle in quantum mechanics asserts that in the limit , quantum mechanics asymptotically converges (in some suitable sense) to classical mechanics. There are several ways to make this precise. One can work in a dual formulation, using algebras of observables rather than dealing with physical states directly, in which case the point is that the non-commutative operator algebras of quantum observables converge in various operator topologies to the commutative operator algebras of classical observables in the limit
. This is the most common way that the correspondence principle is formulated; but one can also work directly using states. We illustrate this with the time-dependent Schrödinger equation
with a potential , where
is a fixed constant (representing mass) and
is a small constant, or equivalently
where is the position operator
and
is the momentum operator
(thus
). The classical counterpart to this equation is Newton’s second law
where and
; introducing the momentum
, one can rewrite Newton’s second law as Hamilton’s equations of motion
We now indicate (heuristically, at least) how (4) converges to (5) as . According to de Broglie’s law
, the momentum
should be proportional to the frequency
. Accordingly, consider a wave function
that at time
is concentrated near position
and momentum
, and thus near frequency
; heuristically one can view
as having the shape
where is some phase,
is some spatial scale (between
and
) and
is some amplitude function. Informally, we have
and
for
.
Before we analyse the equation (4), we first look at some simpler equations. First, we look at
where is a real scalar constant. Then the evolution of this equation is given by a simple phase rotation:
This phase rotation does not change the location or momentum
of the wave:
Next, we look at the transport equation
where is another constant This evolution is given by translation:
the position of this evolution moves at the constant speed of
, but the momentum is unchanged:
Combining the two, we see that an equation of the form
would also transport the position at a constant speed of
, without changing the momentum. Next, we consider the modulation equation
where is yet another constant. This equation is solved by the formula
this phase modulation does not change the position , but steadily increases the momentum
at a rate of
:
Finally, we combine all these equations together, looking at the combined equation
Heuristically at least, the position and momentum
of solutions to this equation should evolve according to the law
We remark that one can make the above quite rigorous by using the metaplectic representation.
This analysis was for constant, but as all statements here are instantaneous and first-order in time, it also applies for time-dependent
.
Now we return to the Schrödinger equation (4). If is localised in space close to
, then by Taylor expansion we may linearise the
component as
Similarly, if is localised in momentum close to
, then in frequency it is localised close to
, so that
, and so we have a Taylor expansion
These Taylor expansions become increasingly accurate in the limit , assuming suitable localisation in both space and momentum. Inserting these approximations and simplifying, one arrives at
where is the classical energy of the state. Using the heuristics (6) we are led to (5) as desired.
More generally, a Schrödinger equation
where is the momentum operator, and being vague about exactly what a function
of two non-commuting operators
means, can be (heuristically) approximately Taylor expanded as
and (6) leads us to the Hamilton equations of motion
It turns out that these heuristic computations can be made completely rigorous in the semi-classical limit , by using the machinery of pseudodifferential calculus, but we will not detail this here.

27 comments
Comments feed for this article
26 June, 2010 at 8:50 am
David
At the end of the discussion of zeta, should be
should be 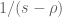 .
.
[Corrected, thanks. – T.]
26 June, 2010 at 8:52 am
David
Also, the in the exponential is surpuflous. Sorry for the double comment!
in the exponential is surpuflous. Sorry for the double comment!
[Corrected, thanks. – T.]
27 June, 2010 at 8:30 am
mfrasca
Hi Terry,
As you know, a duality principle holds true also in perturbation theory:
http://pra.aps.org/abstract/PRA/v58/i5/p3439_1
For a given problem with a small perturbation you can generally get a solution to the same one having the perturbation going to infinity.
Regards,
Marco
27 June, 2010 at 12:36 pm
Anonymous
There is a t missing in exponent of e^(-iE/h) in the equation just under “Then the evolution of this equation is given by a simple phase rotation: ”
[Corrected, thanks – T.]
28 June, 2010 at 11:31 am
Researcher
Great post! May I humbly suggest using a new tag “heuristics” for the posts like that? And anyway I’d be thrilled to see more posts on various heuristics in mathematics on your blog, with or without this tag :)
5 July, 2010 at 12:44 am
dmitin
http://en.wikipedia.org/wiki/Duality_(projective_geometry)
http://en.wikipedia.org/wiki/Duality_(projective_geometry)#Combinatorial_duality
11 August, 2010 at 8:30 pm
Anonymous
Professor Tao:
If we consider 1, 10 , 100, 1000… as basis we have a representation of integers in terms of these basis. I was wondering if there is a notion of harmonic analysis on integers apart from the fourier transform so that multiplication (which is just convolution with carry) could have a dual basis interpretation. Something like multiplication of polynomials using fft. It seems that the ordinary notion of Parseval’s theorem will not hold (or else product of sum of squares of digits of two numbers to be multiplied would be the sum of squares of the digits of the resulting integers which is untrue).
Thank you
18 August, 2010 at 5:57 am
Paul Shearer
Hi Terry,
Another beautiful example of duality comes from optimization theory, in the form of the Fenchel dual to a function. The Fenchel dual has the following physical interpretation, which nicely illustrates your theme of “dual intrinsic/extrinsic” descriptions of an object:
“A particle in a convex potential well can be pushed to any desired equilibrium point x by applying an appropriate force p. There is a bijective map relating x and p: the forward map is
can be pushed to any desired equilibrium point x by applying an appropriate force p. There is a bijective map relating x and p: the forward map is 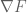 , while the inverse is
, while the inverse is  , where
, where  is the Fenchel dual to
is the Fenchel dual to  .”
.”
To be more formal, given a nice convex function , we can interpret it as a potential function that a particle rolls around in.
, we can interpret it as a potential function that a particle rolls around in.
Let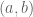 denote the inner product. Then the Fenchel dual to F is defined as
denote the inner product. Then the Fenchel dual to F is defined as
Let x be the point where the max is achieved. The point x can be interpreted as the equilibrium position of a particle in potential F when this particle is subjected to a constant “applied force” p. The function
can be interpreted as an effective potential induced by the applied force, and the Fenchel dual is implicitly finding x, the equilibrium point where this potential is minimized. With a little calc and algebra we find
(The negative is taken simply because the duality is cleaner if is convex rather than concave.) A little calculus shows that
is convex rather than concave.) A little calculus shows that
(*)
completing the justification of the physical interpretation at the top of this post.
The derivation of this fact is intriguing in itself; by applying the multivariate chain rule to differentiate
with respect to p, we find
The fact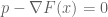 is known from above, and arises from the fact that the particle is at equilibrium; thus the only change in the effective potential arises from the change in the “applied potential” with respect to p alone, holding x constant.
is known from above, and arises from the fact that the particle is at equilibrium; thus the only change in the effective potential arises from the change in the “applied potential” with respect to p alone, holding x constant.
Another interesting fact: a nonrigorous but intuitively appealing derivation of the Fenchel dual, in particular the involutive property, is possible by the following geometric procedure:
1. draw a contour plot of some nice F.
2. draw a vector from 0 to a given equilibrium point x.
3. draw the applied force p as a vector pointing from point x to x + p.
Note that the two vectors drawn are now two sides of a parallelogram; the Fenchel dual is a function for which one can follow the exact same steps (1)-(3) again, but one uses the other two sides of the parallelogram and reverses the roles of p and x. After drawing this diagram, the involutive property of Fenchel duality becomes immediately obvious: taking the dual just means “flipping” the parallelogram over! :)
18 August, 2010 at 11:51 am
Paul Shearer
whoops! it’s supposed to be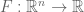 . sorry. Although I guess it’s still an interesting and nontrivial statement for n = 1. Just not as geometrically cool…
. sorry. Although I guess it’s still an interesting and nontrivial statement for n = 1. Just not as geometrically cool…
30 January, 2011 at 9:07 pm
Chen-bo Zhu
Hi Prof. Tao,
Before Remark 1, there is a typo: if H is a measure zero subgroup of H (which should be G). Also I think the statement that f^ is constant along cosets of the orthogonal complement may need a small revision since f can be a transversal derivative of a measure on H. [Corrected, thanks – T.]
Not sure if the following paragraph is appropriate as a follow-up to your blog, and so please feel free to remove this paragraph if it is not so.
There is a certain rigidity phenomenon of distributions with strong support properties, which may be considered as an another instance of the uncertainty principle:
Click to access rigidity-distribution.pdf
Regards, Chen-bo
30 March, 2011 at 9:33 am
Higher order Fourier analysis « What’s new
[…] was based primarily on my graduate course in the topic, though it also contains material from some additional posts related to linear and higher order Fourier analysis on the blog. It is available […]
4 August, 2011 at 6:53 pm
Localisation and compactness properties of the Navier-Stokes global regularity problem « What’s new
[…] the uncertainty principle (discussed in this post) suggests that . Finally, the linear term and nonlinear term have heuristic magnitudes about and […]
1 January, 2012 at 11:46 am
Montgomery’s uncertainty principle « What’s new
[…] One of the most fundamental principles in Fourier analysis is the uncertainty principle. It does not have a single canonical formulation, but one typical informal description of the principle is that if a function is restricted to a narrow region of physical space, then its Fourier transform must be necessarily “smeared out” over a broad region of frequency space. Some versions of the uncertainty principle are discussed in this previous blog post. […]
23 May, 2012 at 6:06 pm
Quora
What is an intuitive way of explaining how the “Fourier transform” works?…
Fourier transform is way of writing functions on a space as a superposition of symmetric functions. Depending on the space we are interested, there can be several symmetries associated to the function. For instance, the fourier transform on real line i…
17 July, 2015 at 4:01 pm
Lemme tell y’all about icosian calculus. | between bourbaki and me
[…] Sitting in a coffee shop, I wandered over to the wiki for the presentation of a group. A presentation is a natural idea in group theory, a compact way of describing a group by referring to a set of generators and relations between those generators. Fun fact, the presentation of a group is an example of an internal object description. This is part of a larger phenomenon in mathematics where we describe an object based on functions from similar objects into your object. For instance, the presentation is equivalent to a description of a map from a free group on a set of generators S into your group G. You essentially describe how to fold the free group up into your group! The internal description is in contrast with external, where you send maps out of your objects. In group theory, this is called representation theory. Tons more mind-blowing examples of internal-external definitions at Terry Tao’s blog. […]
10 December, 2015 at 12:13 pm
Decoupling and the Bourgain-Demeter-Guth proof of the Vinogradov main conjecture | What's new
[…] of Theorem 5.6 of Bourgain-Demeter-Guth, or my general discussion on the uncertainty principle in this previous blog post). This implies that , when restricted to , is essentially constant on “plates”, defined […]
14 March, 2017 at 9:17 am
On “external” definitions for computation | Windows On Theory
[…] to me to be an instance of moving to an external, as opposed to internal definition, in the sense described by Tao. (Please correct me if I’m wrong!) As Arkani-Hamed describes, a hugely important paper […]
5 January, 2020 at 11:58 pm
To lift and breathe – Tea and Skulls
[…] Internal descriptions stand in contrast with external descriptions. Can you guess what an external description might be like? If internal descriptions were maps into the group, then it would make sense if external descriptions were maps out of the group. Fortunately, things do make sense, and I’m not lying to you, so that’s exactly what external descriptions are. In group theory, the description of a group is called a representation. The study of representation is called representation. (If this internal-external business sounds cool to you, check out this dope post by Terry Tao: blog). […]
21 January, 2020 at 3:32 am
On generating functions in additive number theory, II: Lower-order terms and applications to PDEs | George Shakan
[…] By uncertainty principle heuristics, we expect , as defined in (1), to be constant on scales […]
5 March, 2020 at 7:14 pm
Daniel D
In (3) we have and then another expression that appears is
and then another expression that appears is  , as I understand just a position and momentum satisfy heisenberg uncertainty, time and energy also do
, as I understand just a position and momentum satisfy heisenberg uncertainty, time and energy also do  could
could  make sense?, thanks
make sense?, thanks
6 March, 2020 at 8:18 am
Terence Tao
Well, it’s rather than
rather than 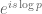 . So if one splits
. So if one splits  then the more accurate form of the uncertainty principle heuristic regarding the primes should be
then the more accurate form of the uncertainty principle heuristic regarding the primes should be  . Thus, for instance, if one wants to count the number of primes in an interval of the form
. Thus, for instance, if one wants to count the number of primes in an interval of the form ![[x, x+x/T]](https://s0.wp.com/latex.php?latex=%5Bx%2C+x%2Bx%2FT%5D&bg=ffffff&fg=545454&s=0&c=20201002) (so that
(so that  is confined to an interval of length
is confined to an interval of length  ), one should expect to need to control the Riemann zeta function
), one should expect to need to control the Riemann zeta function 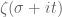 for heights
for heights 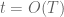 . And this is indeed the case if one looks at what the truncated Perron formula actually gives (see e.g., Proposition 12 of https://terrytao.wordpress.com/2014/12/09/254a-notes-2-complex-analytic-multiplicative-number-theory/ ).
. And this is indeed the case if one looks at what the truncated Perron formula actually gives (see e.g., Proposition 12 of https://terrytao.wordpress.com/2014/12/09/254a-notes-2-complex-analytic-multiplicative-number-theory/ ).
2 July, 2020 at 7:16 pm
trucupey
Hi, professor Tao, maybe I am not understanding well but in the example 14 of what you called heuristically statements, shouldn’t it say “In the low frequency (or large scale) limit, position and frequency asymptotically behave like a pair of classical observables … ” instead of “In the high frequency (or large scale) limit, position and frequency asymptotically behave like a pair of classical observables …” ?
7 July, 2020 at 5:31 pm
Terence Tao
To achieve the semiclassical limit one has to make the product much larger than Planck’s constant
much larger than Planck’s constant 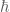 . There are two ways to do this: either go to high frequencies (so that
. There are two ways to do this: either go to high frequencies (so that  becomes large) or large scales (so that
becomes large) or large scales (so that 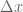 becomes large).
becomes large).
30 October, 2021 at 12:39 am
[scala] 프로그래밍에서 "대수"는 무엇을 의미합니까? - 리뷰나라
[…] 이중 공간 을 보는 이유 는 일반적으로 그 공간에서 생각하기가 더 쉽기 때문입니다. 예를 들어, 법선 벡터에 대해 법선 평면보다 생각하기가 더 쉬운 경우가 있지만 벡터로 평면 (하이 평면 포함)을 제어 할 수 있습니다 (이제 광선 추적기와 같이 익숙한 기하학적 벡터에 대해 말하고 있습니다). . […]
15 September, 2022 at 9:17 am
Adversarial examples and quant quakes – Research Notebook
[…] in the data by diffusely spreading out across a large number of predictors. There’s a generalized uncertainty principle at work a la Donoho and Stark […]
7 March, 2023 at 4:33 pm
Anonymous
Dr Tao: You mentioned that the Poisson summation formula can be interpreted as a variant of the uncertainty principle using “adelic” topology. I don’t know anything about adelic topology. Could you explain a bit more about the interpretation? Thanks.